Анализ чувствительности

Анализ чувствительности – это наиболее простой путь количественного анализа рисков, чаще всего применяемый в практике анализа проектов. Он основан на последовательно-единичном изменении всех проверяемых на рискованность переменных: на каждом шаге только одна из переменных меняет свое значение на прогнозное число процентов, что приводит к пересчету значения используемого критерия. Целью его проведения является определение степени влияния каждого из варьируемых факторов на результат проекта. В отличие от предыдущего метода в качестве информационной основы используются данные потока денежных средств инвестиционного проекта. В качестве интегральных показателей, характеризующих результаты проекта, обычно рассматривают критерии проектной эффективности (NPV, IRR, РВР, PI). В ходе классического анализа чувствительности, применяемого к проекту, рассматривается последовательно-единичное влияние на конечный результат проекта (его эффективность) только одного варьируемого параметра (фактора, переменной), проверяемого на риск, при сохранении неизменными всех остальных параметров. Обычно при проведении анализа чувствительности выделяют две основных категории факторов по их влиянию:

на объем поступлений;

• на размеры затрат.

Кроме того, к факторам прямого воздействия относят:

• показатели инфляции;
• физический объем продаж на рынке;
• доля компании на рынке;
• потенциал роста и колебания рыночного спроса на продукцию;
• торговая цена и тенденции ее изменения;
• переменные издержки и тенденции их изменения;
• постоянные издержки и тенденции их изменения;
• требуемый объем инвестиций;
• стоимость привлекаемого капитала в зависимости от источников и условий его формирования.

В условиях высокой инфляции особо исследуются такие факторы, как факторы времени:

· длительность производственно-технологического цикла;

· время, затрачиваемое на реализацию готовой продукции;

· время, затрачиваемое на поступление денежных средств от реализации продукции (эффективность работы банковской системы, транспортные проблемы при оплате посредством аккредитива, взаимные неплатежи, условия реализации продукции (продажа в кредит и лизинг));

· договорное время задержки платежей;

· формирование и управление запасами (страховой запас готовой продукции на складе, страховой производственный запас сырья и материалов, динамически формируемый производственный запас);

· условия формирования капитала.

В России сейчас действуют два ограничения, которые необходимо учесть:

· дефицит акционерного капитала как следствие низкого уровня доходов населения и низкой привлекательности долгосрочных инвестиций;

· высокая стоимость заемного капитала, включая проценты по кредитам и затраты на обеспечение гарантий.

Применение анализа чувствительности и выбор варьируемых компонентов, влияющих на устойчивость проекта, безусловно, должны определяться для каждого конкретного проекта с учетом его специфики.

Анализ сценариев (Scenario analysis, What-If analysis)

Анализ сценариев позволяет исправить основной недостаток анализа чувствительности, так как включает одновременное (параллельное) изменение нескольких факторов риска и таким образом представляет собой развитие методики анализа чувствительности. В результате проведения анализа сценариев определяется воздействие на критерии проектной эффективности одновременного изменения всех основных переменных проекта, характеризующих его денежные потоки. Основным преимуществом метода является тот факт, что отклонения параметров рассчитываются с учетом их взаимозависимостей (корреляции). В качестве возможных вариантов при проведении риск-анализа целесообразно построить как минимум три сценария: пессимистический, оптимистический и наиболее вероятный (реалистический, или средний).

Главной проблемой практического использования сценарного подхода является необходимость построения модели инвестиционного проекта и выявление связи между переменными. Кроме того, к недостаткам сценарного подхода относят:

– необходимость значительного качественного исследования модели проекта, т.е. создания нескольких моделей, соответствующих каждому сценарию, включающих объемные подготовительные работы по отбору и аналитической переработке информации;

– достаточную неопределенность, «размытость» границ сценариев; правильность их построения зависит от качества построения модели и исходной информации, что значительно снижает их прогностическую ценность;

при построении оценок значений переменных для каждого сценария допускается некий волюнтаризм;

– эффект ограниченного числа возможных комбинаций переменных, заключенный в том, что количество сценариев, подлежащих детальной проработке ограничено, так же как и число переменных, подлежащих варьированию, в противном случае возможно получение чрезмерно большого объема информации, прогностическая сила и практическая ценность которой сильно снижаются.

Отметим, что для получения общего распределения последствий проекта, необходимо использовать имитационное моделирование.

Сценарный метод анализа проектных рисков обладает следующими особенностями, которые можно рассматривать в качестве его преимуществ:

1) учет взаимосвязи между переменными и влияния этой зависимости на значение интегрального показателя;

2)построение различных вариантов осуществления проекта;

3) содержательность процесса разработки сценариев и построения моделей, позволяющего проектному аналитику получить более четкое представление о проекте и возможностях его будущего осуществления, выявить как узкие места проекта, так и его позитивные стороны.

Таким образом, анализ чувствительности и сценарный анализ являются последовательными этапами количественного анализа рисков. Однако, метод сценариев наиболее эффективно применим в том случае, когда количество возможных значений NPV конечно. Вместе с тем, как правило, при проведении анализа рисков инвестиционного проекта эксперт сталкивается с неограниченным количеством различных вариантов развития событий. Метод количественной оценки риска конкретного инвестиционного проекта (имитационное моделирование) помогает разрешить отмеченную проблему.
В этом методе, который является одним из наиболее сложных в количественном анализе проектных рисков, активно используется математический аппарат теории вероятностей и математической статистики.
Так как при имитационном моделировании происходит имитация большого количества сценариев, то его можно назвать развитием сценарного подхода. Анализ значений результирующих показателей при сформулированных сценариях позволяет оценить возможный интервал их изменения при различных условиях реализации проекта. Использование вероятностных характеристик возможно для принятия инвестиционных решений, ранжирования проектов, обоснования применения тех или иных методов по управлению рисками проекта.

Применяя тот или иной метод анализа риска, следует иметь в виду, что кажущаяся высокая (особенно при использовании имитационного моделирования) точность результатов может быть обманчивой и ввести в заблуждение аналитиков и лиц, принимающих решение.

Value at Risk (Построение кривой риска)

VaR – это вероятностный подход, и основным понятием в нем является распределение вероятностей, связывающее все возможные величины изменений рыночных факторов с их вероятностями. Методология VaR обладает рядом несомненных преимуществ: она позволяет измерить риск в терминах возможных потерь, соотнесенных с вероятностями их возникновения; позволяет измерить риски на различных рынках универсальным образом; позволяет агрегировать риски отдельных позиций в единую величину для всего портфеля, учитывая при этом информацию о количестве позиций и периоде поддержания позиций.

Точное определение VaR формулируется следующим образом. Пусть фиксирован портфель. VaR портфеля для данного доверительного уровня p и данного периода поддержания позиций t определяется как такое значение V, которое обеспечивает покрытие возможных потерь x держателя портфеля за время t с вероятностью p, т.е. P(x ≤ V) = p.

Для вычисления VaR необходимо определить ряд базовых элементов, влияющих на его величину. В первую очередь это вероятностное распределение рыночных факторов, напрямую влияющих на изменение цен входящих в портфель активов. Понятно, что для его построения необходима некоторая статистика по поведению каждого из этих активов во времени. После задания распределения рыночных факторов необходимо выбрать доверительный уровень (confidence level), то есть вероятность, с которой наши потери не должны превышать VaR.

В отечественной литературе одно из проявлений использования метода VaR нашло отражении в построении кривой риска. Риск – это вероятностная категория, и в этом смысле наиболее обосновано характеризовать и измерять его как вероятность возникновения определенных потерь. При всесторонней оценке риска следовало бы устанавливать для каждого абсолютного или относительного значения величины возможных потерь соответствующую вероятность возникновения такой величины. Приведем схему зон риска (рис. 5).

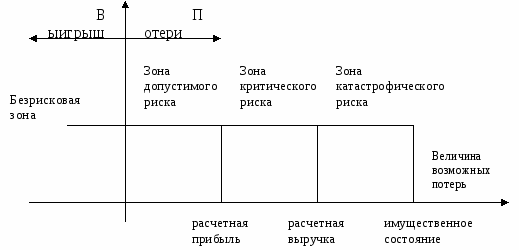
Рис.5. Схема зон риска

Построение кривой вероятностей (или таблицы) обычно становится исходной стадией оценки риска. Применительно к предпринимательству это чаще всего чрезвычайно сложная задача, поэтому практически приходится ограничиваться упрощенными подходами, оценивая риск по одному или нескольким показателям, представляющим обобщенные характеристики, наиболее важные для суждения о приемлемости риска. Рассмотрим некоторые из главных показателей риска. С этой целью сначала выделим основные области, или зоны риска в зависимости от величины потерь. Область, в которой потери не ожидаются, назовем безрисковой зоной, ей соответствуют нулевые или отрицательные потери (превышение прибыли).

Зоной допустимого риска представим область, в пределах которой данный вид предпринимательской деятельности сохраняет свою экономическую целесообразность, т.е. потери имеют место, но они меньше ожидаемой прибыли. Граница зоны допустимого риска соответствует уровню потерь, равному расчетной прибыли от предпринимательской деятельности.

Следующую, более опасную область назовем зоной критического риска. Это сфера, характеризуемая возможностью потерь, превышающих величину ожидаемой прибыли, вплоть до величины полной расчетной выручки от предпринимательства, представляющей сумму затрат и прибыли. Иначе говоря, зона критического риска характеризуется опасностью потерь, которые заведомо превышают ожидаемую прибыль и в максимуме могут привести к невозмещаемой потере всех средств, вложенных предпринимателем в дело. В последнем случае бизнесмен не только не получает от сделки никакого дохода, но несет убытки в сумме всех бесплодных затрат.

Кроме критического, реален катастрофический риск. Зона катастрофического риска представляет область потерь, которые по своей величине превосходят критический уровень и в максимуме могут достигать величины, равной имущественному состоянию предпринимателя. Катастрофический риск способен привести к краху, банкротству предприятия, его закрытию и распродаже имущества. К категории катастрофического относят вне зависимости от имущественного или денежного ущерба риск, связанный с прямой опасностью для жизни людей или возникновением экологических катастроф.

Наиболее полное представление о риске дает так называемая кривая распределения вероятностей потери, или графическое изображение зависимости вероятности потерь от их уровня, показывающее, насколько вероятно возникновение тех или иных потерь. Чтобы установить вид типичной кривой вероятности потерь, рассмотрим прибыль как случайную величину и построим вначале кривую распределения вероятностей получения определенного уровня прибыли (см. рис. 6).

При построении кривой распределения вероятностей получения прибыли приняты следующие предположения:

– наиболее вероятно получение прибыли, равной расчетной величине – ПР_р. Вероятность (В_р) получения такой прибыли максимальная, соответственно значение ПР_р можно считать математическим ожиданием прибыли. Вероятность получения прибыли, большей или меньшей по сравнению с расчетной, тем ниже, чем больше такая прибыль отличается от расчетной, т.е. значения вероятностей отклонения от расчетной прибыли монотонно убывают при росте отклонений;

– потерями прибыли считается ее уменьшение в сравнении с расчетной величиной ПР_р. Если реальная прибыль равна ПР, то потери прибыли равны ПР_р

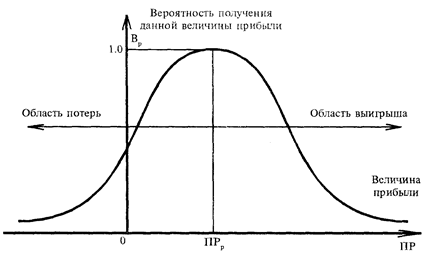
Рис. 6. Стандартная кривая вероятностей получения определенного уровня прибыли
Вероятность исключительно больших (теоретически бесконечных) потерь практически равна нулю, так как потери заведомо имеют верхний предел (исключая потери, которые не представляется возможным оценить количественно). Конечно, допущения в какой-то степени всегда спорны, ибо они могут не соблюдаться для всех видов риска. Но в целом они верно отражают общие закономерности изменения предпринимательского риска и базируются на гипотезе, что прибыль как случайная величина подчинена нормальному или близкому к нормальному закону распределения.

Исходя из кривой вероятностей получения прибыли, построим кривую распределения вероятностей возможных потерь прибыли, которую и следует называть кривой риска (фактически это та же кривая, но построенная в другой системе координат) (см. рис.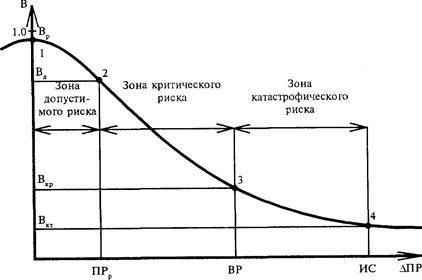

Рис. 7. Типичная кривая распределения вероятностей возникновения определенного уровня потерь прибыли

Выделим на изображенной кривой ряд характерных точек.

Первая точка определяет вероятность нулевых потерь прибыли. В соответствии с принятыми допущениями вероятность нулевых потерь максимальна, хотя, конечно, меньше единицы.

Вторая точка характеризуется величиной возможных потерь, равной ожидаемой прибыли, т.е. полной потери прибыли, вероятность которой равна В_д. Обе точки являются граничными, определяющими положение зоны допустимого риска.

Третья точка соответствует величине потерь, равных расчетной выручке ВР. Вероятность таких потерь равна В_кр. Точки 2 и 3 определяют границы зоны критического риска.

Четвертая точка характеризуется потерями, равными имущественному состоянию (ИС) предпринимателя, вероятность которой равна В_кт. Между точками 3 и 4 находится зона катастрофического риска.

Потери, превышающие имущественное состояние предпринимателя, не рассматриваются, так как их невозможно взыскать.

Вероятности определенных уровней потерь являются важными показателями, позволяющими высказывать суждение об ожидаемом риске и его приемлемости, поэтому построенную кривую и можно назвать кривой риска. Так, если вероятность катастрофической потери выражается показателем, свидетельствующим об ощутимой угрозе потери всего состояния, то осторожный предприниматель заведомо откажется от такого дела и не пойдет на подобный риск.

Если при оценке риска предпринимательской деятельности удается построить не всю кривую вероятностей риска, а только установить четыре характерные точки (наиболее вероятный уровень риска и вероятности допустимой, критической и катастрофической потери), то задачу такой оценки можно считать успешно решенной. Значения этих показателей в принципе достаточно, чтобы в подавляющем большинстве случаев идти на обоснованный риск.

Заметим, что предпринимателю, оценивающему риск, больше свойствен не точечный, а интервальный подход. Ему важно знать не только, что вероятность потерять 10000 руб. в намечаемой сделке составляет, скажем, 0,1 или 10 %. Он будет также интересоваться, насколько вероятно потерять сумму, лежащую в определенных пределах (в интервале, например, от 10000 до 15000 руб.). Наличие кривой вероятности потери позволяет ответить на такой вопрос путем нахождения среднего значения вероятности в заданном интервале потерь.

Вполне возможно и другое проявление интервального подхода в форме «полуинтервального», весьма характерного именно для предпринимательского риска.

В процессе принятия предпринимателем решений о допустимости и целесообразности риска ему важно представлять не столько вероятность определенного уровня потерь, сколько вероятность того, что потери не превысят некоторого уровня. По логике именно это и есть основной показатель риска. Вероятность того, что потери не превысят определенного уровня, есть показатель надежности, уверенности. Очевидно, что показатели риска и надежности предпринимательского дела тесно связаны между собой.

Предположим, предпринимателю удалось установить, что вероятность потерять 10000 руб. равна 0,1 %, т.е. относительно невелика, и он готов к такому риску. Принципиально важно здесь то, что предприниматель опасается потерять не ровно 10000 руб. Он готов идти на любую меньшую потерю и никак не готов согласиться на большую. Это естественная закономерная психология поведения предпринимателя в условиях риска.

Знание показателей риска – В_р, В_д, В_кр, В_кт – позволяет выработать суждение и принять решение о развертывании бизнеса. Но для такого решения недостаточно оценить значения показателей (вероятностей) допустимого, критического и катастрофического риска. Надо еще установить или принять предельные величины этих показателей, выше которых они не должны подниматься, чтобы не попасть в зону чрезмерного, неприемлемого риска.

Обозначим предельные значения вероятностей возникновения допустимого, критического и катастрофического риска соответственно К_д, К_кр, К_кт. Величины этих показателей в принципе должна устанавливать и рекомендовать теория предпринимательского риска, но обычно сам предприниматель назначает свои собственные предельные уровни риска, которые он не намерен превышать. Практика показывает, что можно ориентироваться на следующие предельные значения показателей риска:

К_д = 0,1; К_кр = 0,01; К_кт = 0,001, т.е. соответственно 10, 1, 0,1 %. Это означает, что не следует идти на предпринимательскую сделку, если в 10 случаях из ста можно потерять всю прибыль, в одном случае из ста потерять выручку и хотя бы в одном случае из тысячи потерять имущество.

В итоге, имея значения трех показателей риска и критериев предельного риска, можно сформулировать самые общие условия приемлемости анализируемого вида предпринимательства:

– показатель допустимого риска не должен превышать предельного значения (В_д < К_д);

– показатель критического риска должен быть меньше предельной величины (В_кр < К_д);

– показатель катастрофического риска не должен быть выше предельного уровня (В_кт < К_кт).

Таким образом, главное в оценке хозяйственного риска состоит в искусстве построения кривой вероятностей возможных потерь или хотя бы определении зон и показателей допустимого, критического и катастрофического риска.

Как уже было отмечено, основой применения метода VaR является верный выбор функции распределения. Существует три основных метода определения параметров функции распределения: исторический метод, аналитический и метод симуляции.

Исторический метод. Исторический метод заключается в исследовании изменения стоимости такого портфеля за предыдущий исторический период.
Для вычисления VaR составляется база данных за определенный исторический период значений цен инструментов, входящих в портфель. После этого надо вычислить изменения цен инструментов за промежуток времени, для которого рассчитывается VaR, и получить соответствующие значения изменения стоимости портфеля. Затем надо проранжировать полученные данные, построить гистограмму распределения изменений стоимости портфеля и найти значение VaR, соответствующее выбранному значению вероятности.

Преимущество данного метода состоит в том, что он свободен от предположений о виде распределения рыночных факторов портфеля, прост в осуществлении. При его использовании не возникает проблем с оценкой портфелей, содержащих опционы и подобные им инструменты.

К недостаткам метода следует отнести то, что он требует проведения большой работы по сбору исторических данных и их обработке. Кроме того, оценка возможных изменений стоимости портфеля ограничена набором предыдущих исторических изменений. Типичная проблема при использовании данного метода состоит в отсутствии требуемого количества исторических данных. Чтобы получить более точную оценку VaR, необходимо использовать как можно больше данных, но использование слишком старых данных приводит к тому, что сегодняшний риск будет оценен на основе данных, которые не соответствуют текущему состоянию рынка.

Аналитический метод. Основная идея метода заключается в выявлении рыночных факторов, влияющих на стоимость портфеля, и аппроксимации стоимости портфеля на основе этих факторов. То есть финансовые инструменты, составляющие портфель, разбиваются, насколько это возможно, на элементарные активы, такие, что изменения каждого зависит только от воздействия одного рыночного фактора.

Далее делается допущение о виде распределения рыночных факторов. Обычно считают, что доходность рыночных факторов подчиняется нормальному распределению. На основе исторических данных вычисляются математические ожидания, значения дисперсии и корреляции между факторами. Если аппроксимация имеет линейный вид, то распределение доходности портфеля также будет нормальным, и, зная параметры распределений рыночных факторов, можно определить параметры распределения всего портфеля. Серьезное преимущество этого подхода состоит в том, что для большинства рыночных факторов все необходимые параметры нормального распределения хорошо известны.

Оценка VaR, полученная с помощью аналитического метода, наиболее близко совпадает с оценкой риска, предлагаемой современной портфельной теорией. Данный метод позволяет очень быстро получать оценку VaR. Но качество оценки ухудшается при увеличении в портфеле доли инструментов с нелинейными функциями выплат. Кроме того, необходимость делать допущение о виде распределения для базовых активов является серьезным недостатком этого метода.

Метод симуляции (имитации)

Имитационное моделирование (simulation) является одним из мощнейших методов анализа экономических систем. В общем случае, под имитацией понимают процесс проведения на ЭВМ экспериментов с математическими моделями сложных систем реального мира. Цели проведения подобных экспериментов могут быть самыми различными – от выявления свойств и закономерностей исследуемой системы, до решения конкретных практических задач.

Как следует из определения, имитация – это компьютерный эксперимент. Единственное отличие подобного эксперимента от реального состоит в том, что он проводится с моделью системы, а не с самой системой. Однако проведение реальных экспериментов с экономическими системами, по крайней мере, неразумно, требует значительных затрат и вряд ли осуществимо на практике. Таким образом, имитация является единственным способом исследования систем без осуществления реальных экспериментов.

В общем случае, проведение имитационного эксперимента можно разбить на следующие этапы:

1. Установить взаимосвязи между исходными и выходными показателями в виде математического уравнения или неравенства.

2. Задать законы распределения вероятностей для ключевых параметров модели.

3. Провести компьютерную имитацию значений ключевых параметров модели.

4. Рассчитать основные характеристики распределений исходных и выходных показателей.

5. Провести анализ полученных результатов и принять решение.

Результаты имитационного эксперимента могут быть дополнены статистическим анализом, а также использоваться для построения прогнозных моделей и сценариев.

При решении многих задач финансового анализа используются модели, содержащие случайные величины, поведение которых не поддается управлению со стороны лиц, принимающих решения. Такие модели называют стохастическими.
К стохастической имитации относят метод Монте-Карло.

Имитационное моделирование по методу Монте-Карло (Monte-Carlo Simulation) позволяет построить математическую модель для проекта с неопределенными значениями параметров, а также, зная вероятностные распределения параметров проекта и связь между изменениями параметров (корреляцию), получить распределение доходности проекта.

Данный метод заключается в моделировании возможных изменений стоимости портфеля при некоторых предположениях. Выявляются основные рыночные факторы, влияющие на стоимость портфеля. Затем строится совместное распределение этих факторов каким-либо способом, например, с использованием исторических данных или данных, основанных на каком-либо сценарии развития экономики, для чего определяются функции распределения каждой переменной, оказывающей влияние на формирование потока наличности. Как правило, предполагается, что функция распределения являются нормальной, и, следовательно, для того, чтобы задать ее, необходимо определить только два момента (математическое ожидание и дисперсию).

Как только функция распределения определена, можно применять процедуру Монте-Карло.

Алгоритм метода имитации Монте-Карло

Шаг 1. Опираясь на использование статистического пакета, и основываясь на вероятностной функции распределения, случайным образом выбираем, значение переменной, которая является одним из параметров определения потока наличности.

Шаг 2. Выбранное значение случайной величины наряду со значениями переменных, которые являются экзогенными переменными используется при подсчете чистой приведенной стоимости проекта.

Шаги 1 и 2 повторяются большое количество раз, например 1000, и полученные 1000 значений чистой приведенной стоимости проекта используются для построения плотности распределения величины чистой приведенной стоимости со своим собственным математическим ожиданием и стандартным отклонением.

Используя значения математического ожидания и стандартного отклонения, можно вычислить коэффициент вариации чистой приведенной стоимости проекта и затем оценить индивидуальный риск проекта, как и в анализе методом сценариев.

Теперь необходимо определить минимальное и максимальное значения критической переменной, а для переменной с пошаговым распределением помимо этих двух еще и остальные значения, принимаемые ею. Границы варьирования переменной определяются просто исходя из всего спектра возможных значений.

По прошлым наблюдениям за переменной можно установить частоту , с которой та принимает соответствующие значения. В этом случае вероятностное распределение есть то же самое частотное распределение, показывающее частоту встречаемости значения, правда, в относительном масштабе (от 0 до 1). Вероятностное распределение регулирует вероятность выбора значений из определенного интервала. В соответствии с заданным распределением модель оценки рисков будет выбирать произвольные значения переменной. До рассмотрения рисков мы подразумевали, что переменная принимает одно определенное нами значение с вероятностью 1. И через единственную итерацию расчетов мы получали однозначно определенный результат. В рамках модели вероятностного анализа рисков проводится большое число итераций, позволяющих установить, как ведет себя результативный показатель (в каких пределах колеблется, как распределен) при подстановке в модель различных значений переменной в соответствии с заданным распределением.

Задача аналитика, занимающегося анализом риска, состоит в том, чтобы хотя бы приблизительно определить для исследуемой переменной (фактора) вид вероятностного распределения. При этом основные вероятностные распределения, используемые в анализе рисков, могут быть следующими: нормальное, постоянное, треугольное, пошаговое. Эксперт присваивает переменной вероятностное распределение исходя из своих количественных ожиданий и делает выбор из двух категорий распределений: симметричных (например, нормальное, постоянное, треугольное) и несимметричных (например, пошаговое распределение).

Существование коррелированных переменных в проектном анализе вызывает порой проблему, не рассмотреть которую означало бы заранее обречь себя на неверные результаты. Ведь без учета коррелированности, скажем, двух переменных – компьютер, посчитав их полностью независимыми, генерирует нереалистичные проектные сценарии. Допустим, цена и количество проданного продукта есть две отрицательно коррелированные переменные. Если не будет уточнена связь между переменными (коэффициент корреляции), то возможны сценарии, случайно вырабатываемые компьютером, где цена и количество проданной продукции будут вместе либо высоки, либо низки, что, естественно, негативно отразится на результате.

Проведение расчетных итераций является полностью компьютеризированной частью анализа рисков проекта. 200–500 итераций обычно достаточно для хорошей репрезентативной выборки. В процессе каждой итерации происходит случайный выбор значений ключевых переменных из специфицированного интервала в соответствии с вероятностными распределениями и условиями корреляции. Затем рассчитываются и сохраняются результативные показатели (например, NPV). И так далее, от итерации к итерации.

После этого моделируется большое число возможных сценариев развития ситуации, и изменение портфеля считается для каждого результата моделирования. Далее строится гистограмма полученных данных и определяется значение VaR.

Этот метод имеет несколько преимуществ. Он не использует конкретную модель определения параметров и может быть легко перенастроен в соответствии с экономическим прогнозом. Метод моделирует не конечную стоимость портфеля, а целый сценарий развития ситуации, что позволяет отслеживать изменение стоимости портфеля в зависимости от пути развития ситуации.
Недостаток метода – его медленная сходимость, что приводит к существенным временным и вычислительным затратам.

Выше упоминались достоинства метода VaR как метода количественной оценки риска, однако этот метод наряду с выраженными преимуществами также имеет и недостатки. Общий недостаток VaR заключается в том, что все модели VaR независимо от применяемых методов вычисления используют исторические данные. И если условия на рынке резко меняются, например, скачкообразно изменяется волатильность рынка или изменяется корреляция между активами, то VaR учтет эти изменения только через определенный промежуток времени. А до этого момента оценка VaR будет некорректна.

При оценке VaR не учитывается такая важная характеристика рынков, как ликвидность. Это может привести к тому, что в определенные моменты изменение структуры портфеля для уменьшения риска может оказаться затруднительным.

VaR оценивает вероятность возникновения потерь больше определенного уровня, то есть оценивает «вес хвоста» распределения, но ничего не говорит о том, насколько велики могут быть эти потери. Поэтому дополнительно к VaR рекомендуется изучать поведение портфеля в стрессовых ситуациях, чтобы оценить «длину хвоста» распределения.

Все эти факторы приводят к тому, что VaR хорошо работает в случае стабильного состояния на рынках и перестает адекватно отображать величину риска, если на рынках происходят драматические изменения. Следует помнить, что VaR – всего лишь один из инструментов при управлении риском, а не универсальный способ его оценки.