Взаимосвязь продуктовых инноваций и структуры отраслевого рынка
Научно-исследовательские и опытно-конструкторские разработки
Инновации
Инновации – это нововведения, направленные на улучшение деятельности предприятия или выпускаемой им продукции.
В теории принято выделять следующие виды инноваций:
1) производственные;
2) маркетинговые;
3) управленческие.
Производственные инновации в свою очередь делятся на технологические и продуктовые.
Технологические инновации имеют своим результатом снижение себестоимости производства продукции, более эффективное использование дефицитных ресурсов, ускорение сроков производства и т.д. Таким образом, при внедрении технологической инновации повышается производственная эффективность предприятия, снижается величина минимального эффективного выпуска продукции, улучшается конкурентное положение предприятия на рынке.
Продуктовые инновации имеют целью расширение спроса на продукцию предприятия через улучшение потребительских характеристик выпускаемой продукции, разработку и внедрение новых видов продукции.
Маркетинговые инновации состоит в разработке и внедрении новых методов воздействия на предпочтения потребителей, расширения рынков сбыта, повышения эффективности продвижения продукции на рынок.
Управленческие инновации направлены на повышение эффективности бизнес-процессов и управления компанией.
На структуру отраслевых рынков влияние оказывают в первую очередь производственные инновации, так как в результате них предприятия получают длительные конкурентные преимущества перед другими предприятиями отрасли. При этом необходимо отметить, что производственные инновации, как правило, защищены патентным законодательством и политикой компанией по защите интеллектуальной собственности, по этой причине конкурентам их достаточно трудно скопировать. В то же время маркетинговые и управленческие инновации могут быть скопированы достаточно быстро и без особых затрат. По этой причине влияние на структуру отраслевого рынка маркетинговых и управленческих инноваций является кратковременным.
В этой связи при анализе влияния инноваций на отраслевой рынок ограничиваются преимущественно анализом технологических и продуктовых инноваций.
Необходимо отметить, что разные инновации могут обладать разной эффективностью. Так, в условиях высокого платежеспособного спроса и больших темпов роста рынка большей эффективностью обладают, как правило, продуктовые инновации. В то же самое время в отраслях, вступивших в фазу зрелости и насыщения спроса, более эффективными могут оказаться технологические инновации. К примеру, в США в 1990-е годы отношение расходов на разработку продуктовых инноваций к расходам на технологические инновации составляло 3 к 1.
Важным вопросом при исследовании инноваций является взаимосвязь инновационной активности компаний с особенностями отраслевых рынков. Эмпирические исследования показывают, что наиболее высокий уровень расходов на НИОКР имеется в отраслях с высокой концентрацией производства и наличием монопольной власти. Данные результаты согласуются с так называемой гипотезой Йозефа Шумпетера.
Гипотеза Й. Шумпетера: экономическая прибыль, аккумулируемая предприятиями с монопольной властью, является основным источником финансирования дорогостоящих и рискованных инноваций в условиях нестабильности рыночной структуры, обусловленной технологическими изменениями, а стимулом к осуществлению инноваций является стремление к увеличению монопольной власти.
В качестве объяснения этого можно привести такой довод, что на инновации расходуется преимущественно сверхприбыль компаний. Кроме того, необходимо отметить, что активная инновационная деятельность позволяет компании вести жесткую конкурентную борьбу и удерживать позицию на рынке.
На практике, проверить истинность гипотезы Й. Шумпетера затруднительно, вследствие сложностей в разграничении влияния образующейся экономической прибыли на инновационную активность и влияния инновационной активности на образование экономической прибыли. Вместе с тем не всегда наличие монопольной прибыли является обязательным условием для осуществления инноваций, в качестве примера можно привести отрасль венчурного финансирования, деятельность которой строится на основе осуществления прямых инвестиций, позволяющих целевым предприятиям проводить активную инновационную политику и, в случае удачи последней, получать экономическую прибыль.
Таким образом, инновационная политика является важной составляющей конкурентной стратегии предприятия. Рассмотрим далее основные модели, позволяющие анализировать связь между расходами на НИОКР и отраслевой структурой.
Модели инноваций
Рассмотрим однопериодные модели инноваций в условиях олигополии. Однопериодная модель олигополистической структуры предполагает, что фирмы одновременно принимают решения по поводу уровня расходов на НИОКР. Таким образом, мы имеем дело с моделью Нэша-Курно, в которой в качестве стратегических переменных выступают объем производства продукции и объем расходов на НИОКР.
Вначале рассмотрим конкуренцию в области технологических инноваций. Исторически первая модель олигополии с конкуренцией в области технологических инноваций была предложена американскими экономистами Дасгупте и Стиглицом в 1980 г.
Модель олигополии с конкуренцией в области технологических инноваций (Дасгупте, Стиглиц, 1980 г.)
Пусть отрасль, состоящая из n фирм, приступает к производству нового продукта. Обратная кривая рыночного спроса выражается функцией P(Q), где Q – совокупный выпуск фирм.
qi – выпуск фирмы i, i = 1,…,n;
c(xi)– затраты на единицу продукции для фирмы i, i = 1,…,n;
xi – расходы фирмы i на инновации, i = 1,…,n.
Пусть для простоты у фирм не существует иных постоянных затрат, кроме xi. В этом случае функция прибыли фирмы iбудет иметь следующий вид:
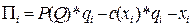
Фирма будет максимизировать прибыль на множестве допустимых значений xi и qi. Как уже было отмечено выше, в однопериодной модели мы полагаем, что конкуренты будут вести себя в соответствии с моделью Нэша-Курно. В результате мы получаем следующие два условия первого порядка для равновесия:
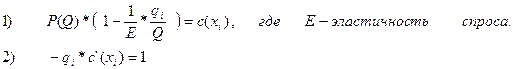
Первое условие представляет собой обычное условие равенства предельной выручки предельным затратам. А второе означает, что в состоянии равновесия функция c(xi)должна показывать убывающую отдачу от масштаба. Следовательно, фирма должна продолжать инвестировать в инновации до тех пор пока предельная отдача от них (объем выпуска, помноженный на снижение себестоимости) не станет равной единичной стоимости дальнейших расходов на инновации.
Если мы предположим, что все фирмы в отрасли одинаковы, то данные условия примут следующий вид:

Далее Дасгупта и Стиглиц предприняли попытку проанализировать данную дифференциальную характеристику равновесия при предположении, что число фирм может меняться. Анализ полученных равновесных величин дал следующие результаты:
1. Как и в простой модели Курно, общий выпуск растет при увеличении числа фирм, хотя каждая фирма производит меньший объем, получая при этом меньшую прибыль.
2. С ростом числа фирм, каждая фирма производит меньше продукции, а следовательно, имеет меньший эффект от увеличения технологических инноваций (эффект снижения издержек распространяется на меньший объем производства), в результате чего каждая фирма тратит меньше на инновации и, как следствие, удельные затраты на производство (c(x)) возрастают[1].
Полученные результаты поднимают естественный вопрос, как под воздействием конкуренции в области технологических инноваций меняется общественное благосостояние. Как мы видим увеличение числа фирм, а следовательно, и конкурентности рынка, ведет к увеличению отраслевых объемов производства, однако увеличение объемов производства достигается при больших удельных издержках, вследствие этого эффект воздействия на общественное благосостояние не определен.
Рассмотрение долгосрочного равновесия в рамках данной модели Дасгупте и Стиглиц провели при стандартных предположениях о свободе входа и выхода и равенства нулю экономической прибыли, что может быть записано следующим уравнением:

В состоянии симметричного равновесия, при предположении, что n* фирм точно могут получать прибыль, это условие будет выглядеть следующим образом:
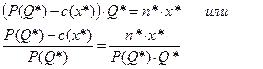
То есть разница между ценой и удельными издержками производства целиком поглощается расходами на инновации.
В таком случае, учитывая, что 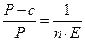 , мы можем записать:
, мы можем записать: 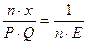
Где левая часть представляет собой долю отраслевых затрат на технологические инновации в общей выручки от реализации продукции.
Таким образом, доля расходов на НИОКР в общей выручке отрасли находится в обратной зависимости от числа фирм в отрасли и эластичности выпуска по цене, а следовательно увеличение числа фирм на рынке и снижение монопольной власти ведет к снижению стимулов к осуществлению инноваций, что согласуется с гипотезой Й. Шумпетера.
Рассмотрим далее однопериодную модель продуктовой инновации.
Модель олигополии с конкуренцией в области продуктовых инноваций (Дорфман, Штайнер, 1954 г.)
В данном случае мы имеем дело уже с монополистической конкуренцией, поскольку продуктовая инновация ведет к изменению потребительских характеристик продукции, что сопровождается, как правило, появлением новой торговой марки на рынке. Так как продуктовые инновации направлены на улучшение продукта, то остаточный спрос на продукцию произвольной фирмы i (qi) будет зависеть от величины расходов на продуктовые инновации и цен на продукцию, как самой фирмы i, так и ее конкурентов:
 ,
,
где
Pi – цена на продукцию фирмы i;
xi– расходы на продуктовые инновации фирмы i;
P-i и x-i – цены на продукцию и расходы на продуктовые инновации конкурентов фирмы i.
Так как продуктовые инновации способствуют росту остаточного спроса, то можно предположить, что рост расходов на продуктовые инновации ведет к расширению остаточного спроса (  ), однако по мере увеличения расходов на инновации эффект расширения спроса будет ослабевать.
), однако по мере увеличения расходов на инновации эффект расширения спроса будет ослабевать.
В таком случае фирма будет стремиться максимизировать прибыль (Пi), выбирая соответствующие цены (Pi), и уровень расходов на продуктовые инновации (xi):
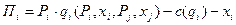
Откуда первое условие оптимальности:
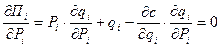
или, в терминах эластичности:
 .
.
Второе условие оптимальности имеет вид:
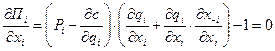
или в терминах эластичностей:
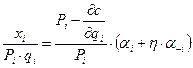 , где
, где
αi – эластичность объема продаж по расходам на продуктовые инновации;
α-i – эластичность объема продаж по расходам на продуктовые инновации других фирм;
η – степень ожидаемого роста расходов на продуктовые инновации конкурентов фирмы i в ответ на увеличение этих расходов данной фирмой.
Таким образом, доля расходов на продуктовые инновации в валовой выручке от реализации продукции прямо пропорциональна эластичности объема продаж по расходам на продуктовые инновации и обратно пропорциональна прямой эластичности спроса по цене.
Заметим, что в однопериодной модели член η равен нулю, что приводит к равновесию по Нэшу.
Рост числа фирм в рамках такой модели, так же как и в случае технологических инноваций, снижает стимулы к продуктовых инновациям. Более того, рассмотрение многопериодной модели показывает, что фирмам выгоден сговор, удерживающий их от инновационной гонки.
Дальнейшее развитие моделей, включающих расходы на инновации, ведет к построению динамических моделей. В связи с этим делаются следующие предположения.
1. Конкуренция в сфере НИОКР ведет к появлению выигравших и проигравших. При этом преимущество победителя закрепляется либо патентом, либо засекречиванием информации, либо через эффективное блокирование входа на рынок.
2. В конкурентной борьбе в сфере НИОКР имеется существенная неопределенность, в результате которой невозможно точно установить какая фирма окажется лидером в инновациях.
3. Между фирмами существует асимметрия. Некоторые из них только пытаются войти на рынок, в то время как другие владеют патентами на изобретения и т.д.
На практике учесть все три условия в одной модели достаточно сложно, поэтому исследователи предпочитают отказываться от некоторых из них.
Проанализировав базовые модели инновационной конкуренции, перейдем к выявлению взаимосвязей между структурой рынка и продуктовыми инновациями.
Взаимосвязь продуктовых инноваций и структуры отраслевого рынка
Введение продуктовой инновации можно рассматривать как вход на рынок с некоторым потенциалом получения прибыли. В этой связи возникает понятие квазиренты, образующейся в результате получения фирмой положительной экономической прибыли, вызванной внедрением инновации. Продолжительность получения квазиренты зависит от многих факторов, в том числе от отраслевой специфики, степени защищенности инновации и т.д. Как правило, квазирента обладает достаточно длительным потенциалом. В случае если спрос на данную продукцию не зависит от факторов спроса на другие товары (случай совершенной монополии), то квазирента представляет собой постоянный бесконечный аннуитет. Если же рынок характеризуется монополистической конкуренцией, то размер квазиренты, при прочих равных условиях, будет постепенно возрастать со временем, по мере переключения потребителей на потребление более совершенной продукции, предложенной на рынке.
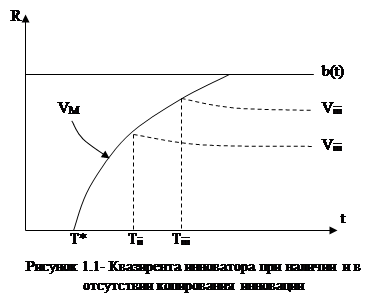
Кратко проанализируем, как происходит образование квазиренты. При отсутствии каких-либо субсидий фирма-инноватор не может получить прибыль до тех пор, пока НИОКР не будут закончены и новая продукция не будет предложена покупателям. Обозначим такую дату внедрения как Т*(см. рис. 1.1). Тогда квазирентный потенциал нового продукта, ежегодная прибыль инноватора, будет постепенно возрастать до того момента, когда инноватор полностью не монополизирует рынок (линия VM).
Однако, как бы инноватор не пытался защитить свое нововведение (например, путем патентования), это не устраняет вероятности копирования его инновации конкурентами.
Предположим, что один из конкурентов имитирует данный продукт в момент Tii. В этом случае этому конкуренту начинает доставаться часть квазиренты, которая бы доставалась инноватору в условиях отсутствия копирования, а квазирента, получаемая инноватором, становится Vii. Расстояние между VM и Vii представляет собой квазиренту, полученную конкурентом, которому удалось скопировать продукт, при предположении об отсутствии ценовой конкуренции между ним и инноватором. Рассмотрим теперь ситуацию, когда конкурентам удалось скопировать новый продукт в момент Тiii большем чем Tii. В этом случае, как мы видим из рис. 8.1 квазирента, полученная инноватором, будет больше (Viii), а квазирента, полученная конкурентами, которым удалось скопировать продукт, будет меньше. Таким образом, инноватору выгоднее всячески предотвращать вход конкурентов на рынок нового продукта.
Вместе с тем остался еще один не рассмотренный вопрос – что определяет положение Т*?
Для ответа на данный вопрос мы должны построить и рассмотреть модель максимизации прибыли инноватора. Рассмотрим данную модель на рис. 1.2. Предположим, что в момент принятия решения инноватор находится в момент Т = 0.
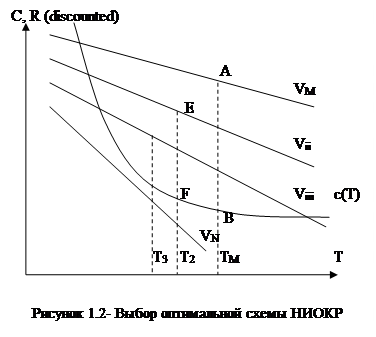 Пусть с(Т) – условная функция издержек инноватора, показывающая объем общих затрат инноватора на НИОКР, необходимых для ввода на рынок новой продукции в период Т. Представленный вид функции с(Т) отражает тот факт, что для достижения более ранних сроков внедрения инновации необходимы более высокие дисконтированные затраты на НИОКР. Ускорение темпов НИОКР увеличивает расходы по трем причинам: 1) необходимо проводить большее число параллельных проектов НИОКР, чтобы достичь успеха в условиях неопределенности в сжатые сроки; 2) увеличивается вероятность неудачных стартов производства новой продукции; и 3) уменьшается отдача при распределении талантливых разработчиков между проектами НИОКР, а привлечение новых сотрудников сопровождается увеличением стоимости персонала. Линия VM отражает дисконтированную стоимость монопольной квазиренты (при монопольном положении на рынке нового продукта), ожидаемой инноватором в будущем при условии, что продукция появляется на рынке в момент Т. Величина этой квазиренты тем меньше, чем дольше период от принятия решения об инвестировании в НИОКР до появления новой продукции на рынке. В этих условиях, если предприятие не ожидает конкуренции со стороны имитаторов инновации, задача максимизации прибыли сводится к поиску наибольшего расстояния между VM и с(Т). Это соответствует запуску производства новой продукции в момент ТМ.
Пусть с(Т) – условная функция издержек инноватора, показывающая объем общих затрат инноватора на НИОКР, необходимых для ввода на рынок новой продукции в период Т. Представленный вид функции с(Т) отражает тот факт, что для достижения более ранних сроков внедрения инновации необходимы более высокие дисконтированные затраты на НИОКР. Ускорение темпов НИОКР увеличивает расходы по трем причинам: 1) необходимо проводить большее число параллельных проектов НИОКР, чтобы достичь успеха в условиях неопределенности в сжатые сроки; 2) увеличивается вероятность неудачных стартов производства новой продукции; и 3) уменьшается отдача при распределении талантливых разработчиков между проектами НИОКР, а привлечение новых сотрудников сопровождается увеличением стоимости персонала. Линия VM отражает дисконтированную стоимость монопольной квазиренты (при монопольном положении на рынке нового продукта), ожидаемой инноватором в будущем при условии, что продукция появляется на рынке в момент Т. Величина этой квазиренты тем меньше, чем дольше период от принятия решения об инвестировании в НИОКР до появления новой продукции на рынке. В этих условиях, если предприятие не ожидает конкуренции со стороны имитаторов инновации, задача максимизации прибыли сводится к поиску наибольшего расстояния между VM и с(Т). Это соответствует запуску производства новой продукции в момент ТМ.
Предположим теперь, что у инноватора имеется конкурент на рынке нового продукта. Если речь идет о фирме, копирующей новый продукт, то при выходе на рынок, эта фирм столкнется с неравномерным распределением квазиренты: большая часть квазиренты, возникающей в результате инновации, будет доставаться инноватору (Vii). В этой связи разумно предположить, что если бы фирма-конкурент была в равных с инноватором начальных условиях, то вряд ли она согласилась бы на роль аутсайдера в инновационной конкуренции. Таким образом, в случае олигополистической структуры мы будем иметь дело с конкуренцией по Курно. При наличии конкуренции линия дисконтированной квазиренты для инноватора поворачивается по часовой стрелке и смещается вниз. При более крутом наклоне наибольшее расстояние между Vii и с(Т) достигается при Т2 меньшем чем ТМ.
Таким образом, наличие конкуренции на рынке данного товара приводит к сокращению эффективного срока НИОКР, а также сокращению получаемой в результате внедрения квазиренты, как для предприятия-инноватора, так и для всей отрасли в целом.
Рассмотрев ситуацию симметричного положения фирм на рынке, рассмотрим, что происходит в случае, если фирмы имеют разное положение на рынке. Анализ такой ситуации показывает, что более крупные фирмы имеют меньше стимулов для ускорения темпов НИОКР, в то время как мелкие фирмы заинтересованы в более раннем внедрении инновации, благодаря чему они существенно расширяют свою долю рынка. Предлагается самим проанализировать данную ситуацию.
Чем более симметричными будут фирмы, тем более крутым будет наклон функции дисконтированной квазиренты типичной фирмы (так, функция Viii (в случае трех симметричных фирм) имеет более крутой наклон, чем функция Vii). Чем круче наклон, тем быстрее фирмы стремятся произвести НИОКР. Таким образом, рост числа симметричных фирм, с одной стороны ускоряет темпы НИОКР, а с другой стороны, сокращает суммарную величину квазиренты.
Однако, существует предел роста числа симметричных фирм, это такое число N, при котором линия дисконтированной квазиренты начинает проходить ниже линии затрат на НИОКР. Если НИОКР должны осуществляться в любом случае, то они при любом периоде исследований приведут к убыткам для фирм. В результате это приведет к провалу рынка – каждая фирма будет воздерживаться от инвестиций в НИОКР, предполагая, что если все фирмы также начнут осуществлять НИОКР, то выгоды от внедрения инновации не возместят расходов на НИОКР.
Здесь имеется и другая проблема. По мере роста числа фирм, усиливаются возможности ценовой конкуренции, что, в свою очередь, приводит к сокращению ожидаемой прибыли.
[1] Этот результат является следствием допущений, принятых в модели. Так, к примеру, Са (Sah) и Стиглиц позже предложили модель, в которой продуктовый рынок характеризуется конкуренцией по Бертрану, так что фирма получает отдачу от НИОКР только тогда, когда она является единственным инноватором; если же инновации создаются двумя фирмами, то конкуренция между ними сводит прибыль обеих к нулю. Продолжая цепь рассуждений, они пришли к выводу, что расходы на НИОКР не зависят от числа фирма в отрасли.
| <== предыдущая лекция | | | следующая лекция ==> |
| Представление чисел в ЭВМ. | | | УЛУЧШЕНИЕ УСЛОВИЙ ЛОВА РЫБЫ |
Дата добавления: 2016-10-17; просмотров: 1854;
