МИНОРЫ И АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ ОПРЕДЕЛИТЕЛЕЙ.

Минором любого элемента определителя называется, определитель второго

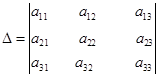
порядка, полученный вычеркиванием из данного определителя строки и столбца, содержащих этот элемент. Так минор для элемента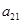

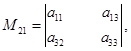
для элемента :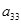

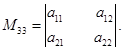
Алгебраическим дополнением любого элемента определителя называют минор этого элемента взятый с множителем 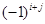, где i – номер строки элемента, j – номер столбца. Таким образом, алгебраическое дополнение элемента :

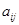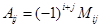
Пример. Найти алгебраические дополнения 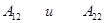для элементов определителя.

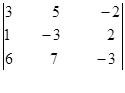
Теорема. Определитель равен сумме произведений элементов любого его столбца или строки на их алгебраические дополнения.

Другими словами, имеют место следующие равенства для определителя .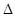

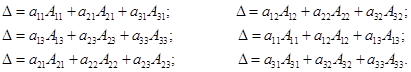
Доказательство этих равенств состоит из замены алгебраических дополнений их выражениями через элементы определителя, при этом получим выражение (3). Предлагается это выполнить самостоятельно. Замена определителя 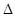по одной из шести формул называется разложением определителя 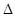по элементам соответствующего столбца или строки. Эти разложения применяют для вычисления определителей.

Пример. Вычислить определитель, разложив его по элементам второго столбца.

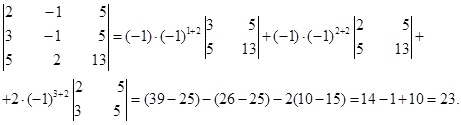
Используя теорему о разложении определителя третьего порядка по элементам строки или столбца, можно доказать справедливость свойств 1-8 для определителей третьего порядка. Предполагается проверить справедливость этого утверждения. Свойства определителей и теорема о разложении определителя по элементам столбца или строки позволяют упростить вычисления определителей.

Пример. Вычислить определитель.

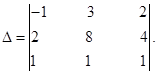
Вычислим общий множитель «2» элементов второй строки, а затем такой же общий множитель элементов третьего столбца.

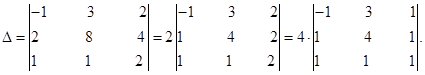
Прибавим элементы первой строки к соответствующим элементам второй строки, затем третьей строки.

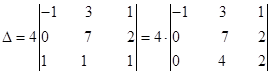
Разложим определитель по элементам первого столбца:

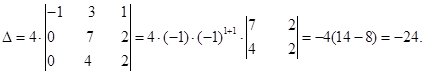
Полезным является следующее утверждение: сумма произведений элементов какого-либо столбца (или строки) на алгебраические дополнения элементов какого-либо другого столбца (или строки) равна нулю, т.е. имеют место равенства:

Каждое из этих равенств представляет собой разложение определителя по элементам столбца (или строки), у которого одинаковы элементы столбцов (или строк).