Исходные данные для анализа риска вложений в акции компании А и С
Рассчитаем наиболее вероятную доходность для акции А:
KB = 10% ´ 0,2 + 14% ´ 0,5 + 18% ´ 0,2 + 24% ´ 0,1 = 15%.
Стандартное отклонение от наиболее вероятной доходности для акций А составит:
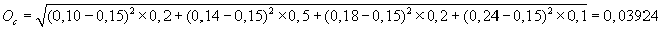или 3,92%.
Коэффициент вариации составит:
V = 3,92% : 15% = 0,2616, или 26,16%.
Повторим аналогичные расчеты для акций компании С:
KB = 16% ´ 0,1 + 22% ´ 0,3 + 29% ´ 0,5 + 32% ´ 0,1 = 25,9%;
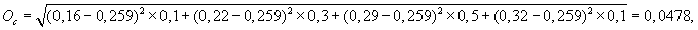или 4,78%;
V = 4,78% : 25,9% = 0,1846, или 18,46%.
Таким образом, коэффициент вариации для акций А выше, чем для акций С, что означает более высокую степень риска для инвестора.
Доход, обеспечиваемый вложениями в ценную бумагу, состоит из двух частей: дохода от изменения стоимости ценной бумаги (прироста капитала) и текущего дохода (дивиденда, процента), выплачиваемого с определенной периодичностью.
Такое разделение видов дохода по ценной бумаге дает нам возможность рассчитать различные виды доходности. По акциям можно рассчитать следующие виды доходности: ставка дивиденда, текущая доходность, конечная доходность:
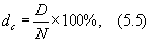
где dc ¾ ставка дивиденда, %;
D ¾ величина годового дивиденда, д. е.;
N ¾ номинальная цена акции, д. е.;
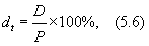
где dt ¾ текущая доходность акции, %;
P ¾ текущая рыночная цена акции, д. е.;
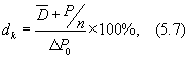
где dk ¾ конечная доходность акции, %;
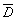¾среднегодовой дивиденд, д. е.;
DР ¾ разница между ценой продажи и ценой покупки акции, д. е.;
Р0 ¾ цена покупки акции, д. е.;
n ¾ число лет от покупки до продажи акции.
Пример.
Инвестор купил акцию номиналом 100 д. е. с коэффициентом 1,7. В первый год дивиденд по акции составил 15 д. е. Во второй год рендит (текущая доходность) оценивался в 20% годовых; в третий год ставка дивиденда составила 45% годовых. Дивиденды выплачивались равномерно по кварталам. Инвестор продал акцию на третий год после приобретения за 90 дней до выплаты годовых дивидендов. Индекс динамики цены продажи по отношению к цене покупки составил 1,25.
Рассчитайте конечную доходность акции.
Предварительно рассчитаем цены покупки и продажи акции:
P0 = 100 руб. ´ 1,7 = 170 д. е.,
P1 = 170 руб. ´ 1,25 = 212,5 д. е.
Определим текущие доходы инвестора.
Дивиденд за первый год известен: D1 = 15 д. е.
Так как текущая доходность за второй год составила 20%, то:
D2 = 170 д. е. ´ 0,2 = 34 д. е.
Так как ставка дивиденда за третий год была равна 45% годовых и инвестор получил дивиденды только за три квартала, то:
D3 = 100 руб. ´ 0,45 ´ 0,75 = 37,5 д. е.
Среднегодовой дивиденд составил:
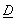=(15 д. е. +34 д. е. +37,5 д. е.) : 2,75 =31,45 д. е.
Кроме текущих доходов инвестор получил приращение капитала в виде разницы между ценой продажи и ценой покупки акции:
P1 - P0 = 212,5 д. е. - 170 д. е. = 42,5 д. е.
Подставляя все найденные величины в формулу конечной доходности (5.7), получим:
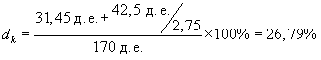
Экономическое значение полученного результата можно интерпретировать следующим образом: на каждый рубль, вложенный в данную акцию, инвестор получал в среднем за год около 27 коп. прибыли (без учета налогообложения).
По облигациям можно рассчитать следующие виды доходности: купонная, текущая доходность, доходность до погашения:
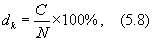
где dk ¾ купонная доходность, %;
С ¾ величина годового купонного дохода, д. е.;
N ¾ номинальная цена облигации, д. е.;
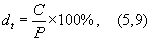
где dt ¾ текущая доходность облигации, %;
Р ¾ текущая рыночная цена облигации, д. е.;
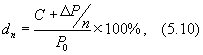
где dn ¾ доходность до погашения, %;
DР ¾ разница между ценой продажи (погашения) и ценой покупки облигации, д. е.;
Р0 ¾ цена покупки облигации, д. е.;
n ¾ число лет от покупки до продажи (погашения) облигации.
Пример.
Облигация с купоном 20% годовых и сроком обращения три года имеет рыночный курс 40%.
Определите текущую доходность и доходность до погашения данной облигации:
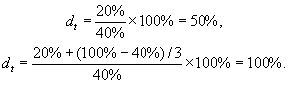
Согласно фундаментальному анализу текущая рыночная стоимость (Vm) ценной бумаги определяется как совокупный денежный поток, генерируемый данной ценной бумагой, приведенный к настоящему моменту времени, и может быть рассчитана по формуле:
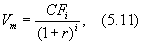
где CFi ¾ ожидаемый денежный поток в i-м периоде (обычно год), д. е.;
r ¾ требуемая инвестором ставка дохода, коэфф.;
i ¾ номер периода.
Акция имеет номинальную, балансовую, ликвидационную, рыночную цены.
Номинальная цена¾это цена, напечатанная на бланке акции или установленная при ее выпуске.
Возникает вопрос: насколько номинальная цена пригодна для оценки реальной стоимости акции? Номинал возникает в момент рождения акционерного общества и показывает, какая часть стоимости уставного капитала приходилась на одну акцию на момент его формирования. Уже на второй день жизни общества его акционерный капитал будет отличаться от размера уставного, зафиксированного в учредительных документах. Номинальная цена пригодна для оценки реальной стоимости акции примерно так, как улыбка американского президента, изображенного на долларовой банкноте, для оценки достоинства этой банкноты.
Вы можете поместить на бланке акции портрет Джоконды с ее загадочной улыбкой или портрет председателя Совета директоров, если у него симпатичная физиономия, или (что практически равнозначно) напечатать номинальную цену. По этой причине в некоторых странах, в частности, в США, акции выпускаются без указания номинала. В этом случае, чтобы провести ценные бумаги по учету, используют так называемую объявленную стоимость, которая отражается (объявляется) в проспекте эмиссии.
Балансовая цена¾это стоимость чистых активов акционерного общества, приходящаяся на одну акцию по балансу. Приказ Министерства финансов РФ № 71 и ФКЦБ № 149 от 5 августа 1996 г. определяет порядок оценки стоимости чистых активов акционерных обществ. Однако представляется, что оценивать акцию по ее балансовой цене не вполне корректно. Ведь, приобретая акцию, акционер не покупает долю в имуществе предприятия. Акция не дает права выделения из имущества доли ни в стоимостном, ни в натуральном выражении. В этом заключается ее коренное отличие от пая.
Балансовая цена (в отличие от номинальной и объявленной) изменяется от периода к периоду. Но и она тоже недостаточна для оценки реальной стоимости акции. Например, на балансе имущество может числиться в ценах приобретения, а текущая его цена, особенно в условиях инфляции, может быть существенно выше. Противоположная ситуация: имущество морально устарело и не находит сбыта, хотя балансовая цена его достаточно высока. В этом случае на арену действия выходит ликвидационная цена.
Ликвидационная цена¾стоимость реализуемого имущества акционерного общества в фактических ценах, приходящаяся на одну акцию. Если номинал характеризует цену акции в момент рождения предприятия, то ликвидационная ¾ в момент его смерти. Обе эти цены мимолетны и применяются в особых ситуациях. Например, если решается вопрос о реорганизации или ликвидации АО. Естественно, что обе эти цены не могут использоваться при оценке акций нормально действующего общества.
Рыночная (курсовая) цена¾это цена, по которой акция продается и покупается на рынке.
Курс акции ¾рыночная цена, отнесенная к номиналу и выраженная в процентах.
Рассчитать рыночную цену акции значительно сложнее, чем облигации, так как акции ¾ это ценные бумаги с изменяющимся доходом, величина которого зависит от многих факторов, в отличие от облигаций, где доход либо фиксирован, либо изменяется с определенной закономерностью. Для расчета курсов акций используются различные модели. Наиболее известной из них является модель М. Гордона, имеющая ряд модификаций.
1. Темп прироста дивидендов (g) равен нулю, т. е. g = 0. В этом случае текущая рыночная цена акции (P0) определяется по формуле:
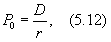
где P0 ¾ текущая цена акции, д. е.;
D ¾ текущий дивиденд, выплачиваемый по акции, д. е.;
r ¾ требуемая инвестором ставка дохода, коэфф.
2. Темп прироста дивидендов постоянен, т. е. g = const. В этом случае P0рассчитывается по формуле:
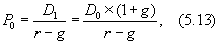
где D0, D1 ¾ величина дивиденда, соответственно, последнего выплаченного и ближайшего прогнозируемого, д. е.
Пример.
Акция приобретена за 500 д. е.; прогнозируемый дивиденд следующего года составит 20 д. е. Ожидается, что в последующие годы этот дивиденд будет возрастать с темпом 12%. Какова приемлемая норма прибыли, использованная инвестором при принятии решения о покупке акции?
Из формулы (5.13) выразим r:
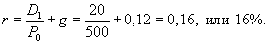
3. Темп прироста дивиденда меняется, т. е. g ¹ const. В этом случае Po рассчитывается по формуле:
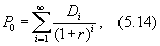
где Di ¾ величина дивидендов в i-м периоде, д. е.;
i ¾ номер периода начисления дивидендов.
4. Динамика темпа прироста дивидендов неравномерна, т. е. в первые годы g ¹ const, а затем величина дивидендов приобретает среднюю динамику (g = p):
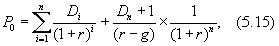
где n ¾ общее количество лет анализа;
i ¾ число лет с изменяющимся темпом прироста дивидендов.
Пример.
В течение последующих четырех лет компания планирует выплачивать дивиденды соответственно 1,5; 2; 2,2; 2,6 долл. на акцию. Ожидается, что в дальнейшем дивиденд будет увеличиваться равномерно с темпом 4% в год. Рассчитать теоретическую стоимость акции, если рыночная норма прибыли 12%:
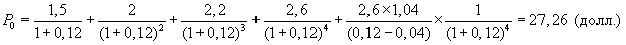
На практике стоимость акций компании часто определяется на основе размеров прибыли, а не дивидендов. Стратегический инвестор видит в денежных потоках, генерируемых компанией, основу будущих дивидендных выплат, поэтому он обосновывает свой выбор направлений вложения денежных средств путем расчета и анализа ценовых мультипликаторов.
Ценовый мультипликатор ¾ это коэффициент, показывающий соотношение между рыночной ценой акции и финансовой базой. Финансовая база оценочного мультипликатора является измерителем, отражающим финансовые результаты деятельности организации, к которым можно отнести не только прибыль, но и денежный поток, дивидендные выплаты, выручку от реализации и др.
В оценочной практике используется два типа мультипликаторов: интервальные и моментные. К первому типу можно отнести мультипликаторы: цена/прибыль (P/E); цена/денежный поток (P/CF); цена/дивиденд (P/D); цена/выручка от реализации (P/S). Ко второму типу относятся: цена/балансовая стоимость; цена/чистая стоимость активов.
Наиболее часто используются показатели P/E и P/CF. В качестве финансовой базы для первого из них может использоваться любой показатель прибыли: чистая прибыль; прибыль до налогообложения; прибыль до уплаты процентов и налогов. Рассчитанный показатель для оцениваемой компании сравнивается с соответствующим показателем компании-аналога или со средним по рынку акций в целом. При сравнении необходимое требование: чтобы финансовая база была идентичной.
В качестве базы для расчета мультипликатора P/E можно использовать не только сумму прибыли, полученную в последний год перед датой оценки, но и среднегодовую сумму прибыли за последние пять лет. Цена акции берется на последнюю дату, предшествующую дате оценки, либо она представляет среднюю величину между максимальной и минимальной величиной цены за последний месяц. Значение данного мультипликатора может служить мерой риска для инвесторов и в то же время сроком окупаемости своих затрат, осуществленных при покупке данной акции. Низкое значение данного коэффициента указывает на высокий уровень риска (либо слабые перспективы для роста прибылей). Высокое значение этого коэффициента означает низкий уровень риска, хорошие перспективы роста прибылей и дивидендов, но в то же время достаточно длительный срок окупаемости затрат.
Однако если этот коэффициент для данной компании ниже, чем в среднем для данного сектора экономики, то это означает потенциальный рост цен акций данной компании, если только есть возможность и предпосылки для роста прибылей. С другой стороны, низкое значение этого коэффициента может означать, что компания испытывает затруднения, а перспективы роста неопределенны.
Среднее значение показателя цена/прибыль для большинства развитых рынков находится в диапазоне 12-18. Обычно он повышается в период биржевого бума. Продолжавшийся несколько лет подъем на большинстве развитых рынков привел к повышению коэффициента цена/прибыль до 24-34 и снижению текущей доходности до 1-2%. Среди развитых стран в 80-90-е годы этот показатель характеризовался самыми высокими значениями в Японии. В конце 80-х годов он доходил здесь до 60, а у некоторых компаний до 200. В России в период пика этот показатель достигал в августе-сентябре 1997 г. 12-13, а к сентябрю-октябрю 1998 г. снизился до рекордно низких величин ¾ 1,7 и 2,6.
Мультипликатор P/E можно использовать для определения стоимости акций лишь в том случае, если рост прибылей в расчете на акцию стабилен. Если этот рост колеблется из года в год, то стоимость акции нельзя определить на основе значения прибыли на акцию лишь за последний год. При выпуске акций молодых перспективных компаний фиксируется астрономическое значение мультипликатора P/E. Так, для акций пионера в генной инженерии американской компании «Дженентекс» P/E вскоре после выпуска составлял 3500 (а в среднем для представленных на биржекорпораций этот показатель равнялся в то время 9).
Наиболее распространенной ситуацией применения мультипликатора P/CF является убыточность либо незначительная величина прибыли, а также несоответствие фактического полезного срока службы основных фондов организации периоду амортизации, принятому в финансовом учете. Это возможно в случае, когда стоимость активов будет незначительной, хотя прослужат они довольно долго.
Мультипликатор P/D может рассчитываться как на базе фактически выплаченных, так и на основе потенциальных дивидендов. Под потенциальными дивидендами понимаются типичные дивидендные выплаты по группе сходных организаций, исчисленные в процентах к чистой прибыли. Данный мультипликатор целесообразно использовать, если дивиденды выплачиваются достаточно стабильно либо способность компании платить дивиденды может быть обоснованно спрогнозирована.
Пример.
Используя нижеперечисленную информацию, вычислите мультипликаторы P/E, P/CF, P/S.
Фирма «Салют» имеет в обращении 25 000 акций. Рыночная цена одной акции ¾ 20 д. е.
Отчет о прибылях и убытках (выписка):
1. Выручка от реализации 500 000 д. е.
2. Затраты 400 000 д. е.,
в том числе амортизация 120 000 д. е.
3. Сумма уплаченных процентов 30 000 д. е.
4. Ставка налога на прибыль 30%.
Чистая прибыль компании составила:
E = (500 000 - 400 000 - 30 000) ´ 0,7 = 49 000 (д. е.);
E (на одну акцию) = 49 000 д. е. : 25 000 = 1,96 д. е.
Денежный поток составил:
CF = 49 000 + 120 000 = 169 000 (д. е.);
CF (на одну акцию) = 169 000 д. е. : 25 000 = 6,76 д. е.;
S (на одну акцию) = 500 000 д. е. : 25 000 = 20 д. е.
Рыночная цена всех акций, находящихся в обращении:
20 д. е. ´ 25 000 = 500 000 д. е.
Рассчитаем мультипликаторы:
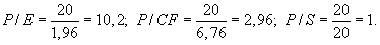
Для большинства российских акционерных обществ оценить рыночную стоимость акций достаточно сложно хотя бы потому, что их акции не обращаются в организованных торговых системах. Статья 77 ФЗ «Об акционерных обществах» гласит: «В случаях, когда в соответствии с настоящим Федеральным законом цена (денежная оценка) имущества, а также цена размещения или цена выкупа эмиссионных ценных бумаг общества определяются решением Совета директоров (наблюдательного совета) общества, они должны определяться исходя из их рыночной стоимости.
Если лицо, заинтересованное в совершении одной или нескольких сделок, при которых цена (денежная оценка) имущества определяется Советом директоров (наблюдательным советом) общества, является членом Совета директоров (наблюдательного совета) общества, цена (денежная оценка) имущества определяется решением членов Совета директоров (наблюдательного совета) общества, не заинтересованных в совершении сделки. В обществе с числом акционеров 1000 и более цена (денежная оценка) имущества определяется независимыми директорами, не заинтересованными в совершении сделки.
Привлечение независимого оценщика является обязательным для определения цены выкупа обществом у акционеров принадлежащих им акций…, а также в иных случаях, предусмотренных настоящим Федеральным законом.
В случае определения цены размещения ценных бумаг, цена покупки или цена спроса и цена предложения которых регулярно опубликовываются в печати, привлечение независимого оценщика необязательно, а для определения рыночной стоимости таких ценных бумаг должна быть принята во внимание эта цена покупки или цена спроса и цена предложения...
В случае, если владельцем более 2% голосующих акций общества являются государство и (или) муниципальное образование, обязательно привлечение государственного финансового контрольного органа».
Порядок оценки рыночной стоимости имущества акционерного общества в соответствии с ФЗ «Об акционерных обществах» от 26 декабря 1995 г. № 208-ФЗ (в ред. от 7 августа 2001 г. № 120-ФЗ) представлен на рис. 5.1.
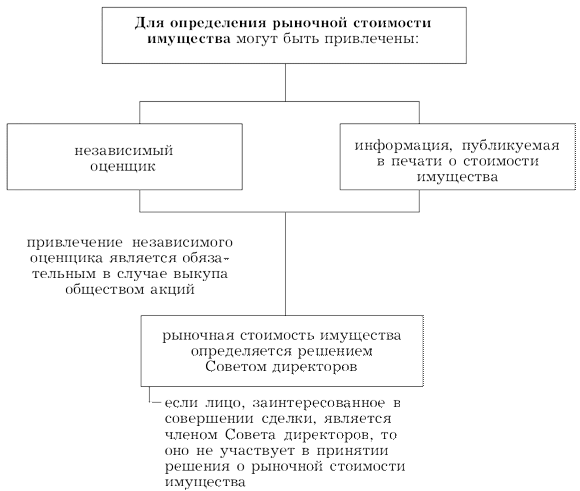
Рис. 5.1. Определение рыночной стоимости имущества
акционерного общества
Перейдем к рассмотрению видов цен на облигации. Облигация имеет нарицательную (номинальную), выкупную, рыночную цены.
Номинальная цена напечатана на бланке облигации и обозначает сумму, которая берется взаймы и подлежит возврату по истечении срока облигационного займа. В отличие от номинальной цены акции номинальная цена облигации представляет существенный интерес для инвестора, так как она служит базой для начисления процентов.
Выкупная цена(которая может совпадать, а может и не совпадать с номинальной, что определяется условиями займа) ¾ это цена, по которой эмитент выкупает облигацию у инвестора по истечении срока займа. В соответствии с российским законодательством выкупная цена должна совпадать с номинальной.
Рыночная цена¾это цена, по которой облигация продается и покупается на рынке.
Курс облигации¾ это значение рыночной цены, выраженное в процентах к ее номиналу.
Купонный доход по облигациям выплачивается периодически. При продаже облигаций в дни, не совпадающие с днями выплаты текущего дохода, покупатель и продавец должны разделить между собой сумму процентов. С этой целью покупатель уплачивает продавцу помимо рыночной цены облигации проценты, причитающиеся за период, прошедший с момента их последней выплаты, ¾ так называемый накопленный купонный доход. Сам же покупатель при наступлении следующей даты выплаты купонного дохода получит его полностью за весь купонный период. Таким образом, сумма процентов распределяется между различными владельцами облигации. Накопленный купонный доход (А) можно рассчитать по формуле:
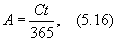
где С ¾ годовая купонная ставка в процентах к номиналу или в д. е.;
t ¾ количество дней со дня выплаты последнего купонного дохода до дня продажи.
Рыночная цена с учетом накопленного купонного дохода называется «грязной» ценой.
Пример.
Определите, по какому курсу должна быть совершена сделка купли-продажи облигации на предъявителя при условии, что годовой купон равен 10%. Сделка заключается за 18 дней до выплаты дохода. Расчетный год ¾ 360 дней. Прочие ценообразующие факторы и налогообложение не учитывать.
Рассчитаем накопленный купонный доход по формуле:
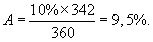
Поскольку прочие ценообразующие факторы не учитываются, то можно предположить, что рыночная цена облигации совпадает с номинальной. Поэтому рыночная цена с учетом НКД («грязная» цена) будет равна:
100% + 9,5% = 109,5%.
Облигация с нулевым купоном (с дисконтом)¾ это облигация, по которой текущий доход не выплачивается; облигация продается по цене ниже номинала, а погашается по номиналу. Текущая стоимость такой облигации определяется по формуле:
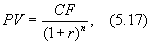
где PV ¾ текущая стоимость облигации, д. е.;
CF ¾ сумма, выплачиваемая при погашении облигации, д. е.;
r ¾ требуемая инвестором ставка дохода в долях единицы;
n ¾ число лет, по истечении которых произойдет погашение облигации.
Пример.
Облигация с нулевым купоном нарицательной стоимостью 100 д. е. сроком погашения два года продается за 64 д. е. Определите целесообразность приобретения этой облигации, если имеется возможность альтернативного вложения капитала по ставке 15% годовых.
При ответе на поставленный вопрос можно использовать несколько способов решения задачи.
Первый способ. Рассчитаем текущую стоимость облигации, используя формулу (5.17):
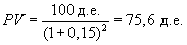
Поскольку текущая стоимость выше фактической, то этот факт говорит о том, что данная ценная бумага недооценена рынком. Следовательно, инвестор может принимать положительное решение по поводу покупки данной облигации.
Второй способ. Рассчитаем наращенную (будущую) стоимость облигации:
CF = 64 д. е. ´ (1 + 0,15)2 = 84,61 д. е.
Таким образом, если бы инвестор вложил 64 д. е. в альтернативную инвестицию с рыночной ставкой дохода, то через два года он получил бы 84,61 д. е. Вкладывая деньги в облигацию, он получит сумму, равную номиналу (100 д. е.). Вывод совпадает с предыдущим результатом.
Третий способ. Попытаемся ответить на вопрос: какова ставка дохода по вложениям в данную облигацию? Для этого преобразуем формулу (5.17) и подставим в нее известные значения:
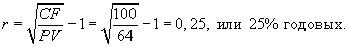
Следовательно, ставка дохода по данной облигации значительно выше среднерыночной, что может служить обоснованием для принятия решения о вложении денежных средств.
Купонной называется облигация, по которой текущий (купонный) доход выплачивается с определенной периодичностью (по кварталам, полугодиям, раз в год). Текущая стоимость купонной облигации рассчитывается по формуле:
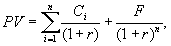(5.18)
где PV ¾ текущая стоимость облигации, д. е.;
Ci ¾ годовой текущий доход в виде процента, выплачиваемый по облигации в i-м периоде, д. е.;
F ¾ сумма, выплачиваемая при погашении, д. е.;
r ¾ требуемая инвестором ставка дохода, коэфф.;
n ¾ число лет, по истечении которых произойдет погашение облигации.
Пример.
По облигации с номиналом 1000 д. е., выпущенной сроком на шесть лет, предусмотрен следующий порядок начисления дохода: первый год ¾ 10%; два последующих года ¾ по 20; оставшиеся три года ¾ по 25. Рыночная норма дохода ¾ 10%. Оцените текущую стоимость облигации:
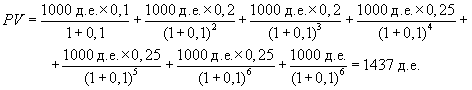
Из приведенных формул и расчетов можно сделать ряд выводов:
1. Если купонная ставка совпадает с рыночной ставкой дохода, то теоретическая оценка облигации совпадает с номинальной ценой. Как правило, в момент выпуска облигации купонная ставка устанавливается на уровне рыночной ставки.
2. В случае, когда рыночная ставка выше, чем купонная ставка, текущая стоимость облигации становится ниже номинала. В этом случае говорят, что облигация продается с дисконтом.
3. В случае, когда рыночная ставка ниже, чем купонная ставка, текущая стоимость облигации становится выше номинала. В этом случае говорят, что облигация продается с премией (ажио).
4. Если облигация приобретена по номиналу, то ее текущая доходность и доходность до погашения идентичны купонной.
5. Если облигация приобретена по цене ниже номинала, то ее текущая доходность и доходность до погашения выше купонной.
6. Если облигация приобретена по цене выше номинала (с премией), то ее текущая доходность и доходность до погашения ниже купонной.
Пример.
Выберите правильные, на ваш взгляд, варианты ответов в каждой из трех предложенных ситуаций.
Облигация со сроком обращения три года продается по курсу 105% и имеет текущую доходность 18% годовых. Какой может быть ее доходность до погашения (без учета налогообложения):
а) 10% годовых; б) 18% годовых; в) 21% годовых?
Облигация со сроком обращения пять лет и купонной ставкой 20% продается по курсу 85%. Какой уровень доходности до погашения не может иметь эта облигация (без учета налогообложения):
а) 15% годовых; б) 20% годовых; в) 30% годовых?
Купонная доходность облигации равна ее доходности до погашения. По какой цене продается облигация:
а) меньше номинала; б) равной номиналу; в) больше номинала?
При осуществлении фундаментального анализа возникает ряд трудностей:
¨ информация, используемая при фундаментальном анализе, может оказаться недостаточно точной; «творческий» бухгалтерский учет, как правило, скрывает неблагоприятные показатели деятельности организации;
¨ организации и отрасли в значительной мере подвержены влиянию неопределенности, которая изменяет основные переменные анализа, и таким образом делают его малопригодным;
¨ логично предположить, что при большом количестве рационально действующих аналитиков все результаты фундаментального анализа будут отражены уже в текущей цене.
Технический анализ
Отличительной особенностью фондового рынка является то, что он более всего отвечает критерию совершенной конкуренции: централизованное ведение торгов, однородная продукция, низкие расходы на проведение сделок, мгновенная связь, достаточно большое количество участников для того, чтобы ни один из них не мог влиять на цены на рынке, а также специальные правила проведения внутренних операций наряду с мерами, обеспечивающими всем участникам рынка доступ к соответствующей информации. Технические методы анализа фондового рынка достаточно разработаны, поскольку профессиональные участники развитых рынков на протяжении значительного периода времени используют технический анализ в качестве метода, помогающего принимать правильные инвестиционные решения. Такое внимание к техническому анализу имеет под собой серьезную основу. Изучение значительных массивов различной информации о рынке дало возможность определить ряд стандартных повторяющихся моделей, характеризующихся определенными признаками.
Отцом технического анализа можно считать Дж. М. Кейнса, поскольку некоторую справедливость его воззрений подтвердила его успешная деятельность на бирже.
Технический анализ представляет собой исследование поведения показателей финансовых рынков с помощью математических моделей разного уровня сложности. Результаты такого исследования используются для прогнозирования изменения цен, объемов, спроса, предложения и т. д. В техническом анализе делается попытка формализовать психологические факторы, играющие существенную роль в формировании тенденций на финансовых рынках. Для успеха биржевой спекулянт должен предугадывать мнение публики, т. е. выбирать инструменты, которые являются перспективными с точки зрения инвесторов. Затем при росте цен на акции вступает в действие механизм «надежды на большего дурака». Другими словами, акции покупают не для того, чтобы держать в течение продолжительного времени, а потому что верят, что найдутся инвесторы, готовые предложить больше, чем было заплачено. Казалось бы, многочисленные «мыльные пузыри» подтверждают значимость психологических факторов, но ценность методик прогноза заключается не в выявлении факторов, а в нахождении способа применения их на практике.
В техническом анализе используются количественные данные и исторические сведения о ценах. Он базируется на трех исходных положениях. Во-первых, изменение цен и других показателей на сбалансированных финансовых рынках обладает инерцией, поэтому имеется возможность отслеживать тенденции. Во-вторых, существовавшие в прошлом модели изменения цен повторяются, и, в-третьих, вся информация, необходимая для принятия решения по инвестиции, содержится в рыночной цене.
Действительно, изучение графиков изменения цен показало, что в большом числе случаев «психологическое поведение» цен повторяется. Во многом это связано с тем, что сдвиги спроса и предложения предсказуемы в рамках определенных моделей и что быстрые изменения в ценах происходят тогда, когда происходят быстрые сдвиги в спросе и предложении. Это также связано с принципом «и я тоже», когда инвесторы боятся отстать в случае возникновения таких сдвигов. Технический анализ акцентирует внимание на состояниях рынка, определяемых, как «рынок, перенасыщенный покупкой», и «рынок, перенасыщенный продажей».
В процессе проведения технического анализа используются три аксиомы.
Дата добавления: 2016-08-08; просмотров: 858;