Анализ резисторного каскада в области нижних частот.

В области низких частот проводимость 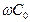незначительна, и ею можно пренебречь. Сопротивление Х_со=1/jωC0 велико. Следовательно, эта цепь шунтирующего влияния не оказывает. Однако в области низких частот необходимо учитывать влияние реактивного сопротивления емкости С1, так как сопротивление Х_С1= 1/jωC1 возрастает, на нем происходит падение нап­ряжения, вследствие чего уменьшается 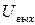и коэффициент усиления. Поэтому эквивалентная схема в области нижних частот примет вид, изображенный на рис.6.6,а.

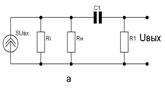
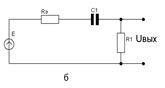
Рис.6.6.Эквивалентные схемы усилителя в области НЧ: а – с генератором тока; б – с генератором ЭДС.

Для упрощения дальнейших выкладок преобразуем эквивалентную схему с гене­ратором тока в эквивалентную схему с генератором ЭДС (рис.6.6,б), где R_э=R_iR_н/(R_i+R_н),E=SU_вхR_э

Ток и напряжение в выходной цепи:

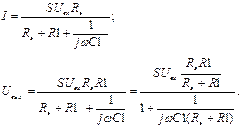(6.13)

Комплексный коэффициент усиления в области низких частот соответственно определяется:

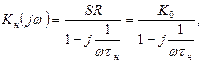(6.14)

где 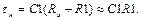, т.к. R_э<< R1;

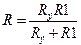
Определим модуль комплексного коэффициента усиления в области низких частот

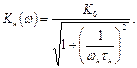(6.15)

В соответствии (6.15) построим график АЧХ на нижних частотах, рис.6.7.

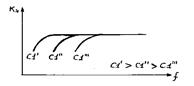
Рис.6.7. АЧХ в области НЧ при различных значениях разделительной емкости

Анализируя выражение (6.15), приходим к выводу, что частот­ная характеристика в области низких частот определяется в основ­ном значением разделительной емкости С1.

Для нахождения нижней граничной частоты приравниваем выра­жение (6.15) к значению :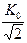

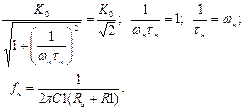(6.16)

Для расширения полосы пропускания усилителя в сторону низ­ких частот необходимо увеличивать постоянную времени 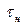. Однако это ограничивается несколькими факторами. Практически постоянная времени 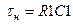должна быть не больше 0,01¸0,1 сек., что не позволяет усиливать колебания с частотами ни­же нескольких герц.

Рассмотрим фазовый сдвиг 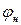, создаваемый усилителем в области низких частот. Тангенс фазового сдвига 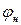равен отношению мнимой части к его вещественной части :

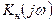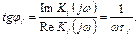(6.17)

По мере понижения частоты фазовый сдвиг 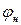(сверх 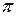) асимп­тотически стремится к 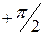, рис.6.8.

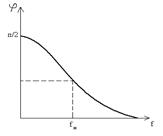
Рис.6.8. ФЧХ в области НЧ.

При 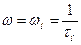имеем

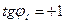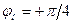, (6.18)

т.е. нижней пороговой частоте соответствует фазовый сдвиг (сверх 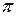), равный +45°. Очевидно, при этой частоте модуль емкостного сопротивления 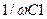равен активному сопротивлению .

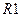Выражая 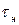через нижнюю пороговую частоту, можно записать уравнение фазочастотной характеристики для области низких частот в виде:

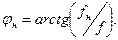(6.19)

Зависимость фазового сдвига 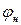от частоты, представлена на рис.6.8.

Коэффициент частотных искажений на нижней граничной частоте

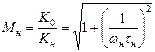. (6.20)

Решая выражение 6.20 относительно 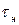, получим расчетную формулу:

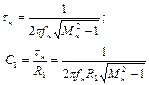. (6.21)

Следовательно, разделительная емкость С1 рассчитывается из необходимости удовлетворения основных технических требований к усилителю в области низких частот.

Лекция №7