Геометрический ряд частот вращения

Ряд частот вращения, содержащий z значений частот, может быть построен следующим образом:

…;

…;

.

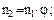
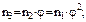
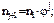
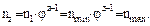Очевидно, 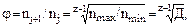где .

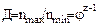Прологарифмируем последнее выражение:

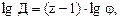откуда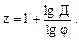

В выражениях – знаменатель геометрической прогрессии, называемый знаменателемряда.

Очевидно: 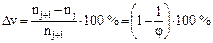и для конкретного значения φ ∆v=сonst, т.е. в геометрическом ряде обеспечивается постоянный перепад скоростей. Лучевая диаграмма для него показана на рис. У.8.

Запишем в качестве примера ряд, в котором n1=10, z=8, =2 и сравним первую по порядку половину чисел со второй: 10 – 20 – 40 – 80 – – 160 – 320 – 640 – 1280; в этом ряду: 10/160= 20/320= 40/640= 80/1280 =1/16. Как видно, геометрический ряд позволяет получать кратные частоты вращения. Это даёт возможность строить сложные коробки скоростей из нескольких элементарных двухваловых групповых передач, размещаемых последовательно. Впервые целесообразность применения геометрического ряда для приводов станков была обоснована русским академиком А.В. Гадолиным в 1876 году.

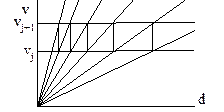Рис. У.8. Лучевая диаграмма для геометрического ряда частот вращения

Геометрические ряды применяются также в общей стандартизации машиностроения.