Принцип суперпозиции электрических

Полей

Если электрическое поле создается заря-дами Q₁, Q₂, … , Q_n, то на пробный заряд Q₀действует сила Fравная векторной сумме сил F_i , приложенных к нему со стороны каждого из зарядов Q_i:

.

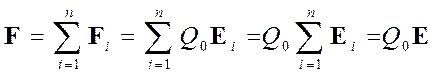Вектор напряженности электрического поля системы зарядов равен геометрической сумме напряженностей полей, создаваемых каждым из заря­дов в отдельности:

.

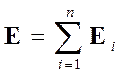Эта принцип суперпозиции (наложения) электростатических полей.

Принцип гласит: напряженность Е результирующего поля, создаваемого систе-мой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.

Принцип суперпозиции позволяет рассчи-тать электростатические поля любой си­стемы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов.

Поле диполя. Принцип суперпозиции применим для расчета электростатического поля элект­рического диполя.

Электрический диполь - система двух равных по модулю разноименных точечных зарядов (+Q, -Q),расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля. Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними, называется плечом диполя l. Вектор

,

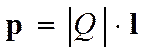совпадающий по направлению с плечом ди-поля и равный произведению заряда 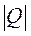на плечо l, называется электрическим момен-том диполяили дипольным моментом (рис.11.7).

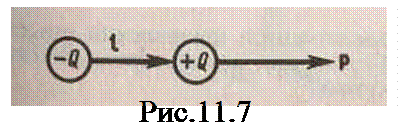
Согласно принципу суперпозиции полей, напряженность Е поля диполя в произ­вольной точке

Е=Е₊+Е_- ,

где Е₊ и Е_- - напряженности полей, создавае-мых соответственно положительным и отри-цательным зарядами.

Воспользовавшись этой формулой, рассчитаем напряжен­ность поля в произвольной точке на продолжении оси диполя и на перпендикуляре к середине его оси.

1. Напряженность поля на продолжении оси диполя в точке А (рис.11.7).

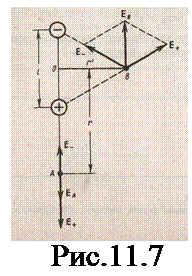Как видно из рисунка, напряженность поля диполя в точке А направлена по оси диполя и по модулю равна

Е_А=Е₊-Е_- .

Обозначив расстояние от точки А до середины оси диполя через r, на основании формулы (11.2) для вакуума можно записать

.

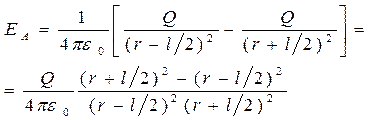Согласно определению диполя, l/2<<r, поэтому

.

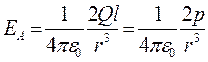2. Напряженность поля на перпендикуляре, восставленном к оси из его середины, в точке В(рис.11.7). Точка В равноудалена от зарядов, поэтому

,

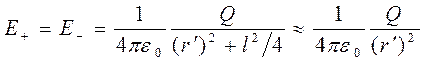где r' — расстояние от точки В до середины плеча диполя. Из подобия равнобедренных треугольников, опирающихся на плечо диполя и вектор Е_В получим

,

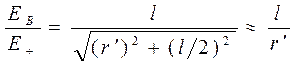откуда .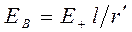

Подставив в последнее выражение значение Е₊, получим

.

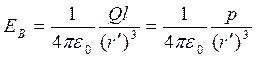Вектор Е_В имеет направление, противоположное вектору электрического момента диполя (вектор р направлен от отрицательного заряда к положительному).