Лекция: Основы принятия решений и ситуационного моделирования

Рассматриваются основные понятия теории принятия решений и ситуационного моделирования систем, примеры.

Цель лекции:содержательное введение в основы принятия решений и ситуационное моделирование систем.

Принятие решения и целеполагающая ресурсоориентированная деятельность человека в социальной, экономической, политической, идеологической, военной сферах тесно связаны. В них крайне нежелательны ошибки, которые могут привести к пагубным последствиям. Но из-за ограниченных информационных возможностей человека ошибки всегда возможны. Поэтому есть настоятельная необходимость применения научного подхода к обоснованию и принятию решений.

Принятие решений, наряду с прогнозированием, планированием, ситуационным анализом обстановки, исполнением решений, контролем и учетом является функцией управления. Все функции управления направлены так или иначе на формирование или реализацию решений, и любую функцию управления технологически можно представить в виде последовательности каких-либо связанных общей целью решений.

При прогнозировании и планировании принимаются решения, связанные с выбором методов и средств, организацией работы, оценкой достоверности информации, выбором наиболее достоверного варианта прогноза и наилучшего варианта плана. Таким образом, функция принятия решений является с методологической и технологической точек зрения более общей, чем другие функции управления. Для лица, принимающего решение (ЛПР), принятие решений является основной задачей, которую он обязан исполнять в процессе управления. Поэтому знание методов, технологий и средств решений этой задачи является необходимым элементом квалификации руководителя, базой для дальнейшего управления.

Конечным результатом любой задачи принятия решений становится решение, конструктивное предписание к действию. Решение является одним из видов мыслительной деятельности и имеет следующие признаки: имеется выбор из множества возможностей; выбор ориентирован на сознательное достижение целей; выбор основан на сформировавшейся установке к действию. Основной характеристикой решения является его эффективность, т.е. степень, темп достижения целей и затраты ресурсов для принятия и реализации решения. Решение тем эффективнее, чем больше степень достижения целей и меньше стоимость затрат.

Принятие решения - это выбор одного из множества рассматриваемых допустимых вариантов. Обычно их число конечно, а каждый вариант выбора определяет некоторый результат (экономический эффект, прибыль, выигрыш, полезность, надежность и т.д.), допускающий количественную оценку. Такой результат обычно называется полезностью решения. Таким образом, ищется вариант с наибольшим значением полезности решения. Возможен и подход с минимизацией противоположной оценки, например, отрицательной величины полезности. Часто на практике встречается ситуация, когда каждому варианту решения соответствует единственный результат (детерминированность выбора решения), хотя возможны и другие случаи, например, когда каждому варианту i и условию j, характеризующему полезность, соответствует результат решения x_ij. Таким образом, можно говорить о матрице решений ||x_ij||, i=1,2,:m; j=1,2,:,m. Чтобы оценить решение, необходимо уметь оценивать все его последствия. Существуют различные подходы для такой оценки. Например, если решения альтернативные, то можно последствия каждого из них характеризовать суммой его наибольшего и наименьшего результатов, максимумом из возможных таких сумм, максимумом из максимумов по всем вариантам (оптимистическая позиция выбора), максимумом из среднего арифметического (нейтральная позиция выбора), максимумом из минимума (пессимистическая позиция) и другие.

Классические модели принятия решений, как правило, являются оптимизационными, ставящими цель максимизировать выгоду и на основе этих моделей получить практическую прибыль. Так как теоретиков больше интересует первая сторона, а практиков - вторая, то при разработке и использовании таких моделей необходимо их тесное сотрудничество. Практические рекомендации (решения) могут быть получены, если при построении модели принятия решений придать большее значение учету существенных структурных элементов моделируемой системы, т.е. разработке имитационной модели принятия решений, с привлечением экспериментальных, полуэкспериментальных и теоретических методов. Кроме классических, оптимизационных процедур принятия решений существуют и ряд базовых неклассических (неоклассических) процедур, технологий принятия решений, некоторые из которых мы рассмотрим.

Классификация задач принятия решений проводится по различным признакам. Наиболее существенными являются: степень определенности информации; использование эксперимента для получения информации; количество лиц, принимающих решения; содержание решений; направленность решений.

На процесс принятия решения часто воздействуют различные случайные (стохастические) параметры, усложняющие процедуру. Недостаток информации об их распределении (сложность их измерения) приводит к необходимости принятия каких-то гипотез как об области их изменения, так и о характере их распределения (о функции распределения вероятностей). Правильность используемых гипотез необходимо проверять с помощью методов оценки статистических гипотез. При отсутствии достаточной информации для такой процедуры приходится привлекать большое число типов распределения. Проблемы принятия решений с недетерминированными параметрами называют проблемами принятия решений в условиях недостатка информации. Чем меньше информации у нас, тем больше может оказаться различие между ожидаемым и действительным результатами принимаемых решений в целом. Мера влияния информации (параметров) на результат решения называется релевантностью. Особо важно в социально-экономической сфере принятие решения при наличии рисков (неплатежей, невозвратов кредитов, ухудшения условий жизни и т.д.).

Формализуемые решения принимаются на основе соответствующих математических методов (алгоритмов). Математическая модель задачи оптимизации формализуемого решения включает следующие элементы:

1. заданную оптимизируемую целевую функцию (критерий управляемости): Ф=F(x₁,x₂,:,x_n), где x_j (j=1,2,:,n) - параметры, учитываемые при принятии решения (отражающие ресурсы принятия решений);
2. условия, отражающие ограниченность ресурсов и действий ЛПР при принятии решений: g_i(x_j)<a_i, k_i (x_j)=b_i; c_j<x_j<d_i, i=1,2,:,m; j=1,2,:, n.

Непременным требованием для решения задачи оптимизации является условие n>m.

В зависимости от критерия эффективности, стратегий и факторов управления выбирается тот или иной метод (алгоритм) оптимизации.

Основными являются следующие классы методов:

1. методы линейного и динамического программирования (принятия решения об оптимальном распределении ресурсов);
2. методы теории массового обслуживания (принятие решения в системе со случайным характером поступления и обслуживания заявок на ресурсы);
3. методы имитационного моделирования (принятие решения путем проигрывания различных ситуаций, анализа откликов системы на различные наборы задаваемых ресурсов);
4. методы теории игр (принятие решений с помощью определения стратегии в тех или иных состязательных задачах);
5. методы теории расписаний (принятие решений с помощью разработки календарных расписаний выполнения работ и использования ресурсов);
6. методы сетевого планирования и управления (принятие решений с помощью оценки и перераспределения ресурсов при выполнении проектов, изображаемых сетевыми графиками);
7. методы многокритериальной (векторной) оптимизации (принятие решений при условии существования многих критериев оптимальности решения)

и другие методы.

Выбор решения - заключительный и наиболее ответственный этап процесса принятия решений. Здесь ЛПР должно осмыслить полученную на этапах постановки задачи и формирования решений информацию и использовать ее для обоснования выбора. В реальных задачах принятия решений к началу этапа выбора решения еще сохраняется большая неопределенность, поэтому сразу осуществить выбор единственного решения из множества допустимых решений практически очень сложно. Поэтому используется принцип последовательного уменьшения неопределенности, который заключается в последовательном трехэтапном (обычно) сужении множества решений. На первом этапе исходное множество альтернативных решений Y сужается (используя ограничения на ресурсы) до множества приемлемых или допустимых решений Y₁ Y. На втором этапе множество допустимых решений Y₁ сужается (учитывая критерий оптимальности) до множества эффективных решений Y₂ Y₁. На третьем этапе осуществляется выбор (на основе критерия выбора и дополнительной информации, в том числе и экспертной) единственного решения Y* Y₂.

Система принятия решений - совокупность организационных, методических, программно-технических, информационно-логических и технологических обеспечений принятия решений для достижения поставленных целей.

Общая процедура принятия решений может состоять из следующих этапов:

• анализ проблемы и среды (цели принятия решения, их приоритеты, глубина и ограничения рассмотрения, элементы, связи, ресурсы среды, критерии оценки);
• постановка задачи (определение спецификаций задачи, альтернатив и критериев выбора решения);
• выбор (адаптация, разработка) метода решения задачи;
• выбор (адаптация, разработка) метода оценки решения;
• решение задачи (математическая и компьютерная обработка данных, имитационные и экспертные оценки, уточнение и модификация, если это необходимо);
• анализ и интерпретация результатов.

Задачи принятия решений могут быть поставлены и решены в условиях детерминированных (определенности, формализованности и единственности целевой функции, ее количественной оцениваемости), риска (возможные решения, исходы распределены вероятностно) и недетерминированных (неопределенности, неточности, плохой формализуемости информации).

В моделях принятия решений используются различные процедуры. В частности, наиболее просты и эффективны следующие:

• методы математического программирования;
• методы кривых безразличия;
• многокритериального выбора альтернатив на основе четкого или же нечеткого отношения предпочтения;
• последовательной оценки и последующего исключения вариантов;
• многомерного ранжирования (шкалирования) объектов и другие.

При выборе pационального pешения необходимо принимать во внимание внешнюю сpеду и побочные явления, динамическую изменчивость критериев оценок решения, необходимость ранжирования аспектов и приоритетов решения, их неполноту и разнородность (а иногда и конфликтность).

Продемонстрируем ситуационное моделирование на примере моделирования деятельности банка. Банковская система является одной из подсистем современной экономической системы, наиболее подверженной информатизации. Развитие банковской системы сопровождается постоянным поиском адекватных оптимальных методов и инструментов управления, принятия решений на основе экономико-математического анализа и моделирования деятельности банков. При этом необходимо учитывать тот факт, что финансовые операции имеют еще и стохастические составляющие, усложняющие и без того сложные процессы начисления процентных ставок, взносов и выплат, регулирования и управления, инвестиций и др. Эти процессы сложны не только динамически, но и вычислительно, логически. Кроме того, от таких прогнозов зависят и прогноз, анализ темпов инфляции, структуры активов и пассивов банка, доходности акций, курсов валют, процентная ставка и др.

Ситуационный анализ денежных потоков состоит в основанном - часто на имитационном моделировании - анализе эффективности того или иного набора финансовых операций и процедур (из множества возможных и допустимых) путем сравнения результатов их воздействия на финансовые, денежные потоки с величиной финансовых, денежных активов без учета их воздействия. Следовательно, ситуационный анализ денежных потоков является динамическим процессом, использующим методы оптимизации и критерии оптимальности. При ситуационном анализе некоторых базовых значений величины активов (соответствующих определенным финансовым условиям и обязательствам, например, величине уставного капитала), можно по некоторым критериям оптимальности (целевым функциям оптимизации), выбрать оптимальный набор возможных, допустимых финансовых операций, обеспечивающих, например, наибольшую доходность. Возможно построение целевой функции максимизации с учетом ликвидности. Возможно также получение решения задач, свидетельствующего об отсутствии роста (или малого роста) каких-либо финансовых параметров, например, активов, из которого можно сделать вывод о невозможности проведения оптимизирующих операций (процедур).

Пусть d_t - средний уровень доходности, получаемый в результате проведения некоторых инвестиционных мероприятий, а P_t - процентная ставка на момент времени t=0, 1, 2, ..., T. Тогда рост активов A будет осуществляться по закону

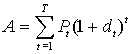
и можно использовать при ситуационном анализе критерий эффективности:

Соотношение между доходностью активов и ценой пассивов коммерческого банка является важнейшим показателем, который отражает эффективность денежно-финансовой политики банка.

Cитуационный анализ соотношения осложняется рядом факторов:

1. структура активов и пассивов могут отражаться ссудами различной длительности, а также различными схемами размещения и привлечения обязательств и ценных бумаг, например, возврат денег может быть осуществлен по схеме ежемесячного отчисления процентов и уплаты кредита в конце либо по схеме единовременного возврата суммы долга и процентов в конце промежутка кредитования;
2. необходимостью учета (прогноза) инфляционного ожидания и "увеличения" или "очистки" тех или иных составляющих активов и пассивов в зависимости от инфляции;
3. различными параметрами и факторами, влияющими на степень риска, затрудненностью оценки величины риска.

Различные структуры и схемы размещения и привлечения финансовых ресурсов определяют и различные динамические модели.

Например, если схема предусматривает возврат долга с процентами одновременно, реальная ставка рублевого кредита d может быть определена по формуле

где z - номинальная ставка рублевого кредита (%), а - инфляция за период кредитования (%).

Для валютного кредита, очищенного от инфляции, с учетом внутренней конвертируемости рубля:

где z - номинальная ставка валютного кредита (%), g - рост курса валюты за период кредитования (%).

Если же договор размещения кредитов предусматривает учет динамики возврата долга (части долга) и уплаты процентов, то реальная ставка может определяться следующей процедурой:

1. определяется динамика срочных выплат (части долга и процентов), гарантирующая полное выполнение обязательств за период кредитования, т.е. обеспечивающая выполнение условий

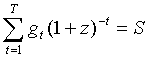
где g_t - ежемесячные (ежеквартальные, ежегодные) выплаты, t - номер месяца (квартала, года), в конце которого происходит выплата, S - размер ссуды, выданной в начале договора кредитования, T - количество дней (месяцев, кварталов, лет) кредитования;

1. задается динамика инфляции, например, дискретная функция a_t=a(t), t=1,2,...,T;
2. определяется реальная ставка d - решение уравнения:

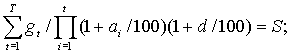
если кредит - валютный, то необходимо дополнить этапы 1-3 этой процедуры следующими этапами:

1. осуществляется прогноз роста курса валюты, т.е. определяется (задается) дискретная функция g_t=g(t), t=1, 2, :, T;
2. реальная ставка определяется из уравнения вида (S - ссуда в валюте):

В долговременных финансово-кредитных операциях проценты либо выплачиваются сразу после их начисления, либо их реинвестируют, применяя сложные проценты. Исходная сумма S (база) увеличивается по принятому (кредитором и дебитором) соглашению, а для простых процентов база постоянная и равна начальной сумме S. Присоединение начисленных процентов к базовой сумме называется капитализацией процентов, t=0,:, T.

Важнейшим показателем при ситуационном анализе и моделировании деятельности и жизнеспособности банка является надежность, банковский или кредитный риск. Надежность банка - не просто вероятность быть надежным банком в данный момент, а вероятность банка сохранять надежностные характеристики и отношения на некотором допустимом промежутке их варьирования и для определенного промежутка времени.

Пусть x=(x₁, x₂, ..., x_n) Ω - вектор, характеризующий надежность банка, а Ω - некоторое множество его допустимых изменений. В качестве меры надежности можно взять условную вероятность p=p(P/Ω), где P - оценка (степень) надежности, P/Ω - оценка при условии изменения x Ω.

Пример. Пусть Ω=Ω(x₁,x₂,x₃) - информационные ресурсы, доступные объекту (субъекту), который производит анализ надежности банка, а x=(x₁,x₂,x₃), где x₁ - активы банка, x₂ - пассивы банка, x₃ - дебиторская задолженность банку. Пусть, например, мы хотим оценить надежность банка, но не имеем о банке информации (или имеем нулевую информацию). Тогда значение p(P/Ω) можно получить, только исходя из двух возможных равновероятных состояний - банк либо надежен, либо не надежен, т.е. p(P/Ω)=0,5. Результат мало информативен и может быть применен к любому банку при любых условиях Ω. Пусть теперь известно, что существует лишь 30 % надежных банков, т.е. мы при оценке надежности банка используем эту информацию. В этом случае можно оценить надежность банка как 0 p(P/Ω) 0,3. В то же время, как и для предыдущего случая, такая оценка надежности будет малоинформативной, так как здесь мы имеем, как и в первом случае, два возможных состояния (p 0,3 и p>0,3) и по формуле Шеннона количество информации в том и в другом случае равно

Чем более точной информацией о банке владеет вкладчик (дебитор), тем проще ему можно принимать верные решения, т.е. тем чаще и ближе будут оценки вероятности (надежности) p к p=0 и p=1. Чем меньше информации, тем сложнее принять однозначное решение, тем чаще и ближе будет оценка вероятности к p=0,5 ("пятьдесят на пятьдесят").

Величину p(P/Ω) принято называть апостериорной вероятностью (a posteriori - после опыта). Под опытом здесь подразумевается процесс получения информации Ω, следовательно, p(P/Ω) - вероятность быть надежным банком с учетом полученной в результате опыта информации.

При определении надежности (например, экспертами) могут допускаться ошибки, в том числе и субъективного характера. Это - вероятность "ложной классификации". Пусть p₁ - вероятность отнесения (априори) надежного банка в класс ненадежных, а p₂ - вероятность отнесения (априори) ненадежного банка в класс надежных банков. Если не учитывать гипотез о степени их предпочтения (рейтинг банка), то показатель качества классификации - сумма вероятностей совершения ошибок, т.е. p=p₁+p₂. Можно снабдить их весами (предпочтения) a₁ и a₂, например, если a₁=1, a₂=2, то вероятность p₂ в 2 раза важнее p₁ (иначе говоря, в 2 раза опаснее относить ненадежный банк в группу надежных, чем надежный банк в группу ненадежных). Тогда итоговый показатель является средневзвешенной суммой вероятностей:

где a₁, a₂ 0, q₁, q₂ 0, q₁, q₂- вероятности ошибок, q₁=1-p₁, q₂=1-p₂.

Показатель p называют байесовским риском. Чем больше p, тем хуже произведена классификация, а чем она ближе к нулю, тем классификация ближе к реальной или априорной классификации.

Для ситуационного анализа необходимо иметь адекватные модели потока платежей. Как правило, этот поток - дискретный. Рассмотрим одну из простых подмоделей модели ситуационного анализа, дополняющую выше приведенную процедуру.

Пусть в момент времени t₀=0 имеется капитал x(0) (денежных единиц), а в момент времени t=t₁, t₂, ...,t_n имеются транзакции (приход, расход) y(t_i), i=1,2,...,n. Рассмотрим, как это бывает на практике, одинаковые промежутки времени (год, месяц, день) [t₀;t₁], (t₂;t₃], ..., (t_n-1; t_n], т.е. t_i-t_i-1=const и векторы t=(0, t₁, t₂,...,t_n), x=(x(0), x(t₁), x(t₂), ..., x(t_n)), y=(0, y(t₁), y(t₂), ..., y(t_n)), v=(0, v(t₁), v(t₂), ..., v(t_n)), где v(t_i) - коэффициент дисконта на промежутке времени (0;t_i], т.е. коэффициент относительной скидки или отношения приращения ссуды (капитала) за срок от 0 до t_i к наращенной сумме. Тогда потоки приходов и расходов будут, соответственно, равны

Будем считать доходы кредитора (инвестора) отрицательными величинами (отдает), а поступления - положительными. Тогда z(0)=-x(0) - начальный доход (начальная величина инвестиций), а z(t_i)=y(t_i)-x(t_i) - поступление на его счет, i=1,2,..., n.

Чистая стоимость потока Q=R-P равна:

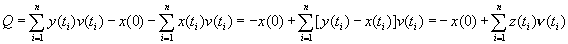
Аналогично, чистое наращенное значение потока на момент времени t_i>0 равно (вводя a(t_j, t_i) - коэффициент наращения на (t_j;t_i],j=1,:,n-1)

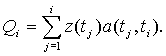
Наращенное значение всех платежей к моменту времени t_n=T равно Q_n.

Одним из эффективных механизмов принятия деловых решений (в проблемах инвестирования, выработки стратегии поведения, развития и т.д.) является использование ИСПР (просто СПР) - информационных систем поддержки решений (Decision Support Systems), сочетающих современные средства аналитической обработки и средства визуализации информации и технологии поддержки деятельности экспертной группы.

Пример. В области организационного управления наибольший интерес имеют так называемые ситуационные (эмерджентные) комнаты (центры), позволяющие быстро "погрузить" ЛПР в рассматриваемую проблемную ситуацию, обстановку, помочь разобраться в проблеме и принять локально-оптимальное (не обязательно глобально-оптимальное) решение. Например, президент США имеет несколько таких комнат. Существуют ситуационные центры Президента РФ, Совета Безопасности, МЧС. Ситуационные комнаты - это специальное место для поддержки построения, проигрывания проблемной ситуации и принятия решений одним человеком или группой людей. Эффект от использования ситуационной комнаты зависит от корректности поставленной проблемы, полноты и достоверности используемых данных, сценария обсуждения, технологий интеллектуальной и компьютерной поддержки (например, использования экспертных систем), временного интервала прогноза и др. Простое использование автоматизированной системы обработки документов, поисковых систем, средств визуализации и мультимедиа - недостаточные условия для функционирования ситуационной комнаты. Основная функция СПР - поддержка умственной, эвристической и творческой деятельности ЛПР. СПР может работать в следующих режимах:

1. проблемный мониторинг и актуализация информации (СМИ, органов власти, объектов управления и пр.) с целью текущего информирования и предупреждения о накапливающихся небольших негативных явлениях;
2. планово-аналитический режим - плановое заслушивание и обсуждение аналитических докладов по проблемной ситуации с целью поддержки и принятия заслушиваемого решения по заранее фиксированному сценарию подачи, демонстрации материала для анализа "вширь" и "вглубь";
3. чрезвычайный режим - оперативный мониторинг информации, принятие и контроль исполнения решений по непредвиденным, чрезвычайным проблемам с целью уменьшения негативных факторов, влияющих на обычное в таких ситуациях совмещение построения сценария, обсуждения и принятия решений.

В базовом варианте, ситуационная комната может включать экран коллективного доступа; компьютер (обычно, ноутбук) с возможностью отображения на экран коллективного доступа; средства доступа к базе данных (знаний), в том числе - с целью сохранения сценария обсуждения, систему подготовки презентаций.

Вопросы для самоконтроля

1. Что такое принятие решения? Что такое полезность решения?
2. Что такое ЛПР, СПР, ИСПР?
3. Как могут классифицироваться задачи принятия решений? Как влияет неопределенность и многокритериальность на такую классификацию и на решение задачи принятия решений?