Частотная модуляция
При частотной модуляции (frequency modulation; FM) мгновенное значение несущей частоты ω(t) связано с модулирующим сигналом e(t) зависимостью (15)
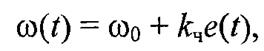
здесь kЧ — размерный коэффициент пропорциональности между частотой и напряжением, рад/(В-с).
Полную фазу ЧМ-сигнала в любой момент времени t определим путем интегрирования мгновенной частоты, выраженной через формулу (15),
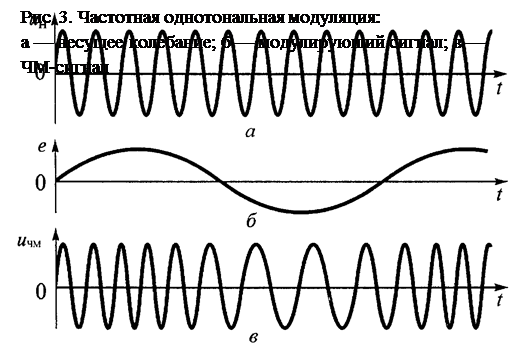 |
(16)
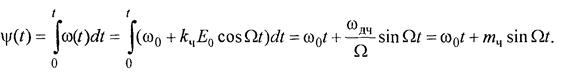
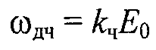
- максимальное отклонение частоты от значения ω0, или девиация частоты (frequency deviation) при частотной модуляции;
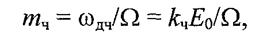 — максимальное отклонение от текущей фазы ω0t или девиация фазы несущего колебания называется индексом частотной модуляции (index of frequency modulation). Данный парамер определяет интенсивность колебаний начальной фазы радиосигнала.
— максимальное отклонение от текущей фазы ω0t или девиация фазы несущего колебания называется индексом частотной модуляции (index of frequency modulation). Данный парамер определяет интенсивность колебаний начальной фазы радиосигнала.
С учетом полученных соотношений (1) и (16) частотно-модулированный сигнал запишется в следующем виде:
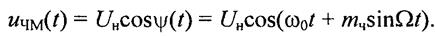
Спектр ЧМ-сигнала при однотональной модуляции.Преобразуем полученное выражение (17)
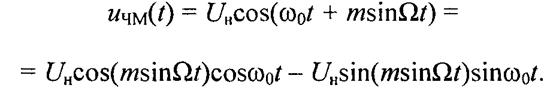
Спектр ЧМ-сигнала при m«1 (такую угловую модуляцию называют узкополосной). В этом случае имеют место приближенные равенства: (18)
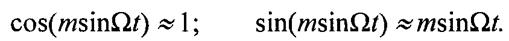
Подставив формулы (18) в выражение (17), после несложных математических преобразований получим (при начальных фазах модулирующего и несущего колебаний θ0 = 0 и φ0 = 0): (19)
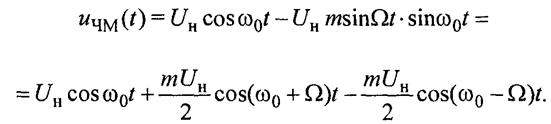
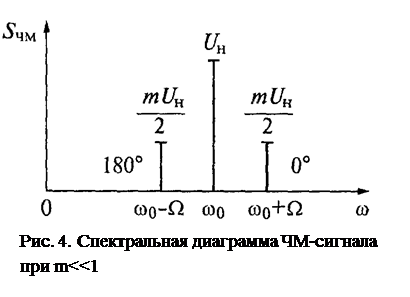
Видим, что по аналитической записи спектр ЧМ-сигнала при однотональной модуляции напоминает спектр АМ- сигнала и также состоит из несущего колебания и двух боковых составляющих с частотами (ω0+ Ω) и (ω0- Ω) причем и амплитуды их рассчитываются аналогично (только вместо коэффициента амплитудной модуляции М в формуле для ЧМ-сигнала фигурирует индекс угловой модуляции m). Но есть и принципиальное отличие, превращающее амплитудную модуляцию в частотную, знак минус перед одной из боковых составляющих.
 |
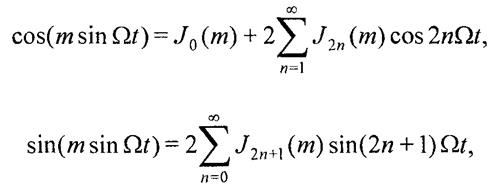 |
Спектр ЧМ-сигнала при m> 1. Из математики известно (20) (21)
где Jn(m) — функция Бесселя 1 -го рода n-го порядка.
В теории функций Бесселя доказывается, что функции с положительными и отрицательными индексами связаны между собой формулой (22)
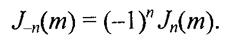
Ряды (20) и (21) подставим в формулу (17), а затем заменим произведение косинусов и синусов полусуммами косинусов соответствующих аргументов. Тогда, с учетом (22), получим следующее выражение для ЧМ-сигнала (23)
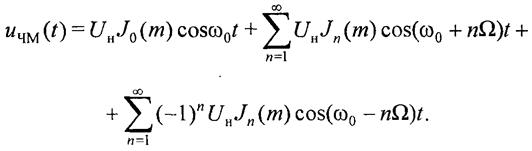
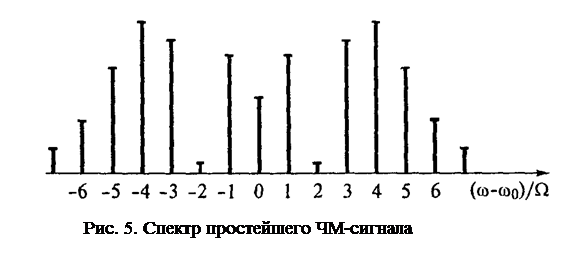
Итак, спектр ЧМ-сигнала с однотональной модуляцией при индексе
модуляции m > 1 состоит из множества высокочастотных гармоник: несущего колебания и бесконечного числа боковых составляющих с частотами ω0+ nΩ. и ω0-nΩ, расположенными попарно и симметрично относительно несущей частоты ω0.
При этом, исходя из (22), можно отметить, что начальные фазы боковых колебаний с частотами ω0+ nΩ. и ω0-nΩ совпадают, если m — четное число, и отличаются на 180°, если m — нечетное. Теоретически спектр ЧМ- сигнала (так же и ФМ-сигнала) бесконечен, однако в реальных случаях он ограничен. Практическая ширина спектра сигналов с угловой модуляцией
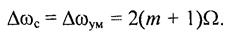
ЧМ- и ФМ-сигналы, применяемые на практике в радиотехнике и связи, имеют индекс модуляции m>> 1, поэтому
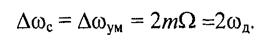
 |
Полоса частот ЧМ-сигнала с однотональной модуляцией равна удвоенной девиации частоты и не зависит от частоты модуляции.
Сравнение помехоустойчивости радиосистем с амплитудной и угловой модуляцией. Следует отметить, что радиосигналы с угловой модуляцией имеют ряд важных преимуществ перед амплитудно-модулированными колебаниями.
1. Поскольку при угловой модуляции амплитуда модулированных колебаний не несет в себе никакой информации и не требуется ее постоянства (в отличие от амплитудной модуляции), то практически любые вредные нелинейные изменения амплитуды радиосигнала в процессе осуществления связи не приводят к заметному искажению передаваемого сообщения.
2. Постоянство амплитуды радиосигнала при угловой модуляции позволяет полностью использовать энергетические возможности генератора несущей частоты, который работает при неизменной средней мощности колебаний.
Дата добавления: 2016-06-02; просмотров: 5667;
