Характеристика САУ. Язык САУ
В ТАУ используются три первичные переменные: вход, выход, ОУ, изображаемые посредством следующей функциональной схемы.

Вход Выход
Рис. 1.
Покажем как пользоваться этими переменными на примере 2-го закона Ньютона. Изменение импульса материальной точки пропорционально приложенной к ней движущей силе F и осуществляется по направлению прямой, вдоль которой эта сила действует. 
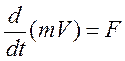 , (1.)
, (1.)
Где: 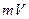 - количество движения (импульс материальной точки).
- количество движения (импульс материальной точки).
После дифференцирования, получим.

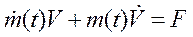 , (2.)
, (2.)
где: 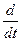 = (.) – обозначение производной, введенное Ньютоном.
= (.) – обозначение производной, введенное Ньютоном.
Если 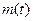 = Const, то уравнение (2.) примет вид
= Const, то уравнение (2.) примет вид
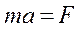 , (3.)
, (3.)
Где: 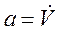 .
.
В соответствии с Рис.1. – ОУ-материальная точка, вход – сила F, выход – ускорение 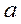 .
.
Причём материальная точка имеет параметр, сосредоточенная в ней масса (m).
Второй закон Ньютона описывает движение материальной точки во времени и в пространстве. Для привязки к пространству необходимо ввести начало отсчёта и систему координат. Поскольку в законе говорится о прямой вдоль которой действует сила, то система координат в неявном виде уже задана. Выберем в качестве направления движения ось Оz в системе отсчёта Oxyz. Тогда z будет обозначать координата положения материальной точки на оси Оz. Введём обозначения 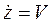 и
и 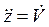 . С учётом этого перепишем (2.) виде:
. С учётом этого перепишем (2.) виде:
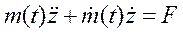 .
.
В ТАУ принято в качестве математических моделей, описываемых дифференциальными уравнениями, использовать приведённые уравнения, в которых коэффициент при старшей производной равен единице. Поэтому в предположении, что 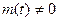 поделим обе части рассматриваемого уравнения на
поделим обе части рассматриваемого уравнения на 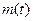 . В результате получим уравнение вынужденного движения объекта управления виде
. В результате получим уравнение вынужденного движения объекта управления виде
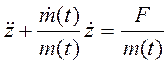 (4.)
(4.)
В уравнении (4.) рассматривается материальная точка и в ней сосредоточена её масса – т.е. рассматривается система с сосредоточенными параметрами. Если же рассматривается движение объекта масса которого распределена в некотором объёме (например ракета), то получим САУ с распределёнными параметрами. Система с сосредоточенными параметрами описывается обыкновенными дифференциальными уравнениями. Их решениями являются функции одной независимой переменной (функции скалярного аргумента), в нашем примере это время. Система с распределёнными параметрами описывается дифференциальными уравнениями в частных производных. Отличительной их особенностью является то, что их решениями являются функции нескольких независимых переменных, т.е. функции векторного аргумента.
В уравнении (4.) время t – непрерывная независимая переменная. Но время может быть и дискретным. С помощью дискретного времени описываются цифровые системы. Термин входное воздействие является собирательным названием терминов: «внешнее воздействие», «управляющее воздействие».
Если коэффициенты уравнений не зависят от времени – САУ стационарная, зависят – САУ нестационарная. Режим работы САУ – описываемый дифференциальными уравнениями называют динамическим, а описываемый алгебраическими уравнениями – статическим.
Если связь между входом и выходом осуществляется через ОУ, то такая САУ называется разомкнутой (Рис.1.). Закон управления физически реализуется посредством регулятора (Рис.2.).
 Вход Выход
Вход Выход
Рис. 2.
Управление, воздействующее на объект независимо от результатов этого воздействия, называется программным управлением или управлением по разомкнутому циклу.

Рис. 3.
Иногда для обозначения этого типа управления используется термин управление по возмущению. А система САУ называется разомкнутой.
Управление, воздействующее на объект с учётом результатов этого воздействия, называется управлением по замкнутому циклу (или управление по принципу обратной связи). Иногда используется термин управление по отклонению. А САУ называется разомкнутой.
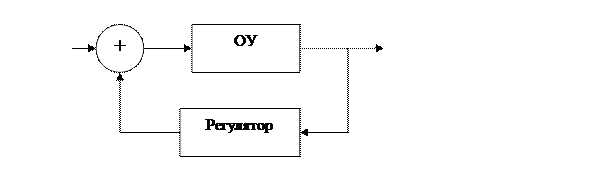
Рис. 4. 
Классификация регуляторов
Простейшими законами регулирования являются:
1. Пропорциональный закон
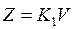 , где
, где 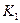 - коэффициент передачи. В этом случае говорят САУ с П-регулятором.
- коэффициент передачи. В этом случае говорят САУ с П-регулятором.
2. Интегральный закон 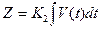 . CАУ с И-регулятором.
. CАУ с И-регулятором.
3. Дифференциальный закон 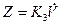 . САУ с Д –регулятором.
. САУ с Д –регулятором.
Возможны различные сочетания рассматриваемых вариантов регулирования ПИ, ПИД-регуляторы.
Дата добавления: 2016-06-02; просмотров: 748;
