Согласованный фильтр

В разделе 3 введенное понятие «согласованный фильтр» (СФ) как устройство для вычисления коэффициента представления демодулируемого сигнала в ортонормированном базисе. СФ находит более широкое применение в аппаратуре систем передачи. Поэтому ниже рассматривается СФ из общих позиций.

Есть линейный четырехполюсник (фильтр) с передаточной функцией H(jw). На его вход подается сумма детерминированного импульсного сигнала s(t) и помехи n(t): z(t) = s(t) + n(t). На выходе четырехполюсника имеет место сумма откликов на сигнал и помеху y(t) = y_s(t) + y_n(t). К выходу четырехполюсника подключен дискретизатор для взятия отсчета в момент t₀ (рис. 4.1). Такое устройство используется для ослабления помехи и взятия отсчета с целью определения амплитудного значения импульса s(t).

Фильтр называется согласованным с сигналом s(t), если при подаче на его вход суммы сигнала s(t) и помехи n(t) на его выходе в определенный момент времени t₀ имеет место максимальное отношение мгновенной мощности сигнала y_s²(t₀) к средней мощности шума P_{n вых}.

Согласованный фильтр (СФ) используется не только для максимального ослабления помехи, но и для выполнения некоторых других важных преобразований сигналов и помех. Поэтому рассмотрим свойства УФ.

1. Найдем передаточную функцию H(jw). Сигнал s(t) задан, а помеха n(t) – белый шум со спектральной плотностью мощности N₀/2.

Пусть

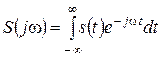– (4.1)

спектральная плотность сигнала s(t). Тогда спектральная плотность выходного сигнала y_s(t) определяется

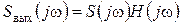. (4.2)

Отсчетное значение сигнала y_s(t₀) определим как обратное преобразование Фурье от S_вых(jw) для момента времени t₀

. (4.3)

Мощность шума на выходе фильтра (средний квадрат отсчета шума y_n(t₀)) определяются

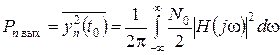. (4.4)

Запишем отношение мгновенной мощности сигнала y_s²(t₀) к средней мощности шума P_{n вых} в отсчетный момент

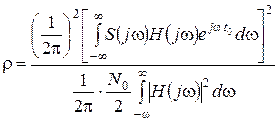. (4.5)

Будем искать передаточную функцию H(jw), при которой имеет место максимальное значение числителя в соотношении (4.5). Воспользуемся тем, что интеграл в числителе – скалярное произведение двух функций S*(jw) и 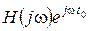(S*(jw) – функция, комплексно спряженная с функцией S(jw)). Скалярное произведение функций максимальное, если функции совпадают с точностью до произвольного положительного коэффициента c, т.е. 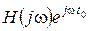= с×S*(jw). Значит, максимум числителя (4.5) имеет место при передаточной функции

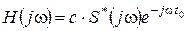. (4.6)

После подстановки выражения (4.6) в соотношение (4.5) получим

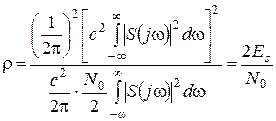. (4.7)

Здесь использовано, что энергия сигнала s(t) определяется

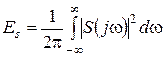. (4.8)

Видим, что при выполнении соотношения (4.6) обеспечивается не только максимум числителя отношения сигнал/шум (4.5), но и максимум этого отношения (значение r не зависит от конкретного вида передаточной функции H(jw), входящей в знаменатель). Таким образом, задача определения передаточной функции СФ H(jw) решена.

2. Соотношение (4.7) определяет максимально возможное отношение сигнал/шум на выходе фильтра в отсчетный момент. Это отношение принято называть пиковым

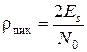. (4.9)

Определим выигрыш в отношении сигнал/шум, показывающий во сколько раз увеличивается отношение сигнал/шум при фильтрации СФ,

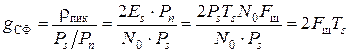, (4.10)

где F_ш – шумовая полоса помехи на входе фильтра;

T_s – длительность сигнала s(t);

P_s и P_n – средние мощности сигнала и помехи на входе фильтра.

Из выражения (4.10) видно, что при определенных соотношениях между шумовой полосой помехи и длительностью сигнала выигрыш может принимать большие значения.

3. Найдем амплитудно-частотную и фазочастотную характеристики СФ. Передаточная функция любой линейной электрической цепи определяет ее АЧХ и ФЧХ:

H(jw) = H(w) eхр(jj(w)), (4.11)

где H(w) – АЧХ цепи, j(w) – ФЧХ цепи.

Представим спектральную плотность сигнала s(t) через модуль и аргумент

S(jw) = S(w) exp(jy(w)), (4.12)

где S(w) – амплитудный спектр сигнала, y(w) – фазовый спектр сигнала.

После подстановки (4.11) и (4.12) в (4.6) получим, что АЧХ УФ

H(w) = сS(w) (4.13)

с точностью до произвольного коэффициента совпадает с амплитудным спектром сигнала, с которым фильтр согласован. Коэффициент передачи CФ больше на тех частотах, на которых больше составляющие сигнала s(t).

Равенство аргументов левой и правой частей (4.6) дает

j(w) = –y(w) – wt₀, (4.14)

что трактуется так: ФЧХ СФ с точностью до линейного слагаемого противоположна по знаку фазовому спектру сигнала, с которым фильтр согласован.

Для выяснения физической сущности ФЧХ СФ рассмотрим некоторую составляющую сигнала частоты f_i: A_icos(2pf_i t+ y_i). Эта составляющая на выходе CФ определяется:

A_i(f_i)cos(2pf_it+ y_i + j(f_i)) = A_i(f_i)cos(2pf_it + y_i – y_i – 2pf_it₀).

Полная фаза колебания равняется 2pf_i(t – t₀). В момент t = t₀ полная фаза колебания равна нулю независимо от частоты. В этот момент все составляющие находятся в фазе и при сложении дают максимально возможное значение отклика.

4. Найдем импульсную реакцию СФ как обратное преобразование Фурье от передаточной функции

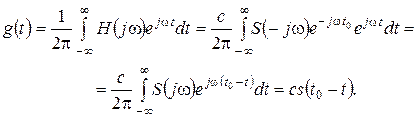(4.15)

Видим, что импульсная реакция СФ является зеркальным отображением сигнала, с которым фильтр согласован, относительно точки t₀ в масштабе с.

Пример 4.1. Построим график импульсной реакции фильтра, согласованного с сигналом

Условием физической реализуемости линейной электрической цепи является требование к ее импульсной реакции: g(t) º 0 для значений t < 0. Из рис. 4.2 видно, что для выполнения этого условия необходимо наложить требование на момент отсчета: t₀ ³ T_s, где T_s – длительность сигнала s(t).

а

5. Пусть на входе СФ действует произвольный сигнал z(t). Отклик фильтра определяется интегралом Дюамеля

, (4.16)

где K_zs(t) – функция взаимной корреляции сигналов z(t) и s(t).

Из выражения (4.16) вытекает, что форма сигнала на выходе СФ определяется функцией взаимной корреляции входного сигнала и сигнала, с которым фильтр согласован, а именно, она повторяет функцию взаимной корреляции в масштабе с и смещена вправо на t₀.

Если в соотношении (4.16) положить с = 1 и t₀ = T_s, то легко убедиться, что y(T_s) дает значение скалярного произведения сигналов z(t) и s(t). Это свойство СФ использовалась выше для определения коэффициентов разложения – соотношение (3.4).

6. Пусть на вход СФ подается сигнал, с которым фильтр согласован. Тогда на основании (4.16) запишем

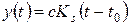, (4.17)

где K_s(t) – функция корреляции сигнала s(t).

Таким образом, если на вход СФ подается сигнал, с которым фильтр согласован, то отклик фильтра определяется функцией корреляции сигнала, а именно, она повторяет функцию корреляции сигнала в масштабе с и смещена вправо на t₀.

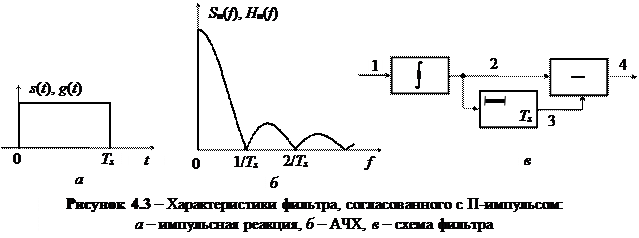
Упражнение 4.1. Проиллюстрируем рассмотренные свойства СФ на примере фильтра, согласованного с прямоугольным импульсом амплитуды А и длительности T_s. Пусть с = 1/A и t₀ = T_s. Импульсная реакция фильтра, согласованного с П-импульсом, имеет П-образную форму, амплитуду 1 и длительность T_s, т.е. импульсная реакция совпадает с сигналом (рис. 4.3, а).

Спектральная плотность П-импульса определяется преобразованием Фурье

S_п(jw) = 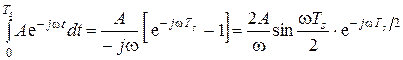. (4.18)

На основе соотношения (4.6) получим выражение для передаточной функции фильтра, согласованного с П-импульсом, если с = 1/A и t₀ = T_s

H(jw) = 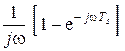. (4.19)

Из этого соотношения вытекает, что схема фильтра, согласованного с П‑импульсом, состоит из интегратора (с передаточной функцией 1/jw), устройства задержки на время T_s (с передаточной функцией exp(–jwT_s)) и вычитателя (рис. 4.3, в). На этом рисунке цифрами обозначены отдельные точки схемы для обсуждения ее работы.

Легко получить выражение для АЧХ фильтра, согласованного с П‑импульсом. Окончательное выражение для АЧХ после перехода к сменной f имеет вид функции sin(x)/x

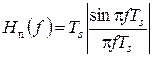. (4.20)

АЧХ СФ и амплитудный спектр сигнала показаны на рис 4.3, б.

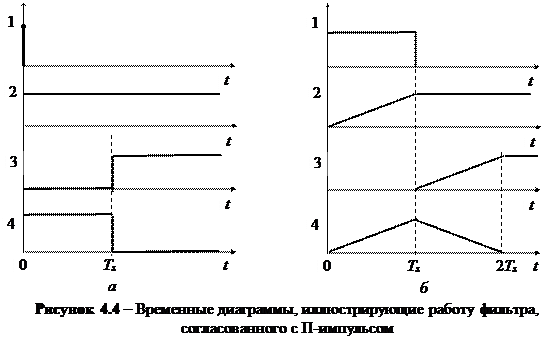
На рис. 4.4, а показаны процессы, имеющие место в СФ при подаче на его вход d-функции. На выходе схемы наблюдается импульсная реакция. На рис. 4.4, б показаны процессы, имеющие место в СФ при подаче на его вход импульса, с которым фильтр согласован. На выходе схемы наблюдается отклик, совпадающий с корреляционной функцией П-импульса длительностью Т_s (см. модуль 1).

Контрольные вопросы

1. Что является критерием оптимальности согласованного фильтра?

2. Пересчитайте свойства согласованного фильтра.

3. Как определяется пиковое отношение сигнал/шум на выходе согласованного фильтра?