Тренировочные задания
1. Уравнение ТП (1.1.2) для m = 1 имеет вид
St = a St-1 + b Ct + Ht ,
Предположим, что данное уравнение описывает рост биомассы (концентрации) S некоторого основного ингредиента вещества под воздействием дополнительного ингредиента вещества, имеющего концентрацию C. Пусть в начале процесса концентрация основного вещества равна S0, а концентрация дополнительного ингредиента равна C0. При этом концентрация дополнительного ингредиента убывает со временем t (t = 1, 2, 3, … T) по линейному закону
C t = C0 – g t.
Покажите, что зависимость St от b, C0 , g и T при a = 1 выражается как
ST = S0 + b C0 T – bg T (T +1)/2 +  .
.
Указание. Воспользуйтесь последовательной подстановкой значений t = 1, 2, 3, … T в уравнение ТП и формулой суммы членов арифметической прогрессии 1+2+3+… +T = T (T +1)/2.
2. Покажите, что зависимость St от b, C0 , g и T при произвольном a выражается как
ST = a T S0 +b C0[1+a +a2 +…+a T-1]–
– bg [a T-1+2a T-2+3a T-3 +…+(T–1)a + T] +  .
.
3. Преобразуйте полученное в 2 выражение, воспользовавшись формулой геометрической прогрессии
a 0 + a1 + a2 + … + a T-1 = 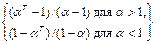 .
.
4. Найдите значение концентрации S основного ингредиента к моменту исчезновения дополнительного ингредиента при a = 1. Покажите при каких значениях g будет наблюдаться прирост концентрации основного ингредиента.
5. Дайте объяснение полученной модели ТП и смысла коэйффициентов a, b и g. Постройте примерную диаграмму ТП (см. рис.1.2.1).
6. Воспользовавшись правилом расчета дисперсий (см. стр. 27) покажите, что для úaú < 1 ошибка (дисперсия sS2 = = var(S)) определения ТП St имеет вид
var(S) = [b 2 g 2 T 2 /12+ sH2]/(1–a2),
если помеха некоррелирована c ТП, т.е., cov(St, Ht) = 0и cov(Сt, Ht) = 0, а такжеимеет дисперсию var(Ht, Ht) = sH2.
Указание. var(t) = T 2 /12.
Дата добавления: 2016-06-02; просмотров: 634;
