Напряженность магнитного поля

Ротор результирующего поля в магнетике

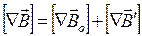. (19.3)

Учтем, что ротор внешнего поля 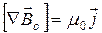определяется плотностью макроскопического тока 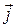. Аналогичное соотношение справедливо и для поля создаваемого магнетиком:

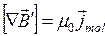. (19.3)

где 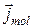- плотность молекулярных токов.

Аналогично тому, как для описания электриРческого поля в диэлектриках ис­пользуется вспомогательная величина – вектор электрической индукции 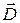, для описания магнитного поля в магне­тиках используется напряженность электрического поля 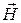. Чтобы сфор­мулировать ее определение необхо­димо выразить плотность молеку­лярных токов через вектор намагни­ченности 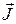. С этой целью найдем по­ток плотности молекулярных токов через неко­торую поверхность 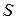, опирающуюся на контур 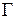(рисунок 19.1). При этом необходимо учесть, что поток соз­дают только токи, нанизанные на контур 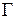. Другие токи либо не пересекают поверхность вовсе, либо пересекают ее дважды в противоположных направлениях, и потока создать не могут.

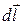На элемент контура нанизываются те токи, центры которых попадают внутрь косого цилиндра с высотой 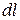и основанием, равным площади молекулярного тока 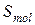. Объем такого цилиндра равен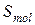 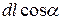. Если концентрация молекулярных токов 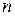, то в этот объем попадают токи

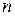
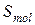
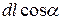(19.4)

токов, и суммарный поток, создаваемый ими равен:

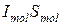
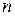
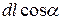, (19.5)

где 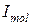- сила молекулярного тока.

Теперь необходимо учесть, что произведение 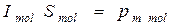– магнитному моменту молекулярного тока. А его произведение на концентрацию дает магнитный момент единицы объема, т.е. модуль вектора намагниченности. Поэтому поток, создаваемый молекулярными токами, нанизанными на элемент 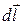контура, оказывается равным:

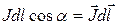(19.6)

Соответственно поток плотности молекулярных токов через всю поверхность 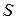оказывается равным циркуляции вектора намагниченности по контуру :

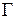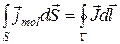(19.7)

По теореме Стокса

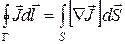, (19.8)

а значит

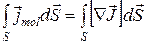. (19.9)

Таким образом,

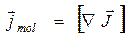. (19.10)

Теперь приходим к следующему соотношению для ротора результирующего поля в магнетике Объединим роторы

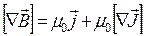. (19.11)

Объединим роторы в (19.11) и получим, что

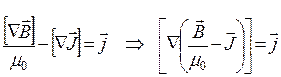. (19.12)

Ротор величины, в круглых скобках в (19.12) определяется плотностью только макроскопических токов, и ее, по определению, называют напряженностью магнитного поля:

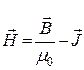. (19.13)