Для сипких грунтів можна записати
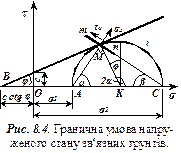
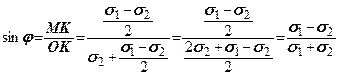 (8.1)
(8.1)
Для зв’язних грунтів
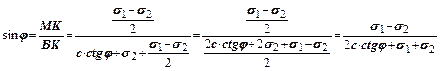 (8.2)
(8.2)
Рівняння (8.1) і (8.2) є умовами граничної рівноваги відповідно сипких і зв’язних грунтів. Граничний стан наступить у тих точках масиву, в яких будуть мати місце ці співвідношення.
Якщо з‘єднати точку М (рис. 8.4) з кінцем від-різка 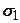 , то напрям МС визначить напрям площад-ки ковзання. З рис. 8.4 видно, що
, то напрям МС визначить напрям площад-ки ковзання. З рис. 8.4 видно, що 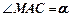 , а
, а 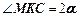 (виходячи з того, що
(виходячи з того, що 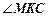 опирається на діаметр круга і охоплює ту ж дугу
опирається на діаметр круга і охоплює ту ж дугу 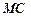 що й кут
що й кут 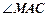 , який опирається на це ж коло Мора). Крім того,
, який опирається на це ж коло Мора). Крім того, 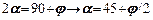 . З
. З  маємо
маємо 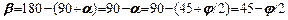 .Отже, зсув буде відбуватись на ділянках, нормаль яких відхилена на кут
.Отже, зсув буде відбуватись на ділянках, нормаль яких відхилена на кут 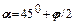 від напрямку
від напрямку 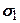 , або кут між ділянкою ковзання і напруженнями
, або кут між ділянкою ковзання і напруженнями 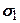 становить
становить 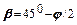 . В зв‘язку з тим, що головні площадки перпендикулярні одна одній (
. В зв‘язку з тим, що головні площадки перпендикулярні одна одній ( 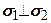 ) кут нахилу площадки ковзання до другої головної площадки буде дорівнювати
) кут нахилу площадки ковзання до другої головної площадки буде дорівнювати 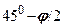 . Таким чином, в кожній точці грунтового середовища , яке перебуває в граничному стані, знаходиться дві площадки ковзання, які розташовані під кутом
. Таким чином, в кожній точці грунтового середовища , яке перебуває в граничному стані, знаходиться дві площадки ковзання, які розташовані під кутом 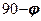 і
і 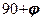 у відношенні одна до одної, що добре підтверджується стабілометричними дослідженнями.
у відношенні одна до одної, що добре підтверджується стабілометричними дослідженнями.
2. Розрахунковий опір грунту. Тиск 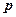 , при якому крива залежності
, при якому крива залежності 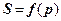 (рис. 7.2) умовно переходить від прямолінійної ділянки до криволінійної (кінець ІІ-ї, початок ІІІ-ї фази) називається розрахунковим опором грунту
(рис. 7.2) умовно переходить від прямолінійної ділянки до криволінійної (кінець ІІ-ї, початок ІІІ-ї фази) називається розрахунковим опором грунту  або першим критичним тиском
або першим критичним тиском 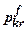 . Це навантаження є цілком безпечним, тому що зони граничного стану будуть займати незначні області під сторонами фундаменту і грунт практично знаходиться в фазі ущільнення.
. Це навантаження є цілком безпечним, тому що зони граничного стану будуть займати незначні області під сторонами фундаменту і грунт практично знаходиться в фазі ущільнення. 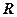 є максимальним тиском (навантаженням), при якому можна використовувати для розрахунків осідань фундаментів лінійні залежності між деформаціями і напруженнями. Якщо
є максимальним тиском (навантаженням), при якому можна використовувати для розрахунків осідань фундаментів лінійні залежності між деформаціями і напруженнями. Якщо 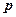 перевищує
перевищує 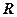 , то для визначення осідань фундаментів необхідно використовувати залежності, що враховують криволінійність функції
, то для визначення осідань фундаментів необхідно використовувати залежності, що враховують криволінійність функції 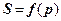 .
.
 Задача з визначення першого критичного тиску розв’язана М.П.Пузиревським у 1929р. Розглянемо дію рівномірно розподіленого навантаження
Задача з визначення першого критичного тиску розв’язана М.П.Пузиревським у 1929р. Розглянемо дію рівномірно розподіленого навантаження 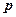 на смузі шириною
на смузі шириною 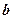 при наявності бічного завантаження
при наявності бічного завантаження 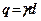 , викликаного заглибленням фундаменту на величину
, викликаного заглибленням фундаменту на величину 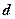 (рис. 8.5). Вертикальні стискуючі напруження від власної ваги грунту
(рис. 8.5). Вертикальні стискуючі напруження від власної ваги грунту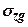 у точці
у точці 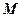 на глибині
на глибині 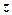 нижче підошви фундамету становлять
нижче підошви фундамету становлять
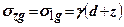 , де (8.3)
, де (8.3)
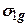 - головні напруження, викликані власною вагою грунту.
- головні напруження, викликані власною вагою грунту.
Приймемо припущення про гідростатичний розподіл напружень від власної ваги грунту, тобто 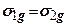 (в певній мірі це неправильно -
(в певній мірі це неправильно - 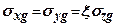 (7.24)).
(7.24)).
Вище було показано, що в умовах плоскої задачі величини головних напружень від дії навантаження 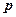 визначаються за формулами (7.21), (7.22)
визначаються за формулами (7.21), (7.22)
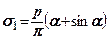 ;
; 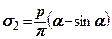
Для будь-якої точки  запишемо величини головних напружень, викликаних дією тиску
запишемо величини головних напружень, викликаних дією тиску  з урахуванням власної ваги грунту, використовуючи (7.21), (7.22)
з урахуванням власної ваги грунту, використовуючи (7.21), (7.22)
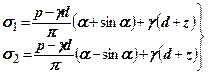 (8.4)
(8.4)
Зменшення 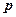 на величину
на величину 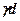 в (8.4) викликане заглибленням фундаменту.
в (8.4) викликане заглибленням фундаменту.
Підставимо (8.4) в умову граничної рівноваги зв’язного грунту (8.2) 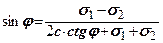 і розв’яжемо це рівняння відносно
і розв’яжемо це рівняння відносно 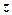
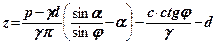 (8.5)
(8.5)
Знайдемо максимальну глибину розподілу зон граничної рівноваги 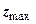 при навантаженні
при навантаженні 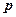 . Для цього похідну
. Для цього похідну 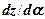 прирівняємо до
прирівняємо до 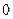
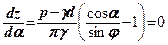 (8.6)
(8.6)
Умова (8.6) буде виконуватись коли 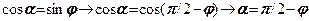 , або
, або 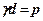 . Підставимо
. Підставимо 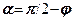 в (8.5)
в (8.5)
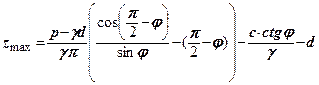 (8.7)
(8.7)
Розв’яжемо (8.7) відносно 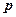
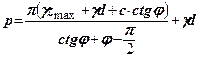 (8.8)
(8.8)
Як видно, рівняння (8.8) має два невідомих 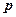 і
і 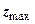 . Якщо прийняти
. Якщо прийняти 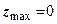 , тобто зовсім не допускати розповсюдження зон граничної рівноваги під підошвою фундаменту, тоді (8.8) прийме вигляд
, тобто зовсім не допускати розповсюдження зон граничної рівноваги під підошвою фундаменту, тоді (8.8) прийме вигляд
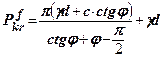 (8.9)
(8.9)
Діючі норми допускають розповсюдження зон зсувів на глибину 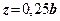 . При цьому вважається, що при такій умові залежність
. При цьому вважається, що при такій умові залежність 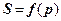 ще залишається близькою до лінійної. З урахуванням останнього можна записати
ще залишається близькою до лінійної. З урахуванням останнього можна записати
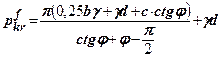 (8.10)
(8.10)
Позначимо: 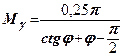 ;
; 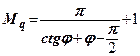 ;
; 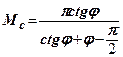
Тоді
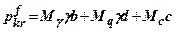 (8.11)
(8.11)
Коефіцієнти 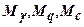 залежать тільки від кута внутрішнього тертя грунту і визначаються за допомогою спеціальних таблиць, вміщених в будівельних нормах. Крім того, формула (7) СНиП 2.02.01-83 [24] враховує додатково вид грунту, особливості будівлі, метод визначення характеристик міцності, ширину фундаменту, наявність підвалу і різницю в питомій вазі грунту. Ця формула має вигляд
залежать тільки від кута внутрішнього тертя грунту і визначаються за допомогою спеціальних таблиць, вміщених в будівельних нормах. Крім того, формула (7) СНиП 2.02.01-83 [24] враховує додатково вид грунту, особливості будівлі, метод визначення характеристик міцності, ширину фундаменту, наявність підвалу і різницю в питомій вазі грунту. Ця формула має вигляд
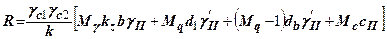 , (8.12)
, (8.12)
де 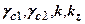 - коефіцієнти, які відповідно враховують вид грунту, споруди, метод визначення
- коефіцієнти, які відповідно враховують вид грунту, споруди, метод визначення 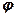 і
і 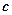 , ширину фундаменту;
, ширину фундаменту; 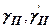 -питома вага грунту відповідно нижче і вище підошви фундаменту;
-питома вага грунту відповідно нижче і вище підошви фундаменту; 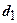 - глибина закладення фундаменту від підлоги підвалу;
- глибина закладення фундаменту від підлоги підвалу; 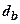 - глибина підвалу від рівня планувальної відмітки. Член
- глибина підвалу від рівня планувальної відмітки. Член 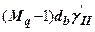 враховує наявність підвалу. При його відсутності
враховує наявність підвалу. При його відсутності  .
.
3. Несуча здатність грунтів.При дії тиску, який відповідає розрахунковому опору грунту, зони зсувів розповсюджуються на глибину, що дорівнює приблизно чверті ширини підошви фундаменту. При збільшенні навантаження область зсувів буде розширюватись і в деякий момент досягне ширини підошви фундаменту – відбудеться провальне осідання фундаменту з випором грунту. Таке навантаження називається другим критичним 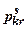 .
.
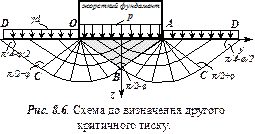 Розв‘язання диференційних рівнянь рівноваги сумісно з умовами граничної рівноваги дозволяє знайти точні обриси поверхні ковзання, використовуючи які можна достатньо точно знайти граничний тиск на грунт, який відповідає його максимальній несучій здатності.
Розв‘язання диференційних рівнянь рівноваги сумісно з умовами граничної рівноваги дозволяє знайти точні обриси поверхні ковзання, використовуючи які можна достатньо точно знайти граничний тиск на грунт, який відповідає його максимальній несучій здатності.
Припустивши, що нижче підошви фундаменту залягає невагомий грунт (  ), можна побудувати поверхні ковзання для смугоподібного рівномірно розподіленого навантаження, виходячи з того, що вони відхилені від напрямку більших головних напружень на кут
), можна побудувати поверхні ковзання для смугоподібного рівномірно розподіленого навантаження, виходячи з того, що вони відхилені від напрямку більших головних напружень на кут 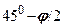 . У цьому випадку безпосередньо під фундаментом два ряди перетнутих поверхонь ковзання утворюють в зоні ОАВ вертикальні ромби (рис. 8.6). У зоні ОВС один ряд поверхонь ковзання утворює прямі лінії, що розходяться від точки О, а другий – логарифмічні спіралі. Далі в зоні ОСD також утворюються ромби, але горизонтальні, тому що в цій зоні найбільше головне напруження має горизонтальний напрям. Якщо враховувати власну вагу грунту, то побудова поверхонь ковзання значно ускладнюється. Вона стає ще складнішою при врахуванні жорсткості фундаменту та тертя по його підошві.
. У цьому випадку безпосередньо під фундаментом два ряди перетнутих поверхонь ковзання утворюють в зоні ОАВ вертикальні ромби (рис. 8.6). У зоні ОВС один ряд поверхонь ковзання утворює прямі лінії, що розходяться від точки О, а другий – логарифмічні спіралі. Далі в зоні ОСD також утворюються ромби, але горизонтальні, тому що в цій зоні найбільше головне напруження має горизонтальний напрям. Якщо враховувати власну вагу грунту, то побудова поверхонь ковзання значно ускладнюється. Вона стає ще складнішою при врахуванні жорсткості фундаменту та тертя по його підошві.
Задачу по визначенню 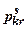 для рівномірно розподіленого навантаження по смузі (плоска задача) розв‘язав В.В.Соколовський, а для просторової – В.Г.Березанцев. Вираз для другого критичного тиску на грунт має вигляд
для рівномірно розподіленого навантаження по смузі (плоска задача) розв‘язав В.В.Соколовський, а для просторової – В.Г.Березанцев. Вираз для другого критичного тиску на грунт має вигляд
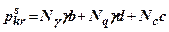 (8.13)
(8.13)
Як бачимо, вираз (8.13) є подібним до виразу (8.11), тобто формули для визначення першого і другого критичного тисків відрізняються лише значеннями сталих коефіцієнтів.
Для розрахунку несучої здатності основи фундаменту СНиП 2.02.01-83 [24] пропонує такий вираз (формула 16)
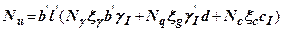 , де (8.14)
, де (8.14)
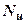 - вертикальна складова сили граничного опору грунту;
- вертикальна складова сили граничного опору грунту; 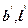 - приведена ширина і довжина підошви фундамента, що визначаються за формулами
- приведена ширина і довжина підошви фундамента, що визначаються за формулами 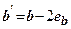 ;
; 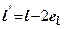 ,
,
де 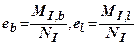 - відповідно ексцентриситети передачі навантажень в поперечному і поздовжньому напрямку.
- відповідно ексцентриситети передачі навантажень в поперечному і поздовжньому напрямку.
 Символом
Символом 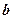 позначена сторона фундамента, в напрямку якої припускається втрата стійкості основи.
позначена сторона фундамента, в напрямку якої припускається втрата стійкості основи.
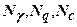 - безрозмірні коефіцієнти несучої здатності, визначаються за табл. 7 СНиП 2.02.01-83 залежно від кута внутрішнього тертя
- безрозмірні коефіцієнти несучої здатності, визначаються за табл. 7 СНиП 2.02.01-83 залежно від кута внутрішнього тертя 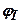 і
і 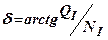 - кута нахилу рівнодіючої ТІ до вертикальної осі (рис. 8.7);
- кута нахилу рівнодіючої ТІ до вертикальної осі (рис. 8.7); 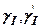 - питома вага грунту відповідно нижче (в межах можливої призми випирання) і вище підошви фундаменту;
- питома вага грунту відповідно нижче (в межах можливої призми випирання) і вище підошви фундаменту; 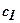 - питоме зчеплення грунту;
- питоме зчеплення грунту; 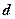 - глибина закладення фундаменту;
- глибина закладення фундаменту; 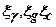 - коефіцієнти форми фундаменту, визначаються за формулами
- коефіцієнти форми фундаменту, визначаються за формулами
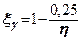 ;
; 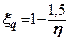 ;
; 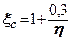 ,
,
де 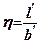 . Якщо
. Якщо 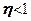 необхідно приймати
необхідно приймати 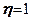 .
.
Суть розрахунків основ за несучої здатністю зводиться до визначення 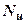 і порівняння його з вертикальною складовою сили, що передається на фундамент (див. п.2.58 [24]).
і порівняння його з вертикальною складовою сили, що передається на фундамент (див. п.2.58 [24]).
4. Стійкість грунтів в укосах.При влаштуванні котлованів, насипів, зведенні будівель на схилах необхідно перевіряти стійкість укосів. Порушення стійкості укосів у більшості випадків відбувається раптово із сповзанням значних мас грунту. Така втрата рівноваги грунтового масиву називається зсувом. Основні причини утворення зсувів такі: збільшення навантаження на укіс, зниження характеристик міцності грунтів, недопустимо круті укоси , тощо.
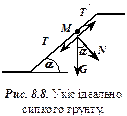 Ідеально сипкий грунт
Ідеально сипкий грунт  .Припустимо, що на укосі знаходиться тверда частинка
.Припустимо, що на укосі знаходиться тверда частинка  (рис. 8.8). Розкладемо вагу частинки
(рис. 8.8). Розкладемо вагу частинки  на нормальну до укосу
на нормальну до укосу 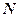 і дотичну
і дотичну 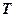 складові.
складові.
Сила 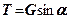 намагається зсунути частинку вниз, але їй протидіє сила тертя
намагається зсунути частинку вниз, але їй протидіє сила тертя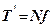 (
(  )
) 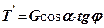 . В граничному стані
. В граничному стані 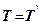 . Проектуємо всі сили на похилу грань
. Проектуємо всі сили на похилу грань
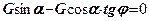 (8.15)
(8.15)
Звідки
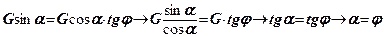 (8.16)
(8.16)
Отже, граничний кут укосу ідеально сипких грунтів 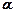 дорівнює їх куту внутрішнього тертя
дорівнює їх куту внутрішнього тертя 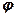 . Такий кут називається кутом природнього укосу.
. Такий кут називається кутом природнього укосу.
Ідеально зв‘язний грунт ( 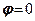 ). Припустимо, що порушення рівноваги для деякої висоти
). Припустимо, що порушення рівноваги для деякої висоти 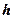 відбудеться вздовж поверхні ковзання
відбудеться вздовж поверхні ковзання 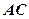 , нахиленої під кутом
, нахиленої під кутом 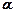 до горизонту (рис. 8.9). Враховуючи, що
до горизонту (рис. 8.9). Враховуючи, що 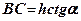 , вага сповзаючого відсіку буде
, вага сповзаючого відсіку буде
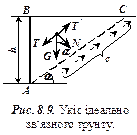
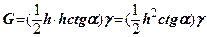 (8.17)
(8.17)
Розкладемо силу 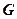 на нормальну і дотичну до поверхні ковзання
на нормальну і дотичну до поверхні ковзання 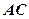 . Опір ковзанню створюють тільки сили зчеплення (
. Опір ковзанню створюють тільки сили зчеплення ( 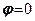 ), розподілені по площині ковзання
), розподілені по площині ковзання 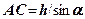 .
.
 Урахувавши те, що в верхній точці
Урахувавши те, що в верхній точці  призми зрушення
призми зрушення  тиск дорівнює нулю, а в нижній – максимальний, в середньому треба брати тільки половину величини сил зчеплення. Отже, утримуюча сила
тиск дорівнює нулю, а в нижній – максимальний, в середньому треба брати тільки половину величини сил зчеплення. Отже, утримуюча сила 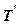 становитиме:
становитиме: 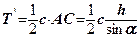 . Зсуваюча сила
. Зсуваюча сила 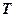 дорівнюватиме:
дорівнюватиме: 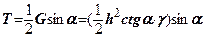 .
.
Складемо рівняння рівноваги, взявши суму проекцій усіх сил на напрямок 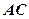 і прирівняємо їх до нуля
і прирівняємо їх до нуля
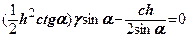 (8.18)
(8.18)
Звідки
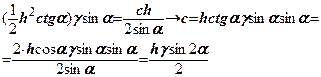 (8.19)
(8.19)
Знайдемо максимальне значення висоти 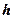 , при якій буде забезпечена стійкість вертикального укосу. У цьому випадку
, при якій буде забезпечена стійкість вертикального укосу. У цьому випадку 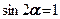 . Підставляючи у вираз (8.19)
. Підставляючи у вираз (8.19) 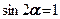 , після перетворень одержимо
, після перетворень одержимо
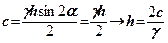 (8.20)
(8.20)
Наприклад, для грунту, який має питоме зчеплення 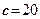 кПа і питому вагу
кПа і питому вагу 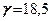 кН/м3 висота вертикального укосу
кН/м3 висота вертикального укосу 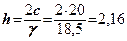 м.
м.
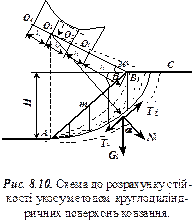
Метод круглоциліндричних поверхонь ковзання. В природних умовах грунти мають тертя і зчеплення, тому задача значно ускладнюється. В точній постановці вона розв’язана В.В.Соколовським, але ці розв’язки можна використовувати тільки для однорідних грунтів.
У практиці найширше застосовують наближений інженерний метод круглоциліндричних поверхонь ковзання. Суть методу полягає в слідуючому: в місцях можливої втрати стійкості грунту проводять круглоциліндричні поверхні, по яких може відбуватися зсув, і для кожного випадку визначають відношення утримуючих 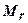 і зсуваючих
і зсуваючих 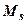 моментів сил (рис 8.10).
моментів сил (рис 8.10).
Зрушуюча сила: 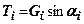 . Утримуючі сили:
. Утримуючі сили: 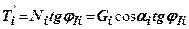 - сила, яка виникає за рахунок тертя;
- сила, яка виникає за рахунок тертя; 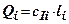 - сила, яка виникає за рахунок зчеплення. Тут
- сила, яка виникає за рахунок зчеплення. Тут 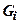 - вага і-го відсіку;
- вага і-го відсіку; 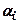 - кут нахилу поверхні ковзання і-го відсіку до горизонталі;
- кут нахилу поверхні ковзання і-го відсіку до горизонталі; 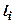 - довжина і-го відсіку.
- довжина і-го відсіку.
Сума моментів зрушуючих сил
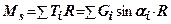 (8.21)
(8.21)
Дата добавления: 2016-06-02; просмотров: 690;
