Результаты расчетов параметров схемы замещения для номинального напряжения 110 кВ сводим в таблицу 1.14
Таблица 1.14 – Параметры схемы замещения (Uн = 110 кВ)
| Участок | Провод | n | r 0, Ом/км | x 0, Ом/км | b 0, мкСм/км | l, км | Rл, Ом | Xл, Ом | Bл, мкСм |
| 0-1 | АС-70 | 0,42 | 0,44 | 2,58 | 35,0 | 7,35 | 7,7 | 180,6 | |
| 0-2 | АС-70 | 0,42 | 0,44 | 2,58 | 35,0 | 7,35 | 7,7 | 180,6 | |
| 0-3 | АС-70 | 0,42 | 0,44 | 2,58 | 45,0 | 9,45 | 9,9 | 232,2 | |
| 3-4 | АС-70 | 0,42 | 0,44 | 2,58 | 40,0 | 16,8 | 17,6 | 103,2 | |
| 0-5 | АС-70 | 0,42 | 0,44 | 2,58 | 55,0 | 23,1 | 24,2 | 141,9 |
Потеря напряжения в % от номинального на участках сети в нормальном режиме
 Uij%=
Uij%= 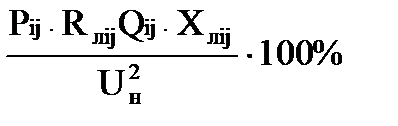 (1.27)
(1.27)
Для участка 0-1
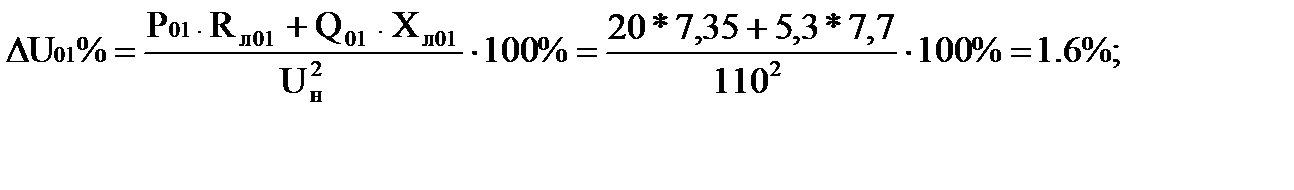
Потери напряжения на остальных участках определяем аналогично. Результаты сводим в таблицу 1.15.
Таблица 1.15 - Потери напряжения - нормальный режим 110 кВ
| Участок | Р, Мвт | Q, Мвар | R, Ом | X, Ом | ΔU кВ | ΔU % |
| 0-1 | 20,0 | 5,3 | 7,35 | 7,70 | 1,7 | 1,6 |
| 0-2 | 25,0 | 6,6 | 7,35 | 7,70 | 2,1 | 1,9 |
| 0-3 | 26,0 | 6,9 | 9,45 | 9,90 | 2,9 | 2,6 |
| 3-4 | 11,0 | 2,9 | 16,80 | 17,60 | 2,1 | 2,0 |
| 0-5 | 8,0 | 2,1 | 23,10 | 24,20 | 2,1 | 2,0 |
Для разомкнутых сетей потери напряжения в послеаварийном режиме на участках сети увеличиваются в n раз, так как при выходе из строя одной из цепи двухцепных участков сопротивление участка увеличивается в n раз
Потеря напряжения на участках сети в послеаварийном режиме
Uавij% =n Uij% (1.28)
Результаты расчетов по потери напряжения на участках сети в послеаварийном режиме сводим в таблицу 1.16.
Таблица 1.16 - Потери напряжения - послеаварийный режим 110 кВ
| Участок | Р, Мвт | Q, Мвар | Rл, Ом | Xл, Ом | ΔU кВ | ΔU % |
| 0-1 | 20,0 | 5,3 | 14,70 | 15,40 | 3,4 | 3,1 |
| 0-2 | 25,0 | 6,6 | 14,70 | 15,40 | 4,3 | 3,9 |
| 0-3 | 26,0 | 6,9 | 18,90 | 19,80 | 5,7 | 5,2 |
| 3-4 | 11,0 | 2,9 | 16,80 | 17,60 | 2,1 | 2,0 |
| 0-5 | 8,0 | 2,1 | 23,10 | 24,20 | 2,1 | 2,0 |
Проверка сети по потери напряжения осуществляется для точек электрически наиболее удаленных. В разомкнутых сетях такими точками являются все концевые точки сети.
В нашем случае это точки: 1, 2, 4 и 5
Условие проверки в нормальном режиме максимальных нагрузок:
 Uдоп%=³
Uдоп%=³  U%, (1.29)
U%, (1.29)
где  Uдоп% - допустимая величина потери напряжения (в % от номинального напряжения) в нормальном режиме.
Uдоп% - допустимая величина потери напряжения (в % от номинального напряжения) в нормальном режиме.
Пункты 1,2 и 5 как это видно из таблицы 1.13 удовлетворяют условию проверки по допустимой потери напряжения.
Проверяем по потери напряжения точку 4
 U034 =
U034 =  U03 +
U03 +  U34 = 2,6%+2,2% = 4,8 % ,
U34 = 2,6%+2,2% = 4,8 % ,
что меньше допустимой потери напряжения
Аналогично проверяют сеть в послеаварийном режиме:
 Uдоп.ав%³
Uдоп.ав%³  Uав%, (1.30)
Uав%, (1.30)
где  Uдоп.ав% - допустимая величина потери напряжения (в % от номинального напряжения) в послеаварийном режиме, которую для районных сетей можно принять равной (20¸25)%.
Uдоп.ав% - допустимая величина потери напряжения (в % от номинального напряжения) в послеаварийном режиме, которую для районных сетей можно принять равной (20¸25)%.
Пункты 1,2 и 5 как это видно из таблицы 1.14 удовлетворяют условию проверки по допустимой потери напряжения в послеаварийном режиме.
Проверяем по потери напряжения точку 4
 U034ав =
U034ав =  U03ав +
U03ав +  U34ав = 5,2+2,0 = 7,2 %
U34ав = 5,2+2,0 = 7,2 %
Сеть удовлетворяет условию проверки по потери напряжения в нормальном и послеаварийном режимах при напряжении 110 кВ.
Аналогично выполняется расчет для номинального напряжения 150 кВ.
Если сеть не удовлетворяет условию проверки по допустимой потери напряжения в нормальном или послеаварийном режимах, то из дальнейшего рассмотрения этот вариант следует исключить.
1.6.2 Расчет смешанного варианта сети.
1.6.2.1.Расчет потокораспределения в нормальном режиме максимальных нагрузок.
Расчет ведем без учета потерь мощности на участках сети.
1 Р01 5
Р12 РЭС
2 Р02 3
Рисунок 1.18
P01= 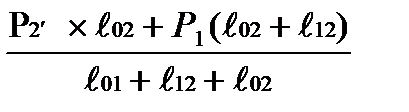 ;
;
P01= 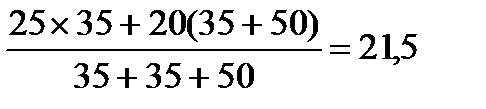 МВт ;
МВт ;
По первому закону Кирхгофа для узла 1 найдем Р12.
Р12= Р01-Р1
Р12= 21,5-20 = 1,5 МВт;
Далее аналогично находим Р02
Р02=Р2-Р12
Р02=25 –1,5 = 23,5 МВт
Проверка:
P02= 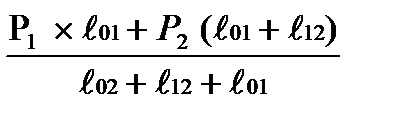 ;
;
P02= 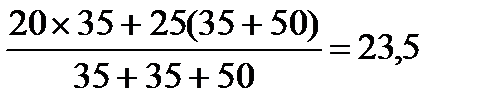 МВт ;
МВт ;
Реактивные нагрузки по участкам сети
Qij=Pij*tgср.взв.
Для участка 0-1
Q01=P01*tgср.взв.
Q01=21,5*0,264 =5,3Мвар
Полные нагрузки участков сети
Sij= 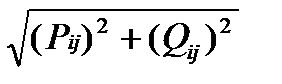 ;
;
Для участка 0-1
S01= 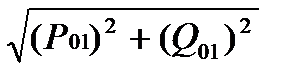 =
= 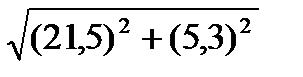 =20,7 МВА
=20,7 МВА
Аналогично рассчитываем участки 1-2 и 0-2. Для остальных участков потокораспределение берем из предыдущего варианта. Результаты вычислений заносим в таблицу 1.17
Таблица 1.17 Потокораспределение по ветвям сети
| Участок | 0-1 | 0-2 | 0-3 | 3-4 | 0-5 | 1-2 |
| Р, Мвт | 21,5 | 23,5 | 35,0 | 15,0 | 8,0 | 1,5 |
| Q, Мвар | 5,7 | 6,2 | 9,3 | 4,0 | 2,1 | 0,4 |
| S, МВА | 22,2 | 24,4 | 36,2 | 15,5 | 8,3 | 1,5 |
1.6.2.2. Выбор номинального напряжения сети
Выбор номинального напряжения производится так же как для предыдущего варианта.
Расчеты по выбору напряжения сети сведены в таблицу 1.18.
Таблица 1.18 – Выбор номинального напряжения сети
| Участок | 0-1 | 0-2 | 0-3 | 3-4 | 0-5 | 1-2 |
| l, км | 35,0 | 35,0 | 45,0 | 40,0 | 55,0 | 50,0 |
| Р, Мвт | 21,5 | 23,5 | 35,0 | 15,0 | 8,0 | 1,5 |
| Uор, кВ | 83,8 | 85,7 | 100,8 | 79,2 | 73,3 | 46,8 |
Принимаем для дальнейшего расчета два варианта:
1) номинальное напряжение Uн=110 кВ;
2) номинальное напряжение Uн=150 кВ.
1.6.2.3.Выбор сечения проводов ЛЭП.
Определяем рабочие токи участков сети. Для участка 0-1
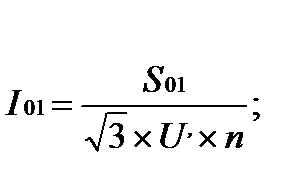
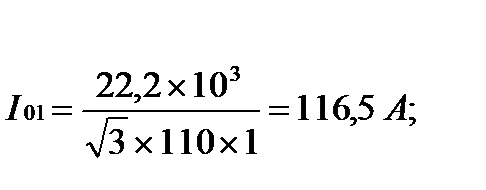
Определяем ориентировочные сечения по участкам сети. Для участка 0-1
Fop01= 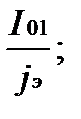
Fop01= 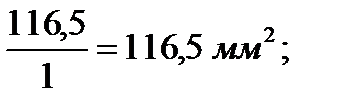
Принимаем для участка 0-1 стандартное сечение - Fст01= 120 мм2.
Аналогично определяем сечения на остальных участках сети, результаты вычислений заносим в таблицу 1.19.
Таблица 1.17 – Сечения участков сети, Uн = 110 кВ
| Участок | 0-1 | 0-2 | 0-3 | 3-4 | 0-5 | 1-2 |
| n | ||||||
| S, МВА | 22,2 | 24,4 | 36,2 | 15,5 | 8,3 | 1,5 |
| I | 116,5 | 127,8 | 95,0 | 81,4 | 43,4 | 7,9 |
| Fэ, мм2 | 116,5 | 127,8 | 95,0 | 81,4 | 43,4 | 7,9 |
| Fст, мм2 |
1.6.2.5 Проверка проводов по току наиболее тяжелого после аварийного режима.
Для кольцевых участков сети наиболее тяжелыми послеаварийными режимами работы сети являются - поочередное отключение головных участков 0-1 и 0-2
Проверку осуществим для кольцевого участка сети 0-1-2-0.
Расчет выполним для двух режимов:
а) Выход из строя головного участка 0-1
Потокораспределение активных нагрузок
P12ав=P1=20 МВт ;
Р02ав=Р1+Р2 =20+25= 45 МВт
б) Выход из строя головного участка 0-2
P12ав=P2=25МВт ;
Р01ав=Р1+Р2 =20+25=45 МВт ;
Для участка 1-2 в качестве наиболее тяжелого послеаварийного режима принимаем режим б), с наибольшей нагрузкой
Результаты проверки сводим в таблицу 1.20.
Таблица 1.20. – Проверка по допустимому току в послеаварийном режиме,
(Uн = 110 кВ)
| Участок | Рмах, МВт | I ав, А | F, мм2 | Iдоп, А | Fприн, мм2 |
| 0-1 | 251,47 | ||||
| 0-2 | 251,47 | ||||
| 1-2 | 139,7 |
1.6.2.6.Проверка сети по потери напряжения в нормальном и после аварийном режиме.
Определяем параметры схемы замещения ЛЭП.
Результаты сводим в таблицу 1.21.
Таблица 1.21 –Параметры схемы замещения сети, Uн = 110 кВ
| Участок | Провод | n | r0, Ом/км | x0, Ом/км | b0, мкСм/км | l, км | Rл, Ом | Xл, Ом | Bл, мкСм |
| 0-1 | АС-120 | 0,249 | 0,423 | 2,69 | 8,72 | 14,81 | 94,15 | ||
| 0-2 | АС-120 | 0,249 | 0,423 | 2,69 | 8,72 | 14,81 | 94,15 | ||
| 0-3 | АС-95 | 0,314 | 0,429 | 2,65 | 7,06 | 9,65 | 238,5 | ||
| 3-4 | АС-70 | 0,42 | 0,44 | 2,58 | 16,8 | 17,6 | 103,2 | ||
| 0-5 | АС-70 | 0,42 | 0,44 | 2,58 | 23,1 | 24,2 | 141,9 | ||
| 1-2 | АС-70 | 0,42 | 0,44 | 2,58 |
Расчет потерь напряжения на участках сети сведен в таблицу 1.22.
Таблица 1.22 -Потери напряжения - нормальный режим, Uн = 110 кВ
| Участок | Р | Q | Rл, Ом | Xл, Ом | ΔU кВ | ΔU % |
| 0-1 | 21,5 | 7,5 | 8,72 | 14,81 | 2,7 | 2,5 |
| 0-2 | 23,5 | 8,2 | 8,72 | 14,81 | 3,0 | 2,7 |
| 1-2 | 1,5 | 0,5 | 21,00 | 22,00 | 0,4 | 0,3 |
В кольцевом участке проверку по потери напряжения осуществляют до точки потокораздела, в нашем случае это точка 2.
 U012 =
U012 =  U01 +
U01 +  U12 = 2,5+0,3 = 2,8 %
U12 = 2,5+0,3 = 2,8 %
Потеря напряжения до точки 2 (точка потокораздела) не превышают допустимые
Аналогично определяем потери напряжения на участках сети для двух аварийных режимов а) и б). Результаты расчетов сводим в таблицы 1.21 и 1.22.
Для режима а) определяем  U021ав =
U021ав =  U02ав +
U02ав +  U12ав.
U12ав.
Для режима б)  U012ав =
U012ав =  U01ав +
U01ав +  U12ав
U12ав
Таблица 1.21-Потери напряжения - послеаварийный режим а), Uн = 110 кВ
| Участок | Р | Q | Rл, Ом | Xл, Ом | ΔU, кВ | ΔU % |
| 0-2 | 45,0 | 15,7 | 8,72 | 14,81 | 5,7 | 5,2 |
| 1-2 | 20,0 | 7,5 | 21,00 | 22,00 | 5,3 | 4,8 |
| Итого |
Таблица 1.22 - Потери напряжения - послеаварийный режим б), Uн = 110 кВ
| Участок | Р | Q | Rл, Ом | Xл, Ом | ΔU кВ | ΔU % |
| 0-1 | 45,0 | 15,7 | 8,72 | 14,81 | 5,7 | 5,2 |
| 1-2 | 25,0 | 8,2 | 21,00 | 22,00 | 6,4 | 5,8 |
| Итого |
Сеть удовлетворяет условию проверки по потере напряжения в послеаварийном режиме.
1.6.3 Расчет сложнозамкнутого варианта сети.
1.6.3.1 Расчет потокораспределения в нормальном режиме максимальных нагрузок
Расчет потокораспределения для сложнозамкнутого варианта сети может быть выполнен различными методами:
- с использованием законов Кирхгофа;
- методом контурных мощностей;
- методом узловых напряжений;
- методом последовательного преобразования схемы;
- прочими методами.
На раннем этапе проектирования, до определения сечений на участках сети, расчет выполняется без учета потерь, из предположения равенства сечений проводов по участкам, что позволяет в математической модели сети перейти от комплексно-сопряженных сопротивлений к длинам участков.
Кроме того, принятое в 1.31 распределение компенсирующих устройств позволяет вести расчеты потокораспределения по сети отдельно и независимо по активной и реактивной мощности.
Поэтому в дальнейших расчетах будем искать потокораспределение активной мощности. Потоки реактивных мощностей по ветвям сети легко находятся по выражению
Qij=Pij*tgφср.взв. (1.31)
Рассмотрим основные методы, применяемые для таких расчетов.
Пример 1.7Произвести расчет потокораспределения для схемы сети, показанной на рисунке 1.19.
Расчет ведем без учета потерь мощности на участках сети.
А) Расчет потокораспределения с использованием законов Кирхгофа
Наносим на схему ориентировочное потокораспределение Pij (Рисунок 1.19).
| Р01 |
| Р05 |
| Р03 |
| Р34 |
| Р12 |
| Р23 |
| Р02 |
| Р5 |
| Р4 |
| Р3 |
| Р1 |
| Р2 |
Рисунок 1.19
Расчет участка 0-5 выполняем независимо от режима остальной части сети:
Р05 = Р5 (1.32)
Определяем мощность на разомкнутом участке 3-4, примыкающего к сложнозамкнутой части сети
Р34 = Р4 (1.33)
| Р01 |
| Р03 |
| Р12 |
| Р23 |
| Р02 |
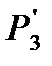 =Р3+Р4 =Р3+Р4
|
| Р1 |
| Р2 |
Рисунок 1.20 - Преобразованнапя схема
где 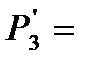 Р3 + Р34 = Р3 + Р4
Р3 + Р34 = Р3 + Р4
Определим топологические характеристики схемы сети:
- количество узлов n = 4;
- количество ветвей m = 5.
Тогда количество уравнений составляемых по 1-му закону Кирхгофа
k1 = n-1 =4-1=3
Количество уравнений составляемых по 2-му закону Кирхгофа
k2 =m-(n-1) =5-(4-1)=2
Таким образом составляем полную систему уравнений по законам Кирхгофа: три уравнения по 1-му закону (для произвольно выбираемых узлов) и два уравнения по 2-му закону для контуров (выберем в качестве независимых контуров контуры: 0-1-2-0 и 0-2-3-0.
узел 1: Р01 -Р12 =Р1
узел 2: Р02 +Р12 -Р23= Р2
узел 3: Р03+Р23 = Р3+Р4 (1.34)
контур 0-1-2-0: P01·l01 +P12·l12 - P02·l02 = 0
контур 0-2-3-0: P02·l02 +P23·l23 - P03·l03 = 0
Решим систему уравнений для следующих исходных данных:
Р1=20 МВт; Р2=25 МВт; Р3=15 МВт; Р4=11 МВт; Р5= 8 МВт;
l01= 35 км; l02= 35 км; l03= 45 км; l12= 50 км; l23= 60 км.
Расчет выполняем в среде Mathcad двумя способами, с помощью матриц и с помощью блока решений Given.
Решение показано на рисунке 1.21


Рисунок 1.21 - решение системы в среде Mahtcad
Покажем решение системы уравнений в MS Excel, рисунки 1.22 и 1.23
Это решение соответствует первому способу, показанному на рисунке 1.18.
Занесем в ячейки A3:E3 длины участков, а ячейки F3:I3 нагрузки Р1, Р2,Р3,Р4. В ячейки A6:E10 занесем матрицу коэффициентов системы - А, а в ячейки G6:G10 свободные члены системы - B.
Выделим блок B13:B17. В этом блоке активной будет ячейка B13. Наберем формулу =МУМНОЖ(МОБР(A6:E10);G6:G10). Нажмем сочетание клавиш Ctrl+Shift+Enter одновременно. В строке формул появится выражение {=МУМНОЖ(МОБР(A6:E10);G6:G10)} в фигурных скобках. Это свидетельствует о том, что формула стала табличной. Во всех ячейках выделенного блока появится формула =МУМНОЖ(МОБР(A6:E10);G6:G10), рисунок 1.22
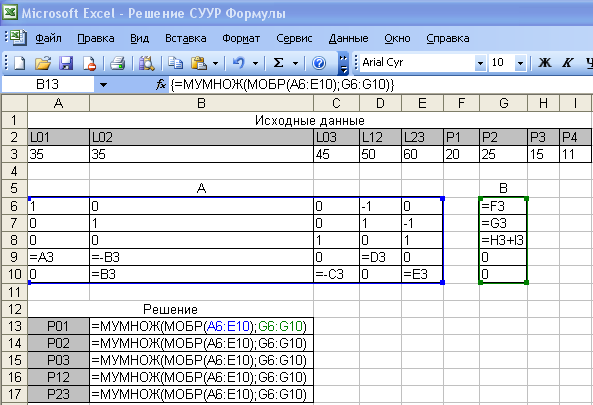
Рисунок 1.22 - лист Excel с отображением формул
На рисунке 1.23 представлено решение системы уравнений установившегося режима рассматриваемой сети. Значения потоков активной мощности по ветвям сети расположены в ячейках В13:В17.
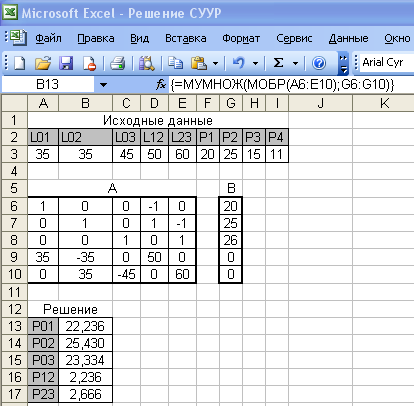
Рисунок 1.23 - лист Excel с решением
Б) Расчет потокораспределения методом контурных мощностей
Покажем расчет потокораспределения на преобразованной схеме, рисунок 1.20.
Количество контурных уравнений
kк =m-(n-1) =5-(4-1)=2
Выделим два независимых контура: 0-1-2-0 и 0-3-2-0.
Обозначим контурные мощности PI и PII.
| Р01 |
| Р03 |
| Р12 |
| Р23 |
| Р02 |
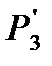
|
| Р1 |
| РI |
| РII |
Рисунок 1.24
Запишем систему контурных уравнений
контур 0-1-2-0: P01·l01 +P12·l12 - P02·l02 = 0
(1.35)
контур 0-3-2-0: P03·l03 -P02·l02 -P23·l23 = 0
Примем
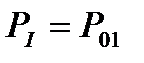 ;
; 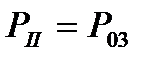 (1.36)
(1.36)
Выразим потоки мощности на остальных участках через контурные мощности, используя первый закон Кирхгофа
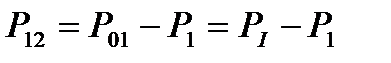
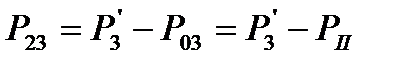 (1.37)
(1.37)
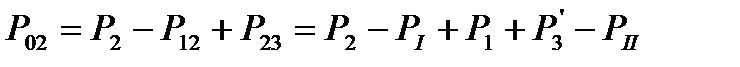
Подставим 1.36 и 1.37 в 1.35. Получим
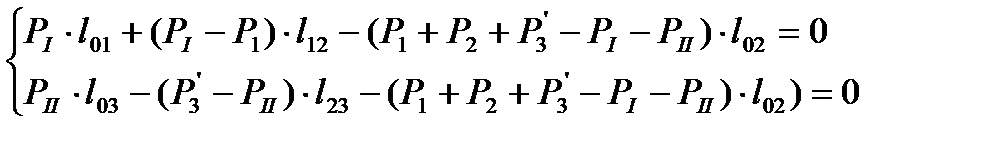 (1.38)
(1.38)
Преобразуем 1.38 к удобному для расчета виду
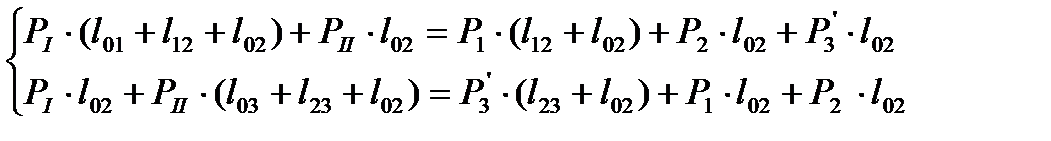 (1.39)
(1.39)
Решив систему 1.39, находим контурные мощности, при подстановке которых в 1.37 и 1.38 получаем потокораспределение по ветвям.
Пример 1.8Произвести расчет потокораспределения для схемы сети, показанной на рисунке 1.24 методом контурных мощностей для исходных данных, заданных в примере 1.17.
Подставляем исходные данные в систему 1.38
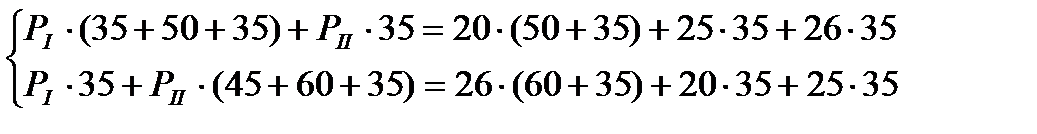
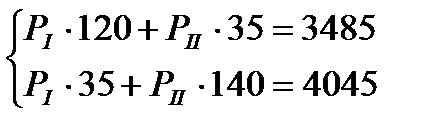
Решим систему с помощью теоремы Крамера.
Главный определитель системы
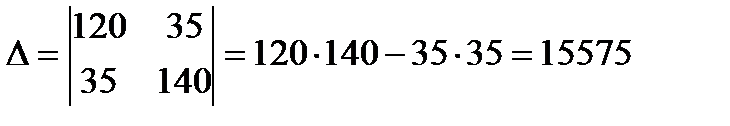
Вспомогательные определители
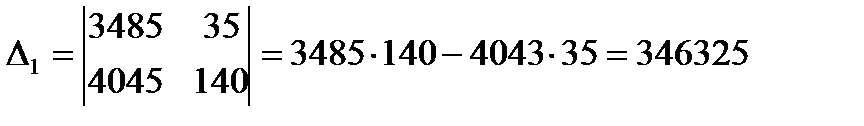
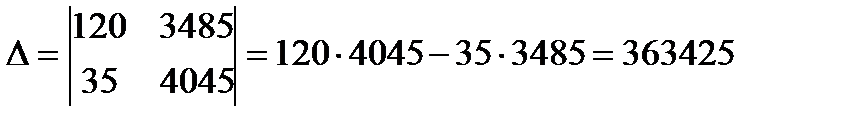
Решение системы
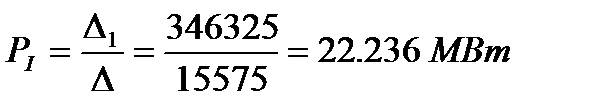
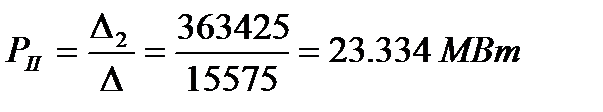
Находим потокораспределение по ветвям схемы
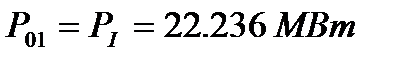
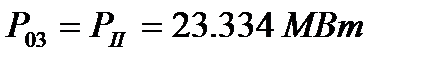
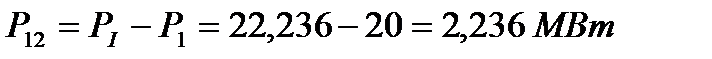
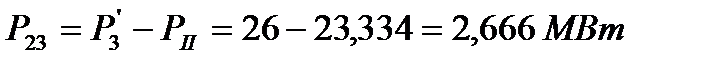
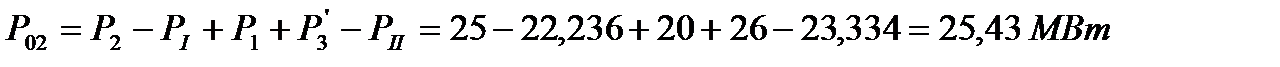
Г) Формирование системы контурных уравнений с использованием графов
Формирование системы контурных уравнений по выше изложенной методике приводит к трудоемким промежуточным вычислениям, особенно для задач большой размерности.
Вместе с тем система контурных уравнений может быть легко получена без промежуточных преобразований с использованием графов.
Порядок формирования системы контурных уравнений:
Формируем граф сети, дерево и хорды;
Выбираем систему независимых контуров таким образом, чтобы в каждый из них вошла одна из хорд;
Принимаем значение и направление мощностей в хордах соответствующим контурным мощностям;
Записываем систему контурных уравнений в формализованном виде
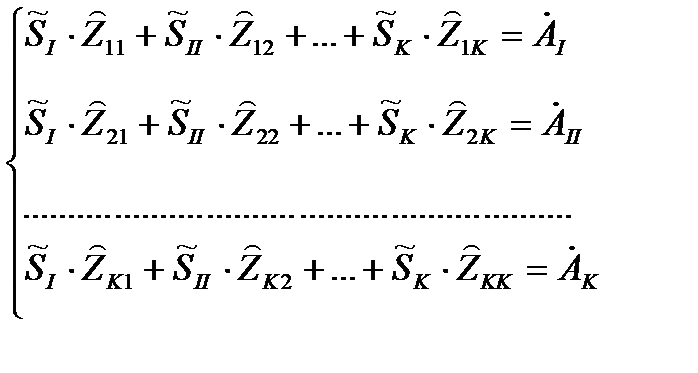 , (1.40)
, (1.40)
где 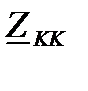 - собственное комплексное сопротивление К-го контура, равное сумме комплексных сопротивлений элементов входящих в контур;
- собственное комплексное сопротивление К-го контура, равное сумме комплексных сопротивлений элементов входящих в контур;
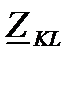 - общее комплексное сопротивление между контурами K и L, которое равно сумме комплексных сопротивление элементов находящихся в общих ветвях, которое берется со знаком плюс, если соответствующие контурные мощности имеют одинаковое направление в общих ветвях и со знаком минус, если направления контурных мощностей в этих ветвях взаимнопротивоположны;
- общее комплексное сопротивление между контурами K и L, которое равно сумме комплексных сопротивление элементов находящихся в общих ветвях, которое берется со знаком плюс, если соответствующие контурные мощности имеют одинаковое направление в общих ветвях и со знаком минус, если направления контурных мощностей в этих ветвях взаимнопротивоположны;
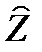 комплексное сопряженное значение сопротивления
комплексное сопряженное значение сопротивления 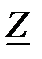 ;
;
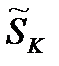 - комплексная мощность K-ого контура;
- комплексная мощность K-ого контура;
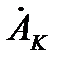 - свободный член K - контурного уравнения.
- свободный член K - контурного уравнения.
Правые части (свободные члены 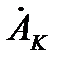 ) системы контурных уравнений формируются с использованием дерева схемы.
) системы контурных уравнений формируются с использованием дерева схемы.
Свободный член 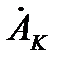 системы контурных уравнений для K-го уравнения равен алгебраической сумме произведений нагрузок узлов сети
системы контурных уравнений для K-го уравнения равен алгебраической сумме произведений нагрузок узлов сети 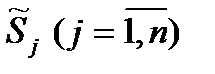 на сумму сопряженных сопротивлений только тех ветвей пути графа по дереву схемы от узла j до узла баланса (источника питания), которые принадлежат K-му контуру, и это произведение берется со знаком плюс, если путь графа совпадает с направлением контурной мощности и со знаком минус, если они не совпадают.
на сумму сопряженных сопротивлений только тех ветвей пути графа по дереву схемы от узла j до узла баланса (источника питания), которые принадлежат K-му контуру, и это произведение берется со знаком плюс, если путь графа совпадает с направлением контурной мощности и со знаком минус, если они не совпадают.
Пример 1.9.Сформировать систему контурных мощностей для схемы рассмотренной в примере 1.8.
С учетом допущений принятых в начале пп. 1.6.3.1 перейдем при формировании контурных уравнений от комплексных сопротивлений к длинам участков сети и от комплексных мощностей 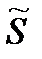 к активным мощностям
к активным мощностям 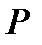 .
.
Cформируем граф сети, в котором ребра будут являться ветвями, а вершины узлами схемы сети.
Количество хорд всегда равно количеству контурных уравнений
kx = kк =m-(n-1) =5-(4-1)=2
Выберем в качестве хорд две внешние ветви (0-1 и 0-3, помеченные на рисунке 1.25 знаком ).
Тогда остальные ветви будут входить в дерево схемы.
| Р01 |
| Р03 |
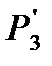
|
| Р1 |
| РI |
| РII |
| P2 |
Рисунок 1.25
Принимаем значение и направление мощностей в хордах соответствующим контурным мощностям, то есть PI=P01 и PII=P03;
Записываем систему контурных уравнений в формализованном виде
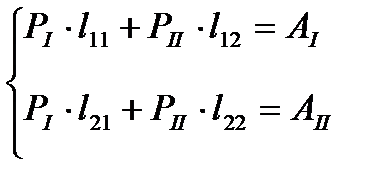 , (1.41)
, (1.41)
где 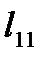 - собственная длина 1-го контура,
- собственная длина 1-го контура, 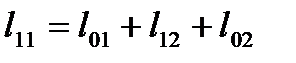 ;
;
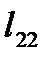 - собственная длина 2-го контура,
- собственная длина 2-го контура, 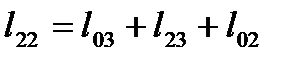 ;
;
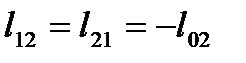
Для формирования 
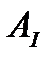 рассматриваем пути графа по дереву схемы от каждой нагрузки до источника питания (показаны на рисунке 1.26 штрих-пунктирными линиями).
рассматриваем пути графа по дереву схемы от каждой нагрузки до источника питания (показаны на рисунке 1.26 штрих-пунктирными линиями).
| Р01 |
| Р03 |
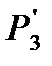
|
| Р1 |
| РI |
| РII |
| P2 |
Рисунок 1.26
Формируем 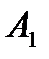
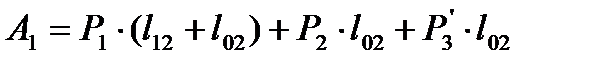 (1.42)
(1.42)
В этом выражении Р1 умножается на сумму длин 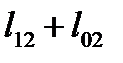 поскольку эти ветви входят в путь графа от узла 1 до узла 0 и принадлежат 1-му контуру и это произведение берется со знаком плюс, так как путь графа совпадает с направлением 1-ой контурной мощности. Аналогично нагрузка Р2 умножается на
поскольку эти ветви входят в путь графа от узла 1 до узла 0 и принадлежат 1-му контуру и это произведение берется со знаком плюс, так как путь графа совпадает с направлением 1-ой контурной мощности. Аналогично нагрузка Р2 умножается на 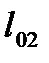 , а
, а 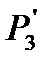 умножается только на
умножается только на 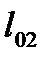 , хотя в путь графа от узла 3 до узла 0 входят ветви 3-2 и 0-2, но ветвь 3-2 не входит в рассматриваемый контур 1.
, хотя в путь графа от узла 3 до узла 0 входят ветви 3-2 и 0-2, но ветвь 3-2 не входит в рассматриваемый контур 1.
Аналогично формируем 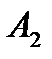
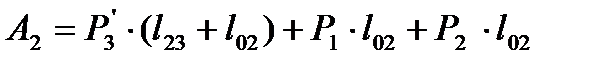 (1.43)
(1.43)
Таким образом, получим полную систему контурных уравнений
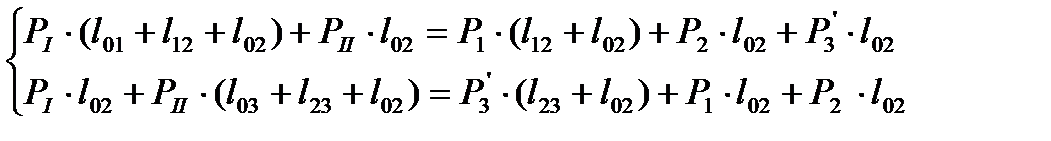 , (1.44)
, (1.44)
которая будет идентичной системе 1.39.
1.6.3.2 Аварийные режимы сложно-замкнутой сети
В качестве наиболее тяжелых послеаварийных режимов для сложно-замкнутой сети рассматриваются режимы с поочередным отключением головных участков.
| Р05 |
| Р03 |
| Р34 |
| Р12 |
| Р23 |
| Р02 |
| Р5 |
| Р4 |
| Р3 |
| Р1 |
| Р2 |
| Р01 |
| Р05 |
| Р03 |
| Р34 |
| Р12 |
| Р23 |
| Р5 |
| Р4 |
| Р3 |
| Р1 |
| Р2 |
Рисунок 1.28 - 2-ой аварийный режим (отключение участка 0-2)
| Р01 |
| Р05 |
| Р34 |
| Р12 |
| Р23 |
| Р02 |
| Р5 |
| Р4 |
| Р3 |
| Р1 |
| Р2 |
Рисунок 1.29 - 3-ий аварийный режим (отключение участка 0-3)
Для проверки проводов по току наиболее тяжелого после аварийного режима рассчитывается потокораспределение, а затем и токи для каждого из этих трех режимов и на каждом участке за аварийный ток принимается максимальный.
1.6.3.3.Проверка сложно замкнутого варианта сети по потери напряжения в нормальном режиме.
Проверка сложно замкнутого варианта сети по потери напряжения в нормальном режиме осуществляется до электрически наиболее удаленных точек сети, которыми являются точки потокораздела, или концевые точки радиально-магистральных участков, примыкающих к сложно замкнутой части сети (питающихся от узлов сложно замкнутой части сети). Если разомкнутый участок примыкает к узлы, являющимся точкой потокораздела, то проверку осуществляют только для конечной точки примыкающего разомкнутого участка.
Так для варианта сети изображенной на рисунке 1.19 электрически наиболее удаленной точкой сложно-замкнутого участка сети будет только точка 4 (точка 3 для данной сети является точкой потокораздела).
1.6.3.4.Проверка сложно замкнутого варианта сети по потери напряжения в послеаварийных режимах.
В послеаварийных режимах проверке подлежат все наиболее тяжелые послеаварийные режимы. Так для сети изображенной на рисунке 1.19 поочередно осуществляют проверку всех трех режимов (рисунки 1.27, 1.28, 1.29 на основе расчета потокораспределения для каждого из них).
Дата добавления: 2016-06-02; просмотров: 3160;
