Характеристик ожидаемой урожайности
Для построения методики определения статистических характеристик ОУ сделаем два предположения. Первое состоит в том, что если ДВУ данного года оказался ниже выбранного уровня ПрУ, то ОУ совпадает с фактическим уровнем ДВУ. Второе предположение постулирует, что если ДВУ данного года оказался выше ПрУ, то ОУ будет ниже ДВУ на некоторое значение, определяемое степенью лимитирования урожая агротехнологией, рассчитанной ранее на получение выбранного уровня ПрУ.
При сделанных предположениях ОУ может быть вычислен по формуле
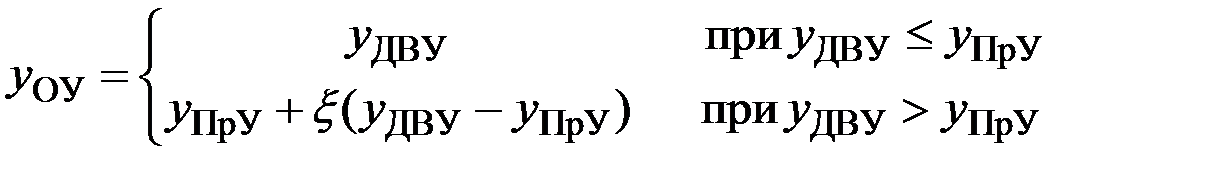
где ξ – коэффициент технологического лимитирования, лежащий между 0 и 1, при этом верхняя граница (ξ=1) соответствует отсутствию лимитирования, а нижняя (ξ=0), напротив – «жесткому» лимитированию, при котором получение урожая, больше планируемого, полагается невозможным.
Выражения для среднего значения и дисперсии ОУ при нормальном распределении значений ДВУ и фиксированном уровне ПрУ имеют вид:
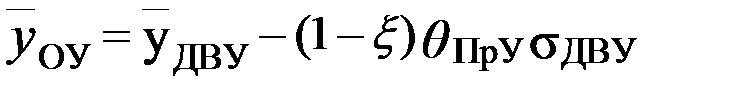 ;
;
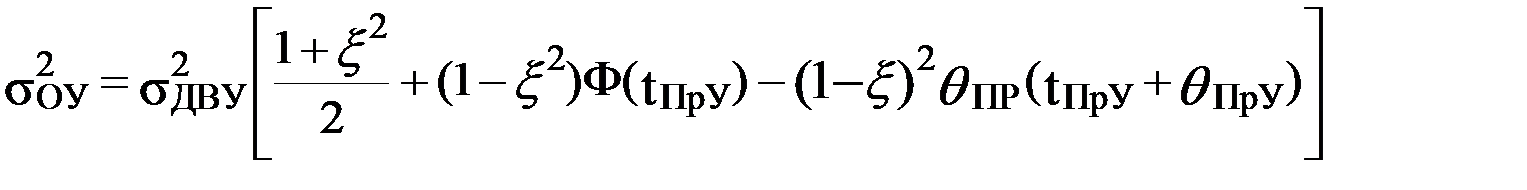 ,
,
где 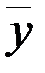 и σ – среднее значение и среднее квадратическое отклонение урожаев различных категорий соответственно.
и σ – среднее значение и среднее квадратическое отклонение урожаев различных категорий соответственно.
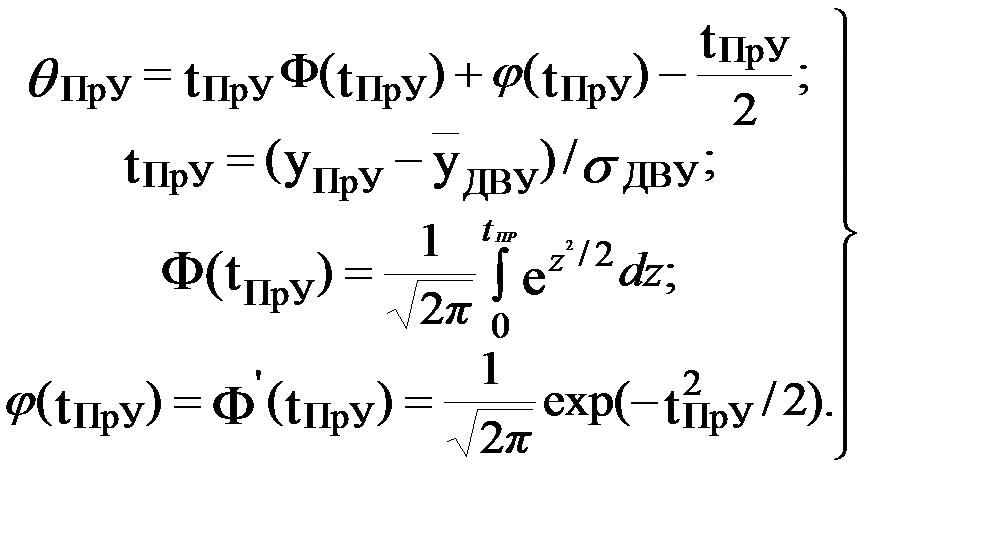
Легко понять, что 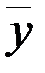 ОУ не может быть больше
ОУ не может быть больше 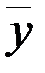 ДВУ, а σОУ всегда меньше σДВУ. Таким образом, лимитирующее влияние агротехнологий выражается как в уменьшении (по сравнению с
ДВУ, а σОУ всегда меньше σДВУ. Таким образом, лимитирующее влияние агротехнологий выражается как в уменьшении (по сравнению с 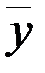 ДВУ) среднего значения ОУ, так и в снижении (по сравнению с σДВУ) его колебаний.
ДВУ) среднего значения ОУ, так и в снижении (по сравнению с σДВУ) его колебаний.
Приведем в качестве иллюстрации некоторые оценки, выполненные для случая когда ξ=0, что соответствует модели жесткого лимитирования. Для этого примера в таблице 8.70 даны значения параметров
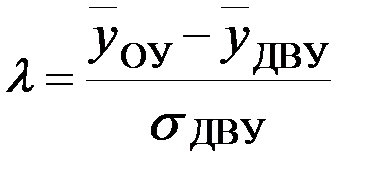 и
и 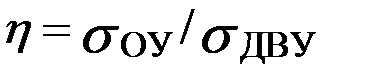 ,
,
рассчитанных при разных уровнях ПрУ (разные tПрУ)
8.70. Зависимость статистических характеристик ОУ
от уровня ПрУ при ξ=0
| tПрУ | -1,0 | -0,8 | -0,6 | -0,4 | -0,2 | 0,2 | 0,4 | 0,6 | 0,8 | |
| Λ | -1,08 | -0,92 | -0,77 | -0,63 | -0,51 | -0,40 | -0,31 | -0,23 | -0,17 | -0,12 |
| Η | 0,50 | 0,57 | 0,64 | 0,70 | 0,76 | 0,81 | 0,86 | 0,89 | 0,92 | 0,95 |
Как видно из таблицы 8.70, при достаточно высоких уровнях планируемых урожаев, когда tПрУ>1, величины 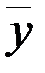 ОУ и σОУ практически совпадают с
ОУ и σОУ практически совпадают с 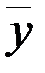 ДВУ и σДВУ. Снижение уровня планируемого урожая приводит к снижению
ДВУ и σДВУ. Снижение уровня планируемого урожая приводит к снижению 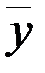 ОУ и σОУ. В частности, при планировании агротехнологий в расчете на средние многолетние условия, т.е. при ПрУ=
ОУ и σОУ. В частности, при планировании агротехнологий в расчете на средние многолетние условия, т.е. при ПрУ= 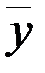 ДВУ, средний ожидаемый урожай будет ниже среднего многолетнего ДВУ на 0,4 σДВУ.
ДВУ, средний ожидаемый урожай будет ниже среднего многолетнего ДВУ на 0,4 σДВУ.
Отдельно следует рассмотреть вопрос о законе распределения yОУ. Это распределение отличается от нормального и для произвольных yПрУ и ξ записывается в виде
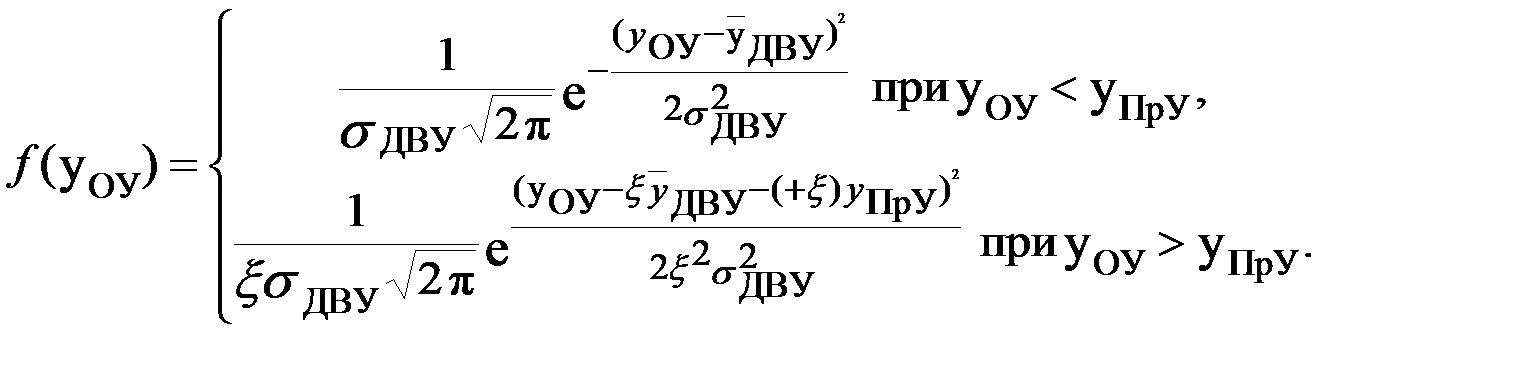
Выражение для статистической обеспеченности ожидаемых урожаев различных уровней:
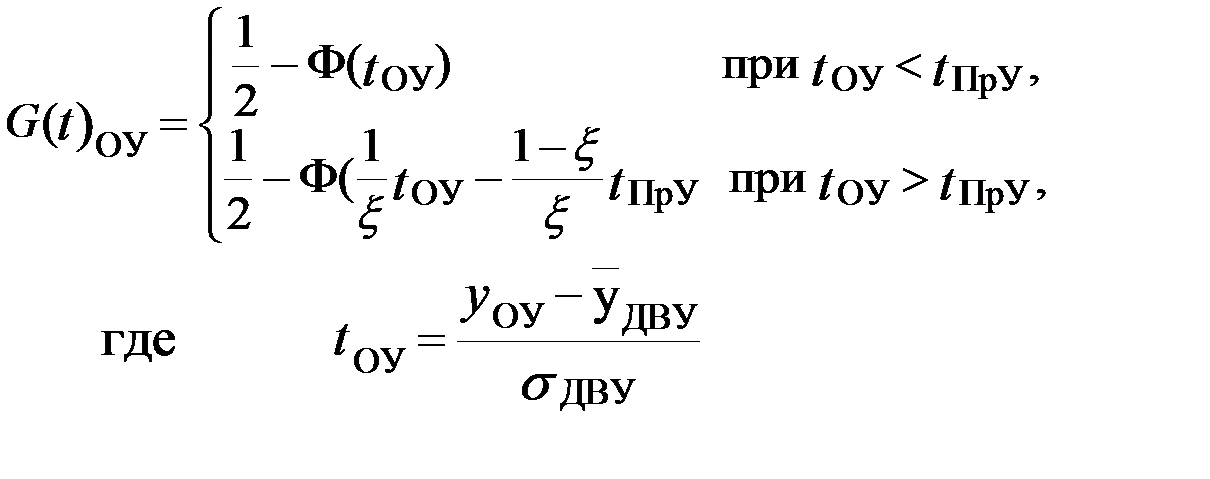
Статистическая обеспеченность G(tОУ) представляет собой вероятность того, что ожидаемый урожай yОУ будет не ниже выбранного уровня. Например, если принять ожидаемый урожай ОУ равным планируемому (ОУ=ПрУ) то следует, что вероятность получения урожаев не ниже планируемых может быть определена по формуле
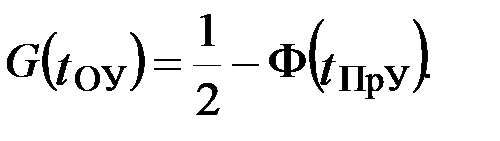
Изложенная выше методика устанавливает количественную взаимосвязь между уровнем планируемого урожая и статистическими характеристиками ожидаемого урожая. Однако вопрос о том, как, собственно, выбрать уровень планируемого урожая, остался пока открытым. Для его решения предлагается привлечь некоторые дополнительные соображения, позволяющие оценивать задание конкретного уровня планируемого урожая с хозяйственно-экономической точки зрения.
Обозначим через СУ стоимость единицы урожая возделываемой культуры, а через СТ и СТ(YПрУ) – технологические затраты, необходимые (следовательно и планируемые) для получения некоторого урожая YПрУ. Если в конкретном случае получен урожай Y, то чистый доход от его реализации может быть рассчитан как
u=CУY-CT(YПрУ)
Очевидно, что если величина Y была бы заранее известна, то каждый раз можно было бы выбрать такое YПрУ, которое обеспечивало бы получение максимум u. Однако, как уже отмечалось, вследствие изменчивости погодных условий при любом выборе YПрУ величина Y от случая к случаю будет меняться и, следовательно, оптимальность YПрУ следует понимать лишь в смысле получения наилучших средних статистических результатов. Исходя из этого, назовем климатологически оптимальной стратегией выбор такого уровня планируемого урожая, который обеспечивает достижение максимального среднего дохода 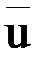 . Последний определяется как
. Последний определяется как
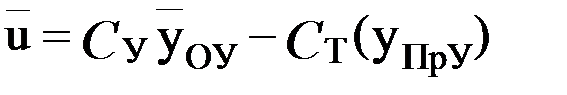 ,
,
и оптимум YПрУ отвечает выполнению равенства
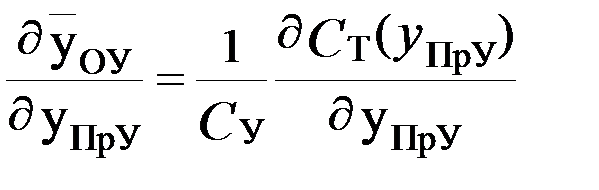
Конкретизируем последнюю зависимость в предположении, что технологические затраты увеличиваются пропорционально выбранному уровню YПрУ, т.е.
СТ(YПрУ)=a+bYПрУ
где a и b – некоторые коэффициенты.
Тогда для случая нормального распределения ДВУ получим
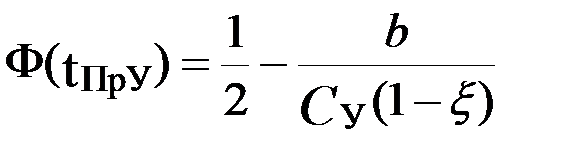 ,
,
где Φ – интеграл вероятности.
Проанализируем этот результат. Задача имеет решение когда
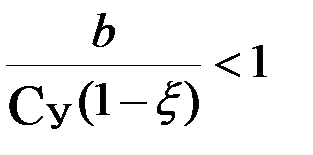 ,
,
причем для 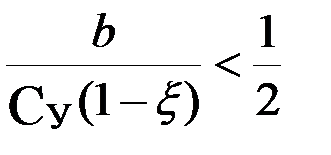 оптимальное значение tПрУ оказываетсяположительным, а для
оптимальное значение tПрУ оказываетсяположительным, а для 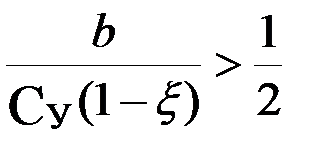 – отрицательным. В соответствии с этим оптимальной хозяйственной стратегией в первом случае является выбор уровня планируемого урожая, превосходящего
– отрицательным. В соответствии с этим оптимальной хозяйственной стратегией в первом случае является выбор уровня планируемого урожая, превосходящего 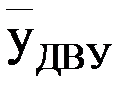 , а во втором – установление YПрУ, меньшего
, а во втором – установление YПрУ, меньшего 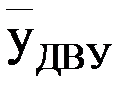 . Иначе говоря, при планировании агротехнических мероприятий на предстоящий сезон вегетации в первом случае целесообразно ориентироваться на условия более благоприятные, чем средние многолетние, а во втором случае, напротив, - на условия менее благоприятные, чем средние.
. Иначе говоря, при планировании агротехнических мероприятий на предстоящий сезон вегетации в первом случае целесообразно ориентироваться на условия более благоприятные, чем средние многолетние, а во втором случае, напротив, - на условия менее благоприятные, чем средние.
Для рассматриваемой линейной модели решение задачи отыскания оптимального уровня планируемого урожая может быть получено, исходя из других представлений. В частности, проанализируем к каким экономическим потерям Δu приводят отклонения фактического уровня ДВУ, соответствующего реально сложившимся погодным условиям, от заранее выбранного уровня YПрУ.
Если фактический ДВУ оказывается ниже YПрУ, то средства, которые затрачиваются на предполагаемое получение планируемого урожая, частично расходуются непроизводительно, поскольку урожаи выше ДВУ принципиально невозможны. Возникающие при этом потери составляют Δu=b(YПрУ-YДВУ). С другой стороны, если фактический ДВУ оказывается выше YПрУ, то вследствие лимитирующего влияния агротехнологии, ориентированной на более низкую продуктивность, часть потенциально возможного урожая Δy=(1-ξ)(YДВУ-YПрУ) теряется и возникающие убытки определяются величиной Δu=[CУ(1-ξ)-b](YДВУ-YПрУ). Объединение двух записанных равенств дает
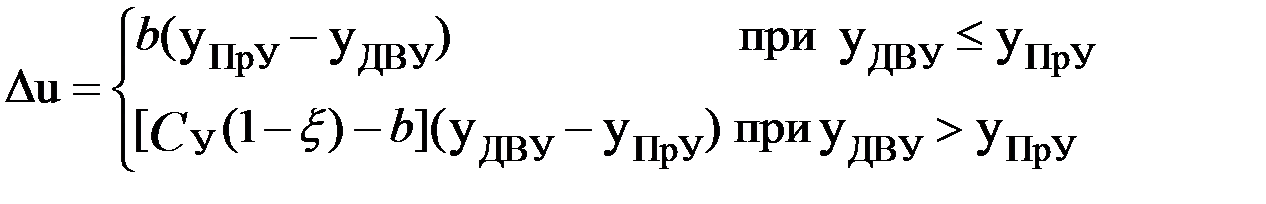
Очевидно, что при любом yПрУ=const величина Δu от случая к случаю будет меняться, в связи с чем, естественно, возникает вопрос: какой должна быть величина yПрУ, чтобы средние в статистическом смысле потери Δ 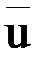 , обусловленные случайными колебаниями ДВУ, оказались минимальными.
, обусловленные случайными колебаниями ДВУ, оказались минимальными.
Оптимальный уровень планируемого урожая, при котором средние потери Δ 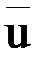 минимальны, находится из уравнения
минимальны, находится из уравнения
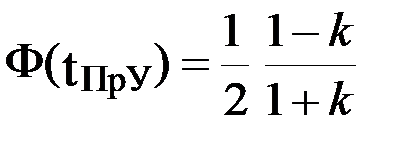 ,
,
где 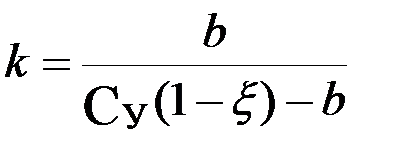 .
.
Численные значения оптимального tПрУ, обозначаемого через t0 приведены в таблице 8.71.
8.71. Оптимум tПрУ при разных k
| k | 1/20 | 1/10 | 1/5 | 1/3 | 1/2 | ||||||
| tПрУ | 1,67 | 1,34 | 0,97 | 0,63 | 0,43 | -0,43 | -0,67 | -0,97 | -1,34 | -1,67 |
Рассмотренная линейная модель, естественно не является универсальной. С ростом урожаев затраты на их получение возрастают не по линейному закону, а быстрее. Учитывая это, примем, например для СТ(YПрУ) квадратичную аппроксимацию вида
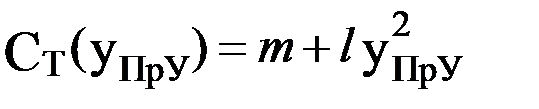 ,
,
где m и l – постоянные коэффициенты.
После несложных преобразований получим
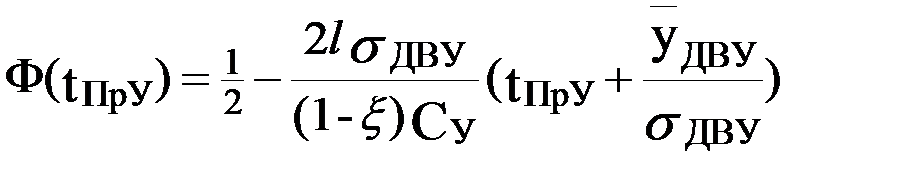 .
.
Легко убедиться, что это уравнение всегда имеет единственное решение, причем когда 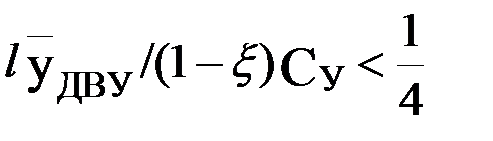 , величина t0 положительна, а при
, величина t0 положительна, а при 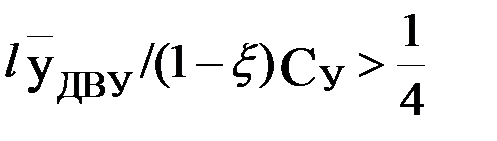 – отрицательна. В соответствии с этим уровень планируемого урожая в перовом случае целесообразно принять выше
– отрицательна. В соответствии с этим уровень планируемого урожая в перовом случае целесообразно принять выше 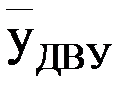 , а во втором – ниже его.
, а во втором – ниже его.
Разработка структурных моделей посевов сельскохозяйственных культур с учетом предшественников и планируемой урожайности при различных уровнях интенсификации агротехнологий
Для поэтапного (по элементам продуктивности) формирования запланированного уровня урожайности той или иной культуры сначала нужно составить модель ее посева (соотношение элементов продуктивности), реализация которой (с неизбежной корректировкой в процессе вегетации) обеспечит достижение плановой урожайности.
Полностью реализовать запрограммированную модель посева (урожая), разумеется, вряд ли возможно, поскольку каждый из элементов урожайности очень сильно варьирует в зависимости от постоянно меняющихся условий жизни растений. Тем не менее такие модели имеют важное значение для определения оптимальных норм высева семян (коэффициента высева), а также для управления формированием каждого последующего элемента урожайности, исходя из уровня развития предыдущих элементов.
Урожайность – произведение двух сомножителей – числа растений (или колосьев) на единице площади и средней продуктивности одного растения (или колоса). Причем величины этих основных элементов урожайности, в свою очередь, представляют собой произведение других сомножителей, величины которых очень сильно колеблются в зависимости от условий и, как правило, находятся друг с другом во взаимокомпенсационной зависимости. Например, с увеличением числа растений на площади уменьшается их кустистость и выживаемость, снижается средняя продуктивность растений и т. п. Эта связь выражена формулой М.Т. Савицкого:
У = Р × З × А : 10000 ,
где У – урожайность зерновой культуры, ц/га; Р – число продуктивных колосьев (метелок) к уборке, шт./м2; З – число зерен в колосе (метелке); А – масса 1000 зерен при стандартной влажности, г.
Число продуктивных колосьев (метелок) к уборке (Р) пропорционально числу высеянных на той же площади зерен (М – в млн. шт./га), хозгодности семян (Х, %), полевой всхожести семян (П, %), выживаемости растений к уборке (В, %) и продуктивной кустистости (К):
Р = М × Х × П × В : 10000
Подставив значение Р в предыдущую формулу, получим:
У = М × Х × П × В × К × З × А : 108,
Для зернобобовых и капустных культур:
У = М × Х × П × В × Б × С × А : 108,
где Б – среднее число бобов (стручков) на растении; С – число семян в 1 бобе (стручке). Остальные обозначения те же, что и в предыдущей формуле.
На основании этой формулы, зная уровень запланированной урожайности, можно определить значение любого из сомножителей. Эта формула позволяет рассчитать структурную модель посева, используя при этом реальные (варьирующие в допустимых пределах) элементы урожайности. Число зерен или семян на растении зависит от продуктивной кустистости растения (К) и числа зерен в 1 соцветии (Ч):
З = К × Ч – у зерновых культур;
З = Б × С – у зернобобовых и капустных культур.
Для клубнеплодных культур:
У = Р × Кл × М : 106,
где Р – число растений (кустов) к уборке, шт./м2; Кл – число клубней на 1 растении (кусте), штук; М – средняя масса 1 клубня, г.
Для корнеплодных, бахчевых, кормовых культур:
У = Р × М :10,
где Р – число растений к уборке, шт./м2; М – средняя масса одного корнеплода (растения), г.
Абсолютно точно предвидеть ход формирования каждого элемента урожайности по мере вегетации посева нельзя. Но, ведя учет элементов урожайности в процессе роста (органогенеза) растений и сверяя с запрограммированной моделью, можно в определенной мере регулировать процесс органогенеза (формирование элементов урожайности). Аналогичные модели следует составлять для всех культур (таблицы 8.73.-8.77).
Дата добавления: 2016-05-05; просмотров: 912;
