Средняя ошибка репрезентативности
| № п/п | Вид выборки | Тип отбора | |
| повторный отбор | бесповторный отбор | ||
| 1. | Собственно-случайная выборка | 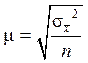
| 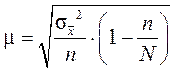
|
| 2. | Механическая выборка | - | 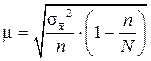
|
| 3. | Типическая выборка: - при отборе, пропорциональном объему типических групп - при отборе, пропорциональном дифференциации признака |
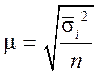
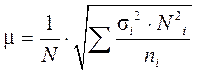
|
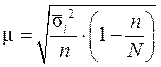
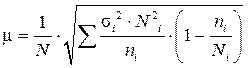
|
| 4. | Серийная выборка | 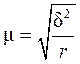
| 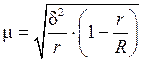
|
| 5. | Малая выборка | - | 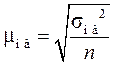 ,
причем ,
причем 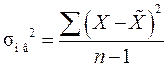
|
Средняя ошибка выборки можно представить как 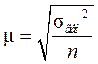 , причем
, причем 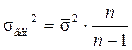 . Предельная ошибка выборки
. Предельная ошибка выборки 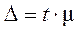 , где
, где 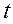 - коэффициент доверия, вычисляемый по таблице в зависимости от вероятности. Согласно теореме А.М. Ляпунова, вероятность той или иной величины предельной ошибки, при достаточно большом объеме выборочной совокупности, подчиняется нормальному закону распределения и может быть определена на основе интеграла Лапласа:
- коэффициент доверия, вычисляемый по таблице в зависимости от вероятности. Согласно теореме А.М. Ляпунова, вероятность той или иной величины предельной ошибки, при достаточно большом объеме выборочной совокупности, подчиняется нормальному закону распределения и может быть определена на основе интеграла Лапласа:
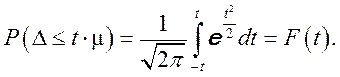
Значения интеграла Лапласа при различных 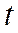 приведены в таблице:
приведены в таблице:
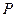
| 0,683 | 0,950 | 0,954 | 0,997 |
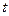
| 1,96 |
Выборочное наблюдение проводится в целях распространения выводов, полученных по данным выборки, на генеральную совокупность. Одной из основных задач является оценка по данным выборки исследуемых характеристик (параметров) генеральной совокупности.
Предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы:
- для среднего размера количественного признака:
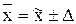 или
или 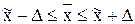 ;
;
- для доли качественного признака:
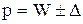 или
или 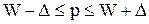 .
.
Это означает, что с заданной доверительной вероятностью можно утверждать, что значения генеральной средней следует ожидать в пределах от 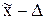 до
до 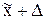 , а значения генеральной доли – в пределах от
, а значения генеральной доли – в пределах от 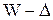 до
до 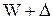 .
.
Наряду с абсолютным значением предельной ошибки выборки рассчитывается и предельная относительная ошибка выборки, которая представляет процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности:
- для среднего размера количественного признака: 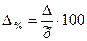 ;
;
- для доли качественного признака: 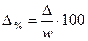 .
.
Дата добавления: 2016-05-25; просмотров: 458;
