Трубопроводы с насосной подачей жидкостей

Как уже отмечалось выше, перепад уровней энергии, за счет которого жидкость течет по трубопроводу, может создаваться работой насоса, что широко применяется в машиностроении. Рассмотрим совместную работу трубопровода с насосом и принцип расчета трубопровода с насосной подачей жидкости.

Трубопровод с насосной подачей жидкости может быть разомкнутым, т.е. по которому жидкость перекачивается из одной емкости в другую (рисунок 6.8, а), или замкнутым (кольцевым), в котором циркулирует одно и то же количество жидкости (рисунок 6.8, б).

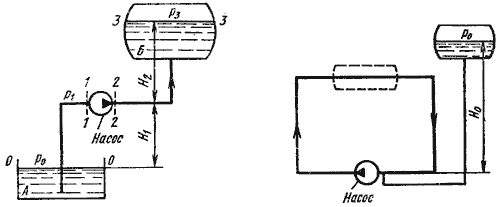
Рисунок 6.8 – Трубопроводы с насосной подачей

Рассмотрим трубопровод, по которому перекачивают жидкость из нижнего резервуара с давлением P ₀ в другой резервуар с давлением P₃ (рисунок 6.8, а). Высота расположения оси насоса H₁ называется геометрической высотой всасывания, а трубопровод, по которому жидкость поступает к насосу, всасывающим трубопроводом или линией всасывания. Высота расположения конечного сечения трубопровода H₂ называется геометрической высотой нагнетания, а трубопровод, по которому жидкость движется от насоса, напорным или линией нагнетания.

Составим уравнением Бернулли для потока рабочей жидкости во всасывающем трубопроводе, т.е. для сечений 0-0 и 1-1 (принимая α = 1):

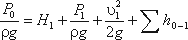
Это уравнение является основным для расчета всасывающих трубопроводов.

Теперь рассмотрим напорный трубопровод, для которого запишем уравнение Бернулли, т.е. для сечений 2-2 и 3-3:

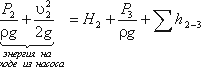
Левая часть этого уравнения представляет собой энергию жидкости на выходе из насоса. А на входе насоса энергию жидкости можно будет аналогично выразить из уравнения:

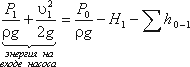
Таким образом, можно подсчитать приращение энергии жидкости, проходящей через насос. Эта энергия сообщается жидкости насосом и поэтому обозначается обычно H_нас.

Для нахождения напора H_нас вычислим уравнение :

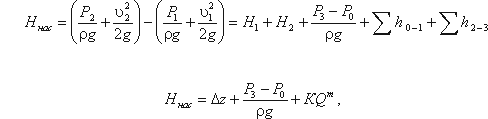
где Δz - полная геометрическая высота подъема жидкости, Δz = H ₁ + H₂;
КQ^m - сумма гидравлических потерь,
P₃ и Р₀ - давление в верхней и нижней емкости соответственно.

Если к действительной разности уровней Δz добавить разность пьезометрических высот ( P₃ - Р₀ ) ( ρg ), то можно рассматривать увеличенную разность уровней

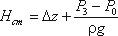
и формулу можно переписать так:

H_нас = H_ст + KQ^m

Из этой формулы делаем вывод, что

H_нас = H_потр

Отсюда вытекает следующее правило устойчивой работы насоса: при установившемся течении жидкости в трубопроводе насос развивает напор, равный потребному.

На этом равенстве основывается метод расчета трубопроводов с насосной подачей, который заключается в совместном построении в одном и том же масштабе и на одном графике двух кривых: напора H_потр = f₁(Q) и характеристики насоса H_нас = f₂(Q) и в нахождении их точки пересечения (рисунок 6.9).

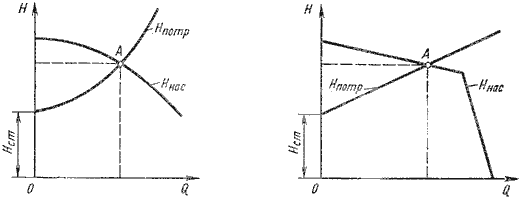
Рисунок 6.9 – Графическое нахождение рабочей точки

Характеристикой насоса называется зависимость напора, создаваемого насосом, от его подачи (расхода жидкости) при постоянной частоте вращения вала насоса. На рисунок 6.9 дано два варианта графика: а - для турбулентного режима; б - для ламинарного режима. Точка пересечения кривой потребного напора с характеристикой насоса называется рабочей точкой. Чтобы получить другую рабочую точку, необходимо изменить открытие регулировочного крана (изменить характеристику трубопровода) или изменить частоту вращения вала насоса.