Подходы к измерению информации
Общая схема передачи сообщения
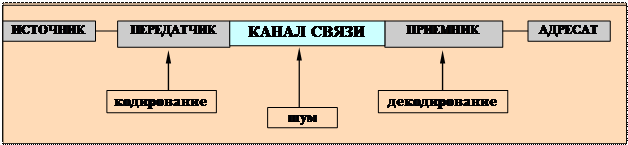
Источник сообщения - человек или физический, технический и т.д. процесс. Сообщение может быть закодировано (шифр, преобразование человеческой речи в радио-сигнал, электромагнитные колебания, оптические сигналы и т.д.).
Ø От передатчика до приемника закодированный сигнал передается по каналу связи. В качестве носителя при передаче сообщения по каналу связи чаще всего используют:
w механические движения (механика)
w механическое давление жидкости или газа (гидравлика, пневматика)
w волны давления в жидкостях, газах, твердом теле (акустика)
w электрические токи и напряжения,
w электромагнитные волны (радио, свет).
Пропускная способность канала – количество передаваемой по каналу информации, измеряется в бит/с.
2.6. Измерения информации
Подходы к измерению информации
В информатике используются различные подходы к измерению информации:
Алфавитный (кибернетический, объемный) подход к измерению информациине связывает кол-во информации с содержанием сообщения. Кол-во информации зависит от объема текста и мощности алфавита.
Алфавит – конечное множество различных знаков, символов, для которых определена операция конкатенации (приписывания, присоединения символа к символу или цепочке символов); с ее помощью по определенным правилам соединения символов и слов можно получать слова (цепочки знаков) и словосочетания (цепочки слов) в этом алфавите.
Конечная последовательность букв алфавита называется словом.
Длиной некоторого слова называется число составляющих его символов.
N при алфавитном подходе называют мощностью алфавита. Информационная ёмкость каждого знака зависит от количества знаков в алфавите. Следовательно, каждый из N символов несёт i бит информации.
2i = N
Остаётся подсчитать количество символов в тексте сообщения k.
Количество информации:
I = k × i
Алфавитный подход является объективным способом измерения информации и подходит для работы технических устройств.
Минимальная мощность алфавита, пригодного для передачи информации, равна 2. Такой алфавит называется двоичным алфавитом. Информационный вес символа в двоичном алфавите легко определить. Поскольку 2i = 2, то i = 1 бит. Итак, один символ двоичного алфавита несет 1 бит информации.
Например, основная физическая единица длины — метр. Но существуют миллиметр, сантиметр, километр. Расстояния разного размера удобно выражать через разные единицы. Так же обстоит дело и с измерением информации.
1 бит — это исходная единица.
Следующая по величине единица — байт. Байт вводится как информационный вес символа из алфавита мощностью 256. Поскольку 256 = 28, то 1 байт = 8 бит.
Ограничений на max мощность алфавита нет, но есть достаточный алфавит мощностью 256 символов. Этот алфавит используется для представления текстов в компьютере. Поскольку 256=28, то 1 символ несет в тексте 8 бит информации.
Пример: слово «мир» несет 24 бит информации.
Содержательный (энтропийный, вероятностный) подход к измерению информации. Этотподход основан на том, что факт получения информации всегда связан с уменьшением неопределенности (энтропии) системы. Сообщение несет информацию для человека, если содержащиеся в нем сведения являются для него новыми и понятными. Если сообщение не информативно, то количество информации с точки зрения человека = 0.
Пример: вузовский учебник по высшей математике содержит знания, но они не доступны 1-класснику.
Количество информации - это мера уменьшения неопределенности. В качестве меры неопределенности вводится энтропия Н, а количество информации равно:
I = Hapr – Haps
гдеHapr – априорная энтропия о состоянии исследуемой системы или процесса;
Haps – апостериорная энтропия.
Апостериори (от лат. aposteriori – из последующего) – происходящее из опыта (испытания, измерения). Априори (от лат. apriori – из предшествующего) – понятие, характеризующее знание, предшествующее опыту (испытанию) и независимое от него.
В случае, когда в ходе испытания имевшаяся неопределенность снята (получен конкретный результат, то есть Haps = 0), количество полученной информации совпадает с первоначальной энтропией.
Так, американский инженер Р. Хартли (1928 г.) процесс получения информации рассматривает как выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определяет как двоичный логарифм N.
| Формула Хартли: H= log2N. |
Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: I = log2100 » 6,644. То есть сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единиц информации.
Приведем другие примеры равновероятных сообщений:
1. при бросании монеты: "выпала решка", "выпал орел";
2. на странице книги: "количество букв чётное", "количество букв нечётное".
Определим теперь, являются ли равновероятными сообщения "первой выйдет из дверей здания женщина" и "первым выйдет из дверей здания мужчина". Однозначно ответить на этот вопрос нельзя. Все зависит от того, о каком именно здании идет речь. Если это, например, станция метро, то вероятность выйти из дверей первым одинакова для мужчины и женщины, а если это военная казарма, то для мужчины эта вероятность значительно выше, чем для женщины.
Для задач такого рода американский учёный Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе.
| Формула Шеннона: I = – ( p1 log2 p1 + p2 log2 p2 + . . . + pN log2 pN ), где pi — вероятность того, что именно i-е сообщение выделено в наборе из N сообщений. N – количество сообщений |
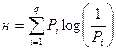 |
Легко заметить, что если вероятности p1, ..., pN равны, то каждая из них равна 1/N, и формула Шеннона превращается в формулу Хартли.
Задача1: Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика, если в непрозрачном мешочке находится 50 белых, 25красных, 25 синих шариков
1) всего шаров 50+25+25=100
2) вероятности шаров 50/100=1/2, 25/100=1/4, 25/100=1/4
3)I= -(1/2 log21/2 + 1/4 log21/4 + 1/4 log21/4) = -(1/2(0-1) +1/4(0-2) +1/4(0-2)) = 1,5 бит
Количество информации достигает max значения, если события равновероятны, поэтому количество информации можно расcчитать по формуле
Задача2 : В корзине лежит 16 шаров разного цвета. Сколько информации несет сообщение, что достали белый шар?
т.к. N = 16 шаров, то I = log2 N = log2 16 = 4 бит.
Алгоритмическое измерение информации [2]
Был предложен в 1965 году академиком А.Н. Колмогоровым. Алгоритмическая сложность некоторой последовательности данных определяется как минимальная длина вычислительного алгоритма, который мог бы воспроизвести заданную последовательность.
Например: слово 000000 – простое, слово 01010101 – более сложное, а слово, в котором 0 и 1 выбираются экспериментально при бросании монеты (1 – орел, 0 – решка), еще сложнее.
Компьютерная программа, печатающая первое слово, совсем простая; для получение второго слова нужна более сложная программа, которая будет печатать символ, противоположный предыдущему. Случайная последовательность, не обладающая никакими закономерностями, может быть напечатана программой, в которой каждый очередной символ будет печататься отдельным оператором. То есть длина такой программы будет близка к длине самой последовательности. Следовательно, любому сообщению можно приписать количественную характеристику, отражающую размер программы, которая позволяет ее воспроизвести.
| <== предыдущая лекция | | | следующая лекция ==> |
| Плавники выполняют разные функции. | | | Графические форматы. Аппаратное обеспечение компьютерной графики |
Дата добавления: 2016-05-25; просмотров: 22846;
