Естественный и поляризованный свет.
Лекция 4. Поляризация и дисперсия света
План лекции
4.1. Естественный и поляризованный свет.
4.2. Поляризация при отражении и преломлении света. Закон Брюстера.
4.3. Двойное лучепреломление. Поляроиды и поляризационные призмы.
4.4. Вращение плоскости поляризации.
4.5. Дисперсия света. Области нормальной и аномальной дисперсии.
Естественный и поляризованный свет.
Несмотря на то, что световые волны поперечны, они обычно не обнаруживают асимметрии относительно луча. Это обусловлено тем, что в естественном свете,
испускаемом обычными источниками, имеются колебания, совершающиеся в самых различных направлениях, перпендикулярных к лучу (см. рис. 4.1). Эти колебания быстро и беспорядочно сменяют друг друга.
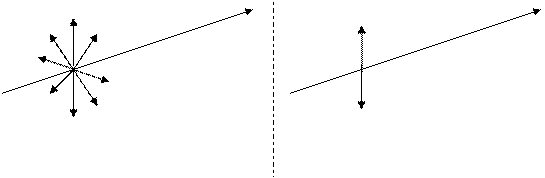 |
| Луч | Луч |
| Естественный свет | Линейно-поляризованный свет |
Рис. 4.1
Свет, в котором направления колебаний вектора электрического поля 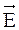 упорядочены каким либо образом, называется поляризованным(рис. 4.1).
упорядочены каким либо образом, называется поляризованным(рис. 4.1).
Если вектор 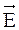 поворачивается вокруг луча, одновременно периодически изменяясь по величине, то свет называется эллиптически-поляризованным. Если конец вектора
поворачивается вокруг луча, одновременно периодически изменяясь по величине, то свет называется эллиптически-поляризованным. Если конец вектора 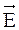 , поворачиваясь вокруг луча, описывает окружность, свет называется поляризованным по кругу.
, поворачиваясь вокруг луча, описывает окружность, свет называется поляризованным по кругу.
Плоскость, в которой колеблется световой вектор в плоскополяризованной волне, называется плоскостью колебаний.
Рассмотрим два взаимно перпендикулярных колебания, совершающихся вдоль осей x и y и отличающихся по амплитуде и фазе (рис. 4.2):
Ех = Е1cos wt, Еy = Е2 cos (wt+j).
 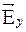 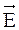
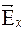
| y
EE 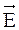 x
x
|
Рис. 4.2
Результирующая напряженность 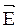 является векторной суммой напряженностей
является векторной суммой напряженностей 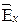 и
и 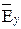 . Угол a между направлениями векторов
. Угол a между направлениями векторов 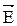 и
и 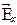 определяется выражением:
определяется выражением:
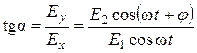 .
.
Если разность фаз j претерпевает случайные хаотические изменения, то и угол a, т. е. направление светового вектора 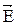 будет испытывать скачкообразные неупорядоченные изменения. В соответствии с этим естественный свет можно представить как наложение двух некогерентных электромагнитных волн, поляризованных во взаимно перпендикулярных плоскостях и имеющих одинаковую интенсивность.
будет испытывать скачкообразные неупорядоченные изменения. В соответствии с этим естественный свет можно представить как наложение двух некогерентных электромагнитных волн, поляризованных во взаимно перпендикулярных плоскостях и имеющих одинаковую интенсивность.
Две когерентные плоскополяризованные световые волны, плоскости колебаний которых перпендикулярны, при наложении друг на друга дают эллиптически поляризованную волну. При разности фаз j, равной нулю или p, эллипс вырождается в прямую линию и получается плоскополяризованный свет. При j = ±p/2 и равенстве амплитуд складываемых световых волн эллипс превращается в окружность – получается свет, поляризованный по кругу.
Плоскополяризованный свет можно получить из естественного с помощью устройств, называемых поляризаторами. Эти устройства свободно пропускают колебания, параллельные плоскости, называемой плоскостью поляризатора, и полностью или частично задерживают колебания, перпендикулярные к его плоскости. При частичной задержке на выходе из несовершенного поляризатора получается свет, в котором колебания одного направления преобладают над колебаниями других направлений. Такой свет называется частично поляризованным. Его, как и естественный свет, можно представить в виде наложения двух некогерентных плоскополяризованных волн с взаимно перпендикулярными плоскостями колебаний. Отличие заключается в том, что в случае естественного света амплитуда двух колебаний одинакова, а в случае частично поляризованного – разная.
Степенью поляризации называется отношение: 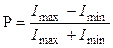 .
.
Здесь Iminи Imax- соответственно, минимальное и максимальное значения интенсивности прошедшего через совершенный поляризатор частично поляризованного света. Для плоскополяризованного света Imin = 0 и P = 1; для естественного света Imin= Imaxи P = 0.
Колебание амплитуды светового вектора Е, совершающееся в плоскости, образующей с плоскостью поляризатора угол a, можно разложить на два колебания с амплитудами (см. рис. 4.3):
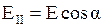 и
и 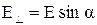 .
.
В естественном свете все значения угла a, под которыми происходят колебания светового вектора, равновероятны, поэтому доля света, прошедшего через поляризатор, будет пропорциональна среднему значению cos2a, то есть ½. При этом интенсивность прошедшего через поляризатор естественного света равна:
I0 = 1/2×Iест
Первое колебание пройдет через поляризатор, второе будет задержано. Интенсивность прошедшей волны пропорциональна
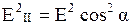 ,
то есть равна I0 cos2 a, где I0 – интенсивность колебаний с амплитудой Е.
Следовательно, интенсивность I прошедшего ,
то есть равна I0 cos2 a, где I0 – интенсивность колебаний с амплитудой Е.
Следовательно, интенсивность I прошедшего
| плоскость
 поляризации
Е
ЕII
Е^
Рис. 4.3 поляризации
Е
ЕII
Е^
Рис. 4.3
|
через поляризатор (анализатор) поляризованного света I0 определяется выражением
I = I0 cos2 a.
Это соотношение носит название закона Малюса1.
Если на пути естественного света поставить два поляризатора, плоскости которых образуют угол a, то, согласно закону Малюса, интенсивность прошедшего через них света равна:
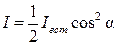 .
.
Если коэффициент пропускания поляризаторов t не равен 1, то интенсивность света, прошедшего через каждый поляризатор, пропорциональна t, то есть

1Э. Малюс (1775 – 1812), французский физик.
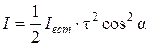 .
.
4.2. Поляризация при отражении и преломлении света. Закон Брюстера.
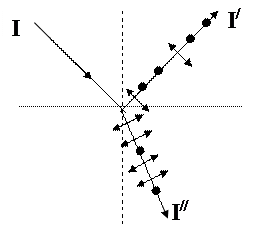
Если угол падения света на границу раздела двух диэлектриков (например, на поверхность стеклянной пластинки) отличен от нуля, отраженный и преломленный лучи оказываются частично поляризованными (рис. 4.4). В отраженном свете преобладают колебания, перпендикулярные плоскости падения (обозначены точками), а в преломленном луче – колебания, параллельные плоскости падения (обозначены стрелками).
|
Рис. 4.4
Степень поляризации зависит от угла падения. При угле падения, удовлетворяющем условию
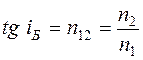 , (4.1)
, (4.1)
отраженный луч полностью поляризован (линейно-поляризованный). Степень поляризации преломленного луча достигает при этом наибольшего значения, но луч остается частично поляризованным. Соотношение (4.1) носит название закона Брюстера1, а угол iБ – угол Брюстера.
Дата добавления: 2016-04-22; просмотров: 2170;
