ТЕПЛОВЫЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ

Как известно, все тела при нагревании расширяются. Чтобы объяснить природу теплового расширения твердых тел, надо рассмотреть зависимость энергии взаимодействия частиц от расстояния между ними (см. введение по теме: "Молекулярные силы").

Если бы частицы были совершенно неподвижны, т.е. если бы их кинетическая энергия равнялась нулю, то они находились бы друг от друга на расстоянии r₀, соответствующем дну потенциальной ямы (рис. 1). Но в действительности частицы, находящиеся в узлах кристаллической решётки тела, не находятся в состоянии покоя, а участвуют в тепловой колебательном движении около положения равновесия. Рассмотрим колебания частицы 2 в системе координат, связанной с частицей 1. Вид колебаний будет определяться формой потенциальной кривой, изображенной на рис. 1.

При повышении температуры увеличивается полная энергия частицы, и соответственно возрастает амплитуда колебаний. В момент прохождения частицей положения равновесия ее кинетическая энергия принимает максимальное значение, пусть это значение равно W . Потенциальная энергия частицы в этот момент равна –U₀(рис. 1.). При движении частицы в сторону сближения с частицей 1 энергия расходуется на преодоление сил отталкивания и переходит в потенциальную энергию взаимодействия. Потенциальная энергия увеличивается на ΔU₀ = W и становится равной – (U₀ – ΔU)при этом частица смещается относительно положения равновесия на Δr₁. При движении частицы в другую сторону ее кинетическая энергия будет расходоваться на преодоление сил притяжения и также превращаться в потенциальную. При этом оказывается, что частица 2 смещается вправо на расстояние Δr₂, большее, чем Δr₁, как видно из рисунка. Таким образом, колебания частиц в решетке являются ангармоничными. Эта ангармоничность связана с асимметрией потенциальной кривой относительно прямой bd (ее левая ветвь ab идет значительно круче, чем правая ветвь bc). В свою очередь, эта асимметрия определяется характером зависимости от расстояния сил взаимодействия между парами частиц, тем, что сила отталкивания убывает с расстоянием быстрее, чем сила притяжения.

Если бы частица 2 совершала чисто гармонические колебания, изменение ее потенциальной энергии описывалось бы при этом параболой, и отклонения от положения равновесия OA₁ и OA₂ были бы равны. В этом случае нагревание не могло бы вызвать расширения тела, так как с увеличением температуры возрастала бы только амплитуда колебаний, а средние положения частиц оставались бы неизменными.

В реальном случае в результате асимметрии потенциальной кривой при Т > 0 К среднее положение частицы (точка O₁ на рис. 1) уже не совпадает с положением равновесия O, а смещено вправо на расстояние Δ = (Δr₂ - Δr₁). Это означает увеличение среднего расстояния между частицами на величину Δ.Чем выше температура, тем величина Δбольше. Поэтому при нагревании среднее расстояние между частицами увеличивается и, следовательно, тело будет расширяться.

Количественно тепловое расширение твердых тел характеризуется коэффициентом линейного расширения, определяемым соотношением

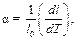
(1)

где l₀- длина тела при начальной температуре. Коэффициент линейного расширения характеризует относительное изменение длины твердых тел при изменении их температуры на один градус.

Потенциальную энергию взаимодействия атомов при смещении на расстояние Δr от положения равновесия в решетке при T = 0 К можно приближенно записать в виде

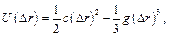
(2)

где член с (Δr)³ описывает асимметрию взаимного отталкивания атомов, с - коэффициент «меткости, определяющий частоту гармонических колебаний, g - коэффициент ангармоничности.

В случае малых смещений (энергия, связанная с ангармоничностью, мала) расчет показывает, что при нагревании тела до температуры Т среднее расстояние между частицами увеличивается на величину ,равную

(3)

Относительное линейное расширение тела, представляющее собой отношение изменения среднего расстояния между частицами к расстоянию между ними r₀равно

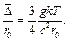
(4)

Оно оказывается пропорциональным абсолютной температуре тела. Коэффициент пропорциональности

(5)

представляет собой коэффициент линейного расширения тела.

Опыт подтверждает, что при достаточно высоких температурах расширение тела пропорционально абсолютной температуре, и α не зависит от температуры. Однако в области низких температур α ведет себя так же, как и теплоемкость твердого тела С_v:уменьшается с уменьшением Т и при К согласно третьему закону термодинамики.

То, что тепловое расширение и теплоемкость связаны друг с другом, следует из того факта, что α и C_vсвязаны с колебаниями решетки. Теплоемкость тела связана с увеличением средней энергии тепловых колебаний атомов, зависящей от амплитуды колебаний: α непосредственно связан со средними расстояниями между атомами, которые тоже зависят от амплитуды колебаний. Отсюда следует важный закон, открытый Грюнейзеном. Отношение α к C_v твердого тела для данного вещества есть величина постоянная (т.е. не зависящая от температуры).