Підсилювачі на польових транзисторах
2.1. Схеми та режими
Режими та схеми увімкнення польових транзисторів у підсилювальних каскадах залежать від їх конкретних різновидів.
|
|
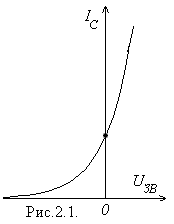
МДН - транзистор з вбудованим каналом 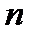 - каналом має прохідну характеристику подібну до зображеної на рис.2.1. Робоча точка може бути встановлена при
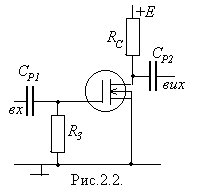
- каналом має прохідну характеристику подібну до зображеної на рис.2.1. Робоча точка може бути встановлена при 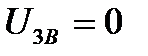 і. отже, потреби в подачі зміщення на затвор не буде. Схема увімкнення такого транзистора наведена на рис.2.2.
і. отже, потреби в подачі зміщення на затвор не буде. Схема увімкнення такого транзистора наведена на рис.2.2.
Розділовими ємностями 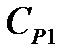 та
та 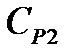 каскад «відгороджено» від пристроїв, які підключаються до його входу і виходу. Ці ємності вільно пропускають підсилюваний змінний сигнал, але не допускають впливу зовнішніх пристроїв на режим роботи транзистора. Резистор
каскад «відгороджено» від пристроїв, які підключаються до його входу і виходу. Ці ємності вільно пропускають підсилюваний змінний сигнал, але не допускають впливу зовнішніх пристроїв на режим роботи транзистора. Резистор 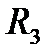 забезпечує виконання умови
забезпечує виконання умови 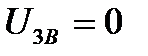 : через нього малі струми затвору стікають на землю, не створюючи скільки-небудь помітного спаду напруги на цьому опорі. Але якби опору
: через нього малі струми затвору стікають на землю, не створюючи скільки-небудь помітного спаду напруги на цьому опорі. Але якби опору 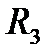 не було, то постійний потенціал затвору визначався б струмами затвору та ізоляційними властивостями ємності
не було, то постійний потенціал затвору визначався б струмами затвору та ізоляційними властивостями ємності 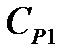 і мав би непередбачуване значення. Величина
і мав би непередбачуване значення. Величина 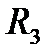 повинна бути значно більшою від реактивного опору ємності
повинна бути значно більшою від реактивного опору ємності 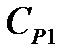 в усьому діапазоні робочих частот і обирається звичайно порядку
в усьому діапазоні робочих частот і обирається звичайно порядку 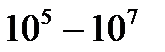 Ом. Опір
Ом. Опір 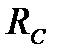 є навантаженням транзистора і на ньому, власне, і виділяється підсилений сигнал.
є навантаженням транзистора і на ньому, власне, і виділяється підсилений сигнал.
|
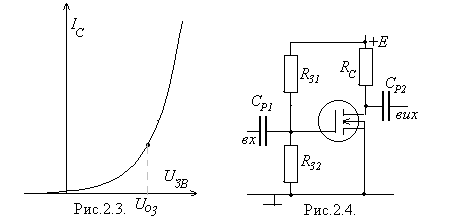
Для успішної роботи МДН - транзистора з індукованим 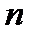 - каналом на затвор слід подати позитивне зміщення (рис.2.3). А оскільки напруга джерела живлення такого транзистора також позитивна, то скориставшись подільником
- каналом на затвор слід подати позитивне зміщення (рис.2.3). А оскільки напруга джерела живлення такого транзистора також позитивна, то скориставшись подільником 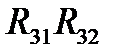 можна від того ж джерела одержати потрібну напругу зміщення (рис.2.4). З того ж. Що струм затвору звичайно дуже малий, висновується, що ці опори подільника можуть бути досить великим (порядку МОм).
можна від того ж джерела одержати потрібну напругу зміщення (рис.2.4). З того ж. Що струм затвору звичайно дуже малий, висновується, що ці опори подільника можуть бути досить великим (порядку МОм).
| 
|
В польовому транзисторі з керуючим 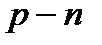 переходом та
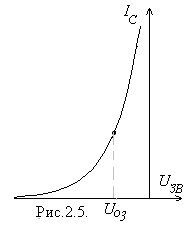
переходом та 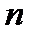 - каналом на затвор слід подавати від’ємну напругу (рис.2.5). Для цього можна було б скористатися схемою, зображеною на рис. 2.2, увімкнувши послідовно з опором
- каналом на затвор слід подавати від’ємну напругу (рис.2.5). Для цього можна було б скористатися схемою, зображеною на рис. 2.2, увімкнувши послідовно з опором 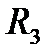 джерело е.р.с., яке забезпечувало
джерело е.р.с., яке забезпечувало  б подачу на затвор потрібної від’ємної напруги
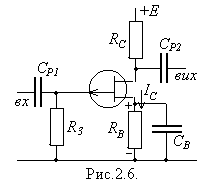
б подачу на затвор потрібної від’ємної напруги 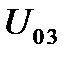 . Але потреба ще в одному джерелі живлення вельми небажана. Тому звичайно застосовують так зване «автоматичне зміщення» (рис.2.6). Тут затвор має нульовий постійний потенціал. Зате витік перебуває відносно землі під постійною позитивною напругою, яка створюється внаслідок протікання струму
. Але потреба ще в одному джерелі живлення вельми небажана. Тому звичайно застосовують так зване «автоматичне зміщення» (рис.2.6). Тут затвор має нульовий постійний потенціал. Зате витік перебуває відносно землі під постійною позитивною напругою, яка створюється внаслідок протікання струму 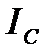 через опір
через опір 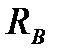 , увімкнений в коло витоку. Величина опору
, увімкнений в коло витоку. Величина опору 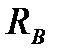 підбирається такою, щоб спад напруги на ньому дорівнював
підбирається такою, щоб спад напруги на ньому дорівнював 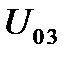 . Тоді затвор буде від’ємнішим за витік на потрібну величину напруги зміщення. А для того, щоб змінна (сигнальна) компонента струму витоку
. Тоді затвор буде від’ємнішим за витік на потрібну величину напруги зміщення. А для того, щоб змінна (сигнальна) компонента струму витоку 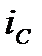 не давала внеску у напругу зміщення. Резистор
не давала внеску у напругу зміщення. Резистор 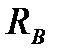 шунтують великою ємністю
шунтують великою ємністю 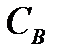 , яка закорочує для змінної компоненти витік на землю.
, яка закорочує для змінної компоненти витік на землю.
Все викладене залишається в силі і для транзисторів з 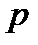 - каналом. Потрібно лише знаки всіх струмів і напруг у наведених вище схемах замінити на протилежні.
- каналом. Потрібно лише знаки всіх струмів і напруг у наведених вище схемах замінити на протилежні.
2.2 Коефіцієнт підсилення
|
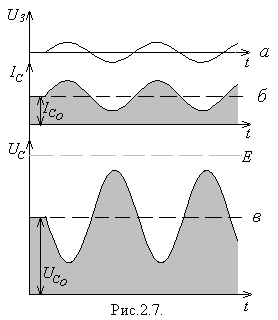
Розглянемо процес підсилення сигналу на прикладі схеми. зображеної на рис.2.2. Нехай напруга на затворі змінюється за законом 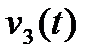 (рис.2.7а) . Постійна компонента затворної напруги для даної схеми дорівнює нулю. Струм у колі стоку
(рис.2.7а) . Постійна компонента затворної напруги для даної схеми дорівнює нулю. Струм у колі стоку 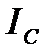 складається з постійної компоненти
складається з постійної компоненти 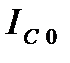 та змінної компоненти
та змінної компоненти 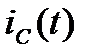 , яка повторює зміни напруги на затворі (рис.27б):
, яка повторює зміни напруги на затворі (рис.27б):
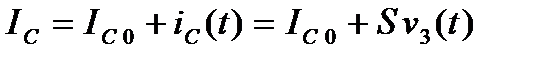
Тут 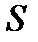 - крутість прохідної характеристики в околі робочої точки.
- крутість прохідної характеристики в околі робочої точки.
Протікаючи через навантажувальний опір 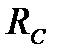 струм
струм 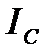 створює на ньому спад напруги; отже, напруга на стоку
створює на ньому спад напруги; отже, напруга на стоку 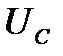 буде нижчою за напругу джерела живлення:
буде нижчою за напругу джерела живлення:
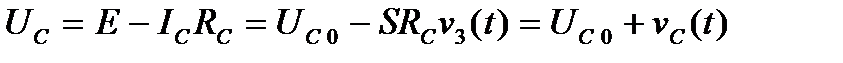 ,
,
де 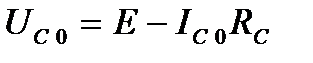 - постійна складова напруги на стоку.
- постійна складова напруги на стоку.
Таким чином, змінна складова 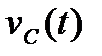 напруги на стоку (тобто на виході каскаду) повторює всі зміни вхідної напруги
напруги на стоку (тобто на виході каскаду) повторює всі зміни вхідної напруги 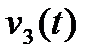 , будучи, однак, збільшеною у
, будучи, однак, збільшеною у 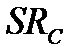 розів та протилежною за знаком (рис.2.7в).
розів та протилежною за знаком (рис.2.7в).
|
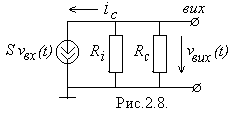
Для більш докладного кількісного розрахунку коефіцієнта підсилення 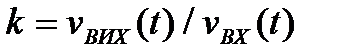 побудуємо еквівалентну схему для змінних компонент струмів і напруг нашого підсилювального каскаду (рис.2.8). тут польовий транзистор зображено як генератор струму
побудуємо еквівалентну схему для змінних компонент струмів і напруг нашого підсилювального каскаду (рис.2.8). тут польовий транзистор зображено як генератор струму 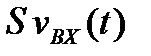 , який керується вхідною напругою (тобто змінною складовою напруги на затворі) і має внутрішній опір
, який керується вхідною напругою (тобто змінною складовою напруги на затворі) і має внутрішній опір 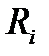 . Паралельно йому увімкнений навантажувальний опір
. Паралельно йому увімкнений навантажувальний опір 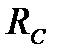 [1]). Вихідна напруга створюється струмом
[1]). Вихідна напруга створюється струмом 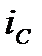 , який протікає через паралельно увімкнені опори
, який протікає через паралельно увімкнені опори 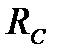 і
і 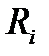 , так що
, так що
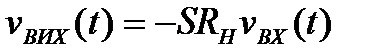
де 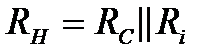 - загальний опір навантаження. Тоді коефіцієнт підсилення виявляється рівним
- загальний опір навантаження. Тоді коефіцієнт підсилення виявляється рівним
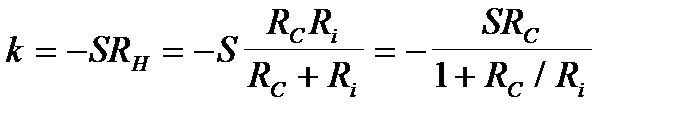 (2.1)
(2.1)
|
Одержаний результат підтверджує зроблену вище оцінку коефіцієнта підсилення і відрізняється лише урахуванням внутрішнього опору транзистора.
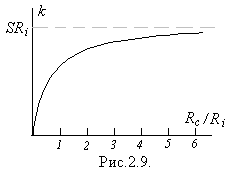
З формули (2.1) видно, що нарощування величини 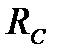 призводить до відповідного зростання коефіцієнта підсилення
призводить до відповідного зростання коефіцієнта підсилення 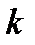 лише доти, доки
лише доти, доки 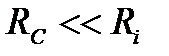 ; при їх сумірності внутрішній опір транзистора починає обмежувати зростання коефіцієнта підсилення. А при
; при їх сумірності внутрішній опір транзистора починає обмежувати зростання коефіцієнта підсилення. А при 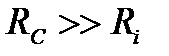 коефіцієнт підсилення прямує до постійної величини, що дорівнює
коефіцієнт підсилення прямує до постійної величини, що дорівнює 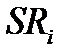 (рис.2.9).
(рис.2.9).
Тому недоцільно, гонячись за великим коефіцієнтом підсилення надмірно збільшувати величину опору 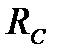 . Більш того, надмірне збільшення цього опору призведе до зменшення режимної компоненти напруги
. Більш того, надмірне збільшення цього опору призведе до зменшення режимної компоненти напруги 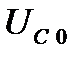 , що доходить до стоку нашого транзистора. А це зашкодить параметрам транзистора, зокрема призведе до зменшення його крутості . Крім того, як ми це побачимо далі, збільшення опору навантаження призводить до погіршення роботи підсилювального каскаду у області високих частот.
, що доходить до стоку нашого транзистора. А це зашкодить параметрам транзистора, зокрема призведе до зменшення його крутості . Крім того, як ми це побачимо далі, збільшення опору навантаження призводить до погіршення роботи підсилювального каскаду у області високих частот.
2.3. Частотна характеристика
Частотною характеристикою підсилювача називається залежність коефіцієнта підсилення - його модуля та фази - від частоти. Відповідно, залежність абсолютної величини (модуля) коефіцієнта підсилення від частоти 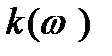 має назву амплітудно-частотної характеристики (АЧХ), а залежність створюваного підсилювачем повороту фази підсилюваного гармонічного сигналу від частоти
має назву амплітудно-частотної характеристики (АЧХ), а залежність створюваного підсилювачем повороту фази підсилюваного гармонічного сигналу від частоти 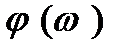 - фазово-частотною характеристикою (ФЧХ). Частотна характеристика містить вельми важливу інформацію про підсилювач, оскільки вказує в якому діапазоні частот він може успішно працювати та які спотворення вносить він у спектр підсилюваних сигналів.
- фазово-частотною характеристикою (ФЧХ). Частотна характеристика містить вельми важливу інформацію про підсилювач, оскільки вказує в якому діапазоні частот він може успішно працювати та які спотворення вносить він у спектр підсилюваних сигналів.
2.3.1. Частотна характеристика в області високих частот
Очевидно, що підсилювач на може підсилювати як завгодно високі частоти і при 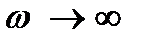 коефіцієнт підсилення має прямувати до нуля. Конкретні причини, які обмежують здатність підсилювача підсилювати сигнали високих частот можуть бути притаманні як самому транзистору (його інерційність), так і схемі підсилювача. Для польових транзисторів характерний час їх інерційності малий і становить
коефіцієнт підсилення має прямувати до нуля. Конкретні причини, які обмежують здатність підсилювача підсилювати сигнали високих частот можуть бути притаманні як самому транзистору (його інерційність), так і схемі підсилювача. Для польових транзисторів характерний час їх інерційності малий і становить 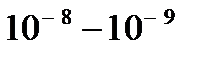 с, отже основна причина в цьому випадку криється в інерційності самої схеми.
с, отже основна причина в цьому випадку криється в інерційності самої схеми.
Головним чинником, який визначає хід частотної характеристики підсилювача в області високих частот, є величина вихідної ємності каскаду 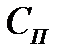 (яку іноді називають «паразитною» ємністю), що завжди існує між стоком транзистора і землею. Ця ємність, звичайно, не зображується на схемі, але завжди в ній невидимо присутня. Паразитна ємність складається з вихідної ємності транзистора, вхідної ємності пристрою, підключеного до виходу підсилювача(наприклад, вхідної ємності наступного каскаду), ємності монтажу, а її величина звичайно вкладається в межі від одиниць до кількох десятків пікофарад.
(яку іноді називають «паразитною» ємністю), що завжди існує між стоком транзистора і землею. Ця ємність, звичайно, не зображується на схемі, але завжди в ній невидимо присутня. Паразитна ємність складається з вихідної ємності транзистора, вхідної ємності пристрою, підключеного до виходу підсилювача(наприклад, вхідної ємності наступного каскаду), ємності монтажу, а її величина звичайно вкладається в межі від одиниць до кількох десятків пікофарад.
Тепер навантаженням джерела струму, зображеного на еквівалентній схемі рис.2.8. є вже не 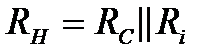 , а паралельне сполучення
, а паралельне сполучення 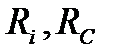 та ємності
та ємності 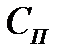 . Повний комплексний опір такого навантаження становить
. Повний комплексний опір такого навантаження становить
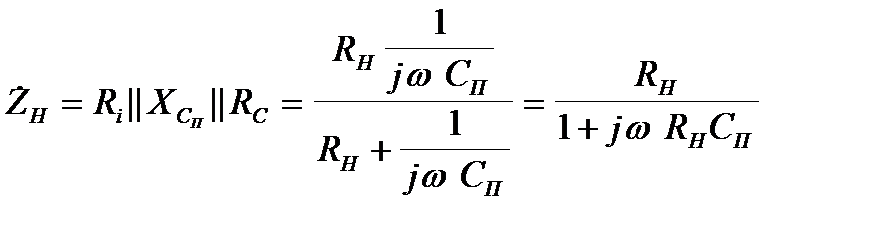 (2.2)
(2.2)
Відповідно, коефіцієнт підсилення буде тепер також комплексним і матиме такий вигляд:
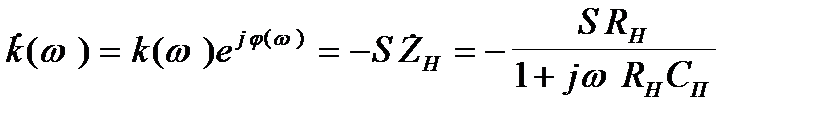 (2.3)
(2.3)
Модуль його дорівнює
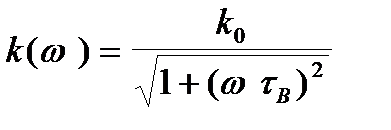 (2.4)
(2.4)
де 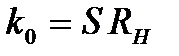 - модуль коефіцієнту підсилення на досить низьких частотах. Коли можна нехтувати шунтуючою дією ємності
- модуль коефіцієнту підсилення на досить низьких частотах. Коли можна нехтувати шунтуючою дією ємності 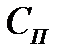 (тобто коли
(тобто коли 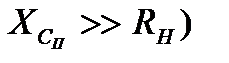 ;
; 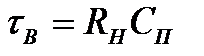 - стала часу вихідного кола підсилювача. вираз (2.4) і є амплітудно-частотною характеристикою нашого підсилювача, її графік зображено на рис 2.10а. В області низьких частот
- стала часу вихідного кола підсилювача. вираз (2.4) і є амплітудно-частотною характеристикою нашого підсилювача, її графік зображено на рис 2.10а. В області низьких частот 
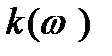 не залежить від частоти і лишається рівним
не залежить від частоти і лишається рівним 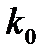 . На високих частотах АЧХ починає монотонно знижуватися і асимптотично прямує до вісі абсцис. Звичайно, неможливо вказати певну граничну частоту. Починаючи з підсилювач раптом перестає підсилювати сигнали: крива
. На високих частотах АЧХ починає монотонно знижуватися і асимптотично прямує до вісі абсцис. Звичайно, неможливо вказати певну граничну частоту. Починаючи з підсилювач раптом перестає підсилювати сигнали: крива 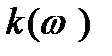 спадає досить плавно. Умовно за таку граничну частоту звичайно приймають частоту
спадає досить плавно. Умовно за таку граничну частоту звичайно приймають частоту 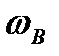 , на якій модуль коефіцієнту підсилення зменшується в
, на якій модуль коефіцієнту підсилення зменшується в 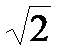 раз порівняно з
раз порівняно з 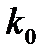 . Ця частота вважається верхньою границею смуги пропускання підсилювача і дорівнює
. Ця частота вважається верхньою границею смуги пропускання підсилювача і дорівнює
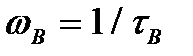 . (2.5)
. (2.5)
Так наприклад, для типових значень 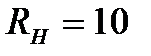 кОм та
кОм та 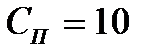 пФ, ця частота дорівнює
пФ, ця частота дорівнює 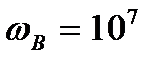 с-1, що відповідає
с-1, що відповідає 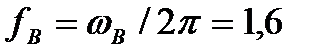 МГц.
МГц.
Величина 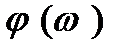 вказує на той зсув по фазі, який зазнає гармонічний сигнал з частотою
вказує на той зсув по фазі, який зазнає гармонічний сигнал з частотою 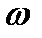 при проходженні через підсилювач. Графік залежності
при проходженні через підсилювач. Графік залежності 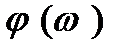 подано на рис.2.10б. як видно, на досить низьких частотах (де
подано на рис.2.10б. як видно, на досить низьких частотах (де 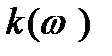 можна вважати незмінним) маємо
можна вважати незмінним) маємо 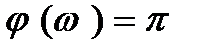 : підсилювач обертає фазу на 1800. На це вказує знак мінус перед виразом (2.3). На високих частотах до цього значення додається ще й зсув фази
: підсилювач обертає фазу на 1800. На це вказує знак мінус перед виразом (2.3). На високих частотах до цього значення додається ще й зсув фази 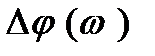 , обумовлений комплексним характером навантаження, Зсув фази може бути обчислений як арктангенс відношення уявної частини виразу
, обумовлений комплексним характером навантаження, Зсув фази може бути обчислений як арктангенс відношення уявної частини виразу 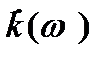 до його дійсної частини:
до його дійсної частини:
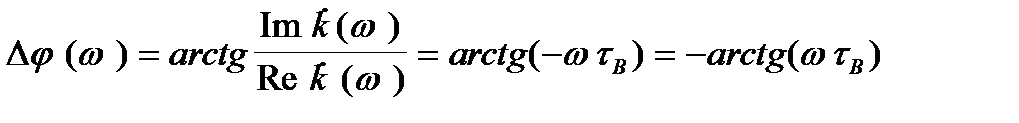 (2.6)
(2.6)
Отже, при 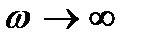 цей поворот фази прямує до -900, і таким чином повний поворот фази прямує до +900. На частоті
цей поворот фази прямує до -900, і таким чином повний поворот фази прямує до +900. На частоті 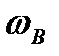 повний поворот фази становить 1350.
повний поворот фази становить 1350.
2.3.2. Частотна характеристика в області низьких частот
|
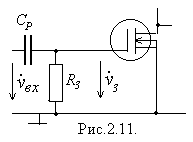
В підсилювачах, призначених для підсилення змінної напруги, на вході звичайно ставиться розділова ємність 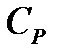 , яка захищає вхід транзистора від можливого порушення його режиму (по постійним складовим) з боку пристроїв, що можуть бути приєднані до входу підсилювача (рис.2.11). Саме ця ємність і дає основний внесок в частотну залежність коефіцієнта підсилення в області низьких частот. Дійсно, для сигналів досить низьких частот розділова ємність являє собою великий реактивний опір, який просто не пропускає ці сигнали на затвор транзистора. Тому в таких підсилювачах
, яка захищає вхід транзистора від можливого порушення його режиму (по постійним складовим) з боку пристроїв, що можуть бути приєднані до входу підсилювача (рис.2.11). Саме ця ємність і дає основний внесок в частотну залежність коефіцієнта підсилення в області низьких частот. Дійсно, для сигналів досить низьких частот розділова ємність являє собою великий реактивний опір, який просто не пропускає ці сигнали на затвор транзистора. Тому в таких підсилювачах 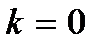 при
при 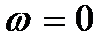 . Вхідне коло подібного транзистора являє собою подільник напруги, який складається з ємності
. Вхідне коло подібного транзистора являє собою подільник напруги, який складається з ємності 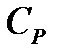 та опору
та опору 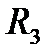 і має коефіцієнт ділення
і має коефіцієнт ділення
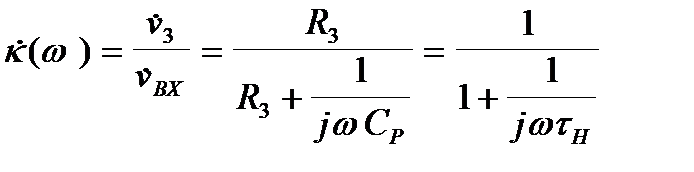 (2.7)
(2.7)
де 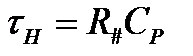 - стала часу кола подільника. Далі сигнал підсилюється звичайним шляхом і загальний коефіцієнт підсилення каскаду
- стала часу кола подільника. Далі сигнал підсилюється звичайним шляхом і загальний коефіцієнт підсилення каскаду 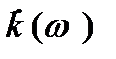 дорівнюватиме
дорівнюватиме

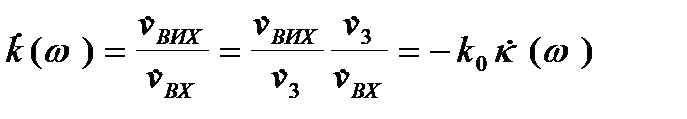 (2.8)
(2.8)
де 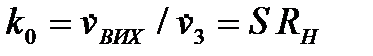 - коефіцієнт підсилення «чистого» підсилювача, визначений вище.
- коефіцієнт підсилення «чистого» підсилювача, визначений вище.
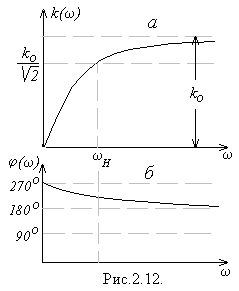
Таким чином, всі особливості ходу АЧХ та ФЧХ в області низьких частот визначаються вхідним  - колом підсилювача. Аналітично ці особливості описуються залежностями
- колом підсилювача. Аналітично ці особливості описуються залежностями
|
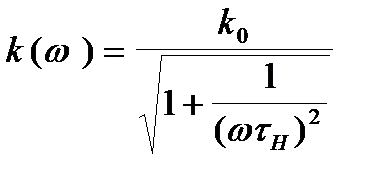 (2.9)
(2.9)
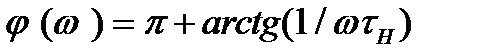 (2.10)
(2.10)
і мають вигляд, зображений на рис.2.12а та 2.12б. Як видно, амплітудно-частотна характеристика починається з початку координат і монотонно зростає, прямуючи до 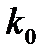 . За умовну границю, починаючи з якої підсилювач може успішно підсилювати сигнали, приймається частота
. За умовну границю, починаючи з якої підсилювач може успішно підсилювати сигнали, приймається частота 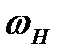 , при якій коефіцієнт підсилення становить
, при якій коефіцієнт підсилення становить 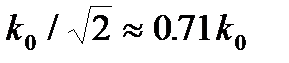 . Ця частота дорівнює
. Ця частота дорівнює
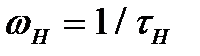 (2.11)
(2.11)
Фазово - частотна характеристика починається від 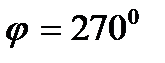 при
при 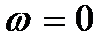 і далі плавно знижується до 1800; на граничній частоті
і далі плавно знижується до 1800; на граничній частоті 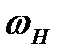 повний поворот фази становить 2250.
повний поворот фази становить 2250.
Слід відзначити, що в схемі з автоматичним зміщенням (рис.2.6) певний внесок у хід частотної характеристики в області низьких частот може давати 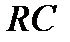 - елемент, увімкнений в коло витоку. Однак при правильному виборі величини
- елемент, увімкнений в коло витоку. Однак при правильному виборі величини 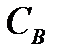 , коли виконана умова
, коли виконана умова 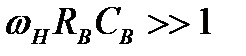 , основну роль відіграє все ж таки вхідне
, основну роль відіграє все ж таки вхідне 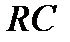 - коло підсилювача
- коло підсилювача
2.3.3. Загальний вигляд частотної характеристики каскаду
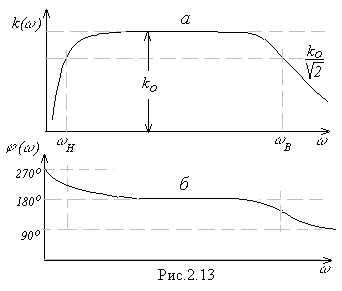
| В цілому частотна характеристика підсилювача є добутком частотної характеристики в області високих частот (2.4) на коефіцієнт ділення вхідного подільника (2.7).Загальний вигляд АЧХ поданий на рис.2.13а. Характеристика складається з трьох частин:
- області зниження («завалу») коефіцієнта підсилення на низьких частотах ( 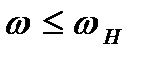 );
- «завалу» в області високих частот ( );
- «завалу» в області високих частот ( 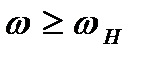 );
- області більш-менш рівномірного підсилення, де );
- області більш-менш рівномірного підсилення, де 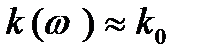 на середніх частотах від на середніх частотах від 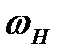 до до 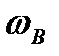 . Саме ця область має назву смуги пропускання підсилювача. . Саме ця область має назву смуги пропускання підсилювача.
|
Фазово - частотна характеристика, зображена на рис.2.13б,одержана шляхом підсумовування поворотів фаз, обумовлених вхідним 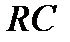 - колом, вихідним
- колом, вихідним 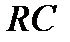 - колом та самим навантаженням транзистора. В області середніх частот поворот фази становить 1800; на нижній та верхній граничних частотах він відрізняється відповідно на
- колом та самим навантаженням транзистора. В області середніх частот поворот фази становить 1800; на нижній та верхній граничних частотах він відрізняється відповідно на 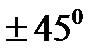 .
.
Для кількісного описання ступеню нерівномірності АЧХ вводиться коефіцієнт нерівномірності 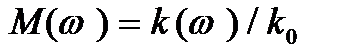 , який являє собою значення модуля коефіцієнта підсилення, нормованого на величину
, який являє собою значення модуля коефіцієнта підсилення, нормованого на величину 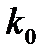 . Іноді коефіцієнт нерівномірності виражають у децибелах (дБ)
. Іноді коефіцієнт нерівномірності виражають у децибелах (дБ)  . Так наприклад, на граничних частотах, де
. Так наприклад, на граничних частотах, де 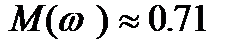 , нерівномірність становитиме мінус 3 дБ. А про область, яка відповідає смузі пропускання підсилювача, кажуть, що нерівномірність в ній не перевищує трьох децибелів.
, нерівномірність становитиме мінус 3 дБ. А про область, яка відповідає смузі пропускання підсилювача, кажуть, що нерівномірність в ній не перевищує трьох децибелів.
Амплітудно-частотна та фазово-частотна характеристики дозволяють судити про зміни, які зазнає сигнал, проходячи через підсилювач. Дійсно, складний сигнал, який має широкий спектр частот, при проходженні через підсилювач зазнаватиме деформацію спектра: одні частоти будуть підсилюватися в більшій мірі, інші, у порівняння з ними будуть придушуватися. Окрім того, за рахунок різної величини зсуву фаз на різних частотах одні частотні складові виявляться зсунутими у часі відносно інших. Наслідком цього, природно, буде спотворення форми сигналу.
За рахунок завалу верхніх частот форма сигналу згладжується, щезає його тонка часова структура. При відтворенні на слух подібний сигнал сприймається як глухий, басовитий. А при придушенні низьких частот зникають повільні зміни сигналу, зберігаються лише його швидкі стрибки та осциляції. Звучання такого сигналу сприймається як різке і пискляве.
Слід, однак, підкреслити, що за рахунок частотних спотворень в спектрі сигналу нові частоти не з’являються - відбувається лише перерозподіл амплітуд та фаз тих гармонічних компонентів, які вже існували у вхідному сигналі. Такі спотворення називають лінійними, на відміну від нелінійних спотворень, при яких в спектрі сигналу з’являються нові, раніше відсутні частотні компоненти.
2.4. Проходження через підсилювач прямокутного імпульсу.
Перехідні процеси у підсилювачі.
Як саме нерівномірність частотної характеристики відіб’ється на формі сигналу, можна проілюструвати на прикладі періодичного прямокутного імпульсу, що проходить через підсилювач. Для цього треба розкласти прямокутний імпульс на гармонічні частотні складові, врахувати всі ті зміни амплітуди та фази, які ці складові зазнають, проходячи через підсилювач, а потім знову їх скласти. Одначе такий шлях є складним і громіздким, тому ми скористаємося іншим, більш простим і наочним методом, заснованим на розгляді перехідних процесів, які відбуваються при проходженні прямокутного імпульсу через кола нашого підсилювача.
Прямокутний імпульс величиною 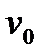 та тривалістю
та тривалістю 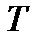 , який поступає на вхід підсилювача в момент
, який поступає на вхід підсилювача в момент 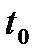 , можна розглядати як суму двох імпульсів увімкнення
, можна розглядати як суму двох імпульсів увімкнення 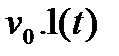 , зсунутих у часі : першого позитивного, що починається в момент
, зсунутих у часі : першого позитивного, що починається в момент 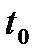 , та другого. Негативного, що починається в момент
, та другого. Негативного, що починається в момент 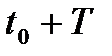 (рис.2.14а)[2]). Після проходження через вхідне
(рис.2.14а)[2]). Після проходження через вхідне 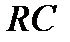 - коло, яке являє собою диференцюючий елемент зі сталою часу
- коло, яке являє собою диференцюючий елемент зі сталою часу 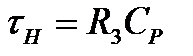 , перший импульс увімкнення перетворюється на експоненціальний імпульс
, перший импульс увімкнення перетворюється на експоненціальний імпульс
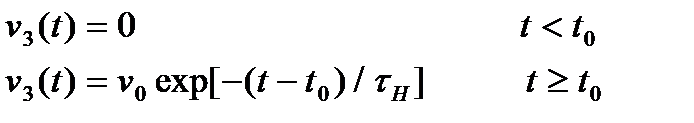 (2.13)
(2.13)
Аналогічно, другий імпульс увімкнення створить на затворі транзистора сигнал
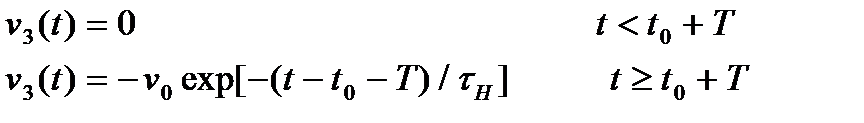 (2.14)
(2.14)
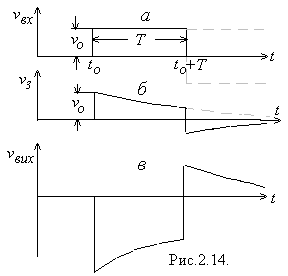
| Їх сума являтиме собою спотворений прямокутний імпульс з різкими фронтами, із скошеню (або, як то кажуть «сколотою») верхівкою і тривалим від’ємним «хвостом» (рис.2.14б). Вихідний сигнал повторюватиме цю форму, будучи, однак, підсиленим за величиною та оберненим за знаком (рис.2.14в).
Скол верхівки та від’ємний хвіст будуть мало помітні, якщо 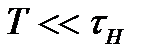 , оскільки напруга на затворі не встигає істотно змінитися за час імпульсу, Взявши до уваги, що T обернено пропорційне , оскільки напруга на затворі не встигає істотно змінитися за час імпульсу, Взявши до уваги, що T обернено пропорційне 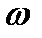 - першій гармоніці нашого імпульсу, а - першій гармоніці нашого імпульсу, а 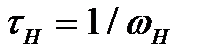 , дійдемо висновку, що вказана вище , дійдемо висновку, що вказана вище
|
нерівність еквівалентна умові 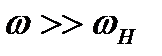 , при якій всі частотні складові сигналу виявляються значно вищими нижньої граничної частоти
, при якій всі частотні складові сигналу виявляються значно вищими нижньої граничної частоти 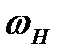 . При цьому сигнал не повинний зазнавати спотворень, що і видно на рис. 2.15а.
. При цьому сигнал не повинний зазнавати спотворень, що і видно на рис. 2.15а.
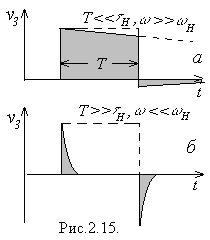
| Якщо ж 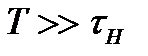 , то перехідний процес від переднього фронту імпульсу закінчиться раніше, ніж сам імпульс дійде до кінця (рис.2.15б). Отже, замість прямокутного імпульсу одержимо гострі викиди - позитивний від переднього фронту та негативний від заднього. Обидва викиди є результатом диференціювання вхідного сигналу. Нерівність , то перехідний процес від переднього фронту імпульсу закінчиться раніше, ніж сам імпульс дійде до кінця (рис.2.15б). Отже, замість прямокутного імпульсу одержимо гострі викиди - позитивний від переднього фронту та негативний від заднього. Обидва викиди є результатом диференціювання вхідного сигналу. Нерівність 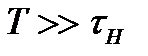 еквівалентна нерівності еквівалентна нерівності 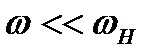 , при якій нижні гармоніки сигналу опиняються поза межами смуги пропускання і придушуються, а верхні. що залишилися, утворюють вельми спотворену картину. , при якій нижні гармоніки сигналу опиняються поза межами смуги пропускання і придушуються, а верхні. що залишилися, утворюють вельми спотворену картину.
| |
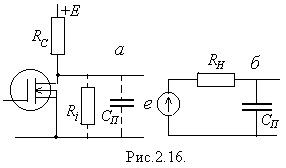
| Джерелом спотворень в області високих частот є вихідне 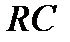 - коло, яке складається з навантажувального опору - коло, яке складається з навантажувального опору 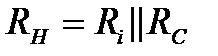 та паразитної ємності та паразитної ємності 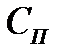 (рис.2.16а). Для зручності аналізу це (рис.2.16а). Для зручності аналізу це 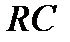 - коло можна зобразити у вигляді еквівалентного генератора напруги - коло можна зобразити у вигляді еквівалентного генератора напруги 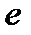 з внутрішнім опором з внутрішнім опором 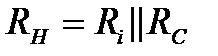 , навантаженого на паразитну ємність , навантаженого на паразитну ємність 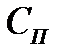 (рис.2.16б)[3]). (рис.2.16б)[3]).
| |
У такому вигляді вихідне коло підсилювача виявляється зведеним до інтегруючого елемента зі сталою часу 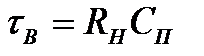 .
.
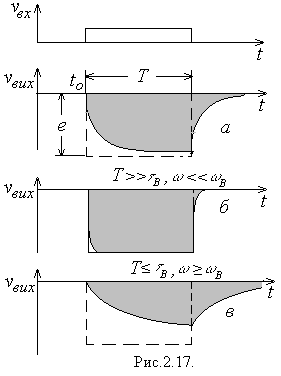
| Уявимо, як і раніш, вхідний прямокутний імпульс у вигляді двох зсунутих у часі імпульсів увімкнення. Кожному з них на виході підсилювача відповідатиме імпульс напруги 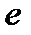 підсилений в підсилений в 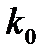 разів за величиною та інвертований за полярністю. Перехідний процес, який відповідатиме першому фронту імпульсу може бути представлений у вигляді: разів за величиною та інвертований за полярністю. Перехідний процес, який відповідатиме першому фронту імпульсу може бути представлений у вигляді:
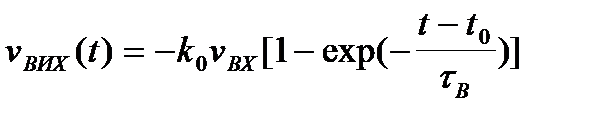 (2.15)
Аналогічний вигляд (але зсунутий у часі на (2.15)
Аналогічний вигляд (але зсунутий у часі на 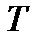 і протилежний за знаком), має і перехідний процес від заднього фронту імпульсу. В результаті вихідний сигнал набуває вигляду імпульсу з пологим переднім фронтом та затягнутим заднім (рис.2.17а). і протилежний за знаком), має і перехідний процес від заднього фронту імпульсу. В результаті вихідний сигнал набуває вигляду імпульсу з пологим переднім фронтом та затягнутим заднім (рис.2.17а).
|
При 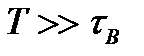 перехідний процес зарядки паразитної ємності через опір
перехідний процес зарядки паразитної ємності через опір 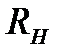 закінчується за час, значно менший від
закінчується за час, значно менший від 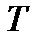 (рис.2.17б), так що вихідна напруга залишається майже незмінною протягом усього імпульсу, і спотворення його форми буде майже непомітним. Саме це відповідає випадку
(рис.2.17б), так що вихідна напруга залишається майже незмінною протягом усього імпульсу, і спотворення його форми буде майже непомітним. Саме це відповідає випадку 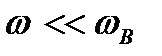 , коли не повинно бути частотних спотворень.
, коли не повинно бути частотних спотворень.
Якщо ж 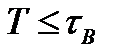 , то перехідний процес затягується на весь час існування імпульсу (рис.2.17в). Вихідна напруга повільно знижуватиметься протягом всього імпульсу і таким же темпом відновлятиметься після його закінчення. Вихідний імпульс матиме не прямокутну, а скоріше трикутну форму - результат його інтегрування вихідним
, то перехідний процес затягується на весь час існування імпульсу (рис.2.17в). Вихідна напруга повільно знижуватиметься протягом всього імпульсу і таким же темпом відновлятиметься після його закінчення. Вихідний імпульс матиме не прямокутну, а скоріше трикутну форму - результат його інтегрування вихідним 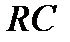 - колом підсилювача. Цей випадок відповідає умові
- колом підсилювача. Цей випадок відповідає умові 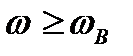 , тобто випадку, коли частоти всіх гармонічних складових сигналу лежать вище верхньої граничної частоти підсилювача.
, тобто випадку, коли частоти всіх гармонічних складових сигналу лежать вище верхньої граничної частоти підсилювача.
2.5. Корекція частотних характеристик
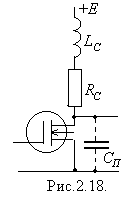
| Рівномірність частотної характеристики можна дещо поліпшити нескладним схемотехнічними заходами. Вище зазначалося, що зниження коефіцієнта підсилення в області високих частот обумовлене зменшенням повного опору навантаження внаслідок шунтуючої дії паразитної ємності. Це зменшення можна компенсувати, зробивши так, щоб повний опір елементу 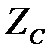 (яким ми тепер заміняємо резистор (яким ми тепер заміняємо резистор 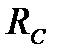 ) зростав з частотою. Таким елементом може бути індуктивність. Тому для корекції частотної характеристики в області високих частот послідовно з резистором ) зростав з частотою. Таким елементом може бути індуктивність. Тому для корекції частотної характеристики в області високих частот послідовно з резистором 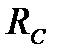 слід увімкнути індуктивність слід увімкнути індуктивність 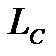 (рис.2.18). Тепер повний опір навантаження (рис.2.18). Тепер повний опір навантаження 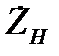 складатиметься з індуктивність складатиметься з індуктивність 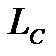 (рис.2.18). Тепер повний опір навантаження (рис.2.18). Тепер повний опір навантаження 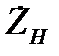 складатиметься з двох складатиметься з двох
|
паралельних гілок: 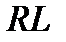 - гілки з опором
- гілки з опором 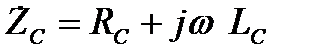 та гілки паразитної ємності з опором
та гілки паразитної ємності з опором 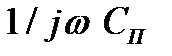 [4]).
[4]).
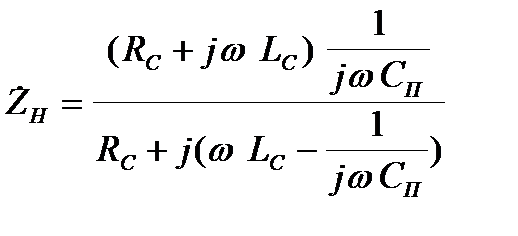 (2.16)
(2.16)
Знаходження модулю 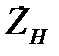 , який для даної схеми визначає АЧХ та її нерівномірність, нескладна, але громіздка операція. Тому одразу наведемо вираз для нерівномірності цієї АЧХ:
, який для даної схеми визначає АЧХ та її нерівномірність, нескладна, але громіздка операція. Тому одразу наведемо вираз для нерівномірності цієї АЧХ:
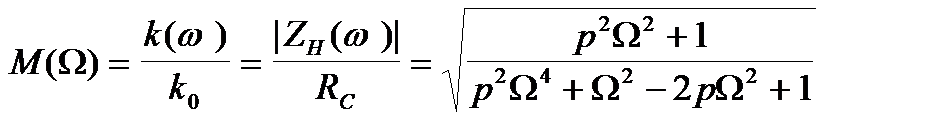 (2.17)
(2.17)
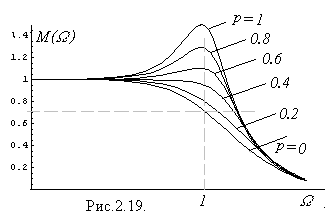
| де 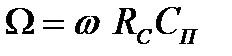 - безрозмірна частота, - безрозмірна частота, 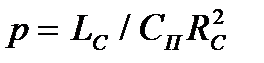 - безрозмірний параметр, пропорційний індуктивності, - безрозмірний параметр, пропорційний індуктивності, 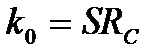 - коефіцієнт підсилення в області середніх частот. Графік - коефіцієнт підсилення в області середніх частот. Графік 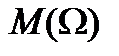 для різних значень параметра для різних значень параметра 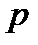 поданий на рис.2.19. Крива для поданий на рис.2.19. Крива для 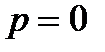 відповідає невідкореганому підсилювачу і перетинає рівень відповідає невідкореганому підсилювачу і перетинає рівень 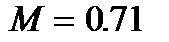 при при 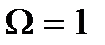 . Із зростанням параметра . Із зростанням параметра 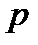 до до 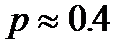 криві зберігають монотонність, криві зберігають монотонність,
|
перетинаючи вказаний рівень при все більших значеннях  .Але вже при
.Але вже при 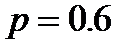 залежність
залежність 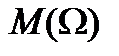 стає немонотонною: на ній з’являється горб, яки при подальшому зростанні
стає немонотонною: на ній з’являється горб, яки при подальшому зростанні 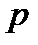 стає все більш високим. Оптимальним буде, очевидно, значення
стає все більш високим. Оптимальним буде, очевидно, значення 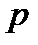 , що відповідає кривій, яка є пограничною між областями монотонного і немонотонного ходу кривих. Щоб відшукати таку криву слід насамперед визначити частоту, на якій
, що відповідає кривій, яка є пограничною між областями монотонного і немонотонного ходу кривих. Щоб відшукати таку криву слід насамперед визначити частоту, на якій 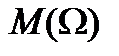 має максимум. Вона виявляється рівною
має максимум. Вона виявляється рівною
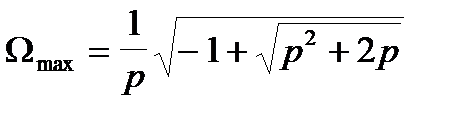
При малих значеннях 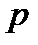 (тобто при
(тобто при 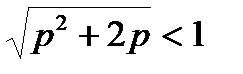 ) ця частота буде уявною і, отже, максимум відсутній. При
) ця частота буде уявною і, отже, максимум відсутній. При 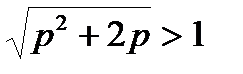 вираз під радикалом позитивний і максимум має місце. Граничним є випадок, коли
вираз під радикалом позитивний і максимум має місце. Граничним є випадок, коли 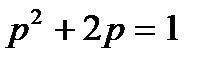 . Це відповідає значенню
. Це відповідає значенню 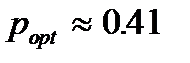 . Для такого значення
. Для такого значення 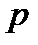 крива перетинає рівень 0.71 при
крива перетинає рівень 0.71 при 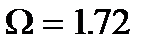 , тобто при оптимальній корекції верхня гранична частота зростає майже вдвічі.
, тобто при оптимальній корекції верхня гранична частота зростає майже вдвічі.
Знизити нижню граничну частоту 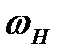 простіше за все збільшенням розділової ємності
простіше за все збільшенням розділової ємності 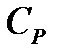 . Однак в деяких випадках для корекції АЧХ в області нижніх частот застосовується схема, зображена на рис.2.20. Тут послідовно з
. Однак в деяких випадках для корекції АЧХ в області нижніх частот застосовується схема, зображена на рис.2.20. Тут послідовно з 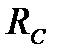 увімкнуто фільтр нижніх частот, що складається з опору
увімкнуто фільтр нижніх частот, що складається з опору 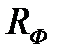 та ємності
та ємності 
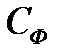 . На найнижчих частотах, для яких можна знехтувати відгалуженням струму через
. На найнижчих частотах, для яких можна знехтувати відгалуженням струму через 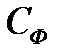 , опір навантаження буде дорівнювати
, опір навантаження буде дорівнювати 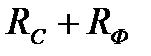 , що забезпечує підвищений коефіцієнт підсилення каскаду
, що забезпечує підвищений коефіцієнт підсилення каскаду 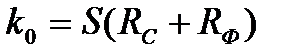 . На більш високих частотах вступає в дію ємність
. На більш високих частотах вступає в дію ємність 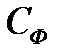 , яка закорочує на землю точку А, так що опір навантаження стає рівним
, яка закорочує на землю точку А, так що опір навантаження стає рівним 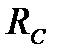 , а коефіцієнт підсилення знижується до звичайного рівня
, а коефіцієнт підсилення знижується до звичайного рівня 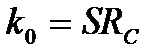 . Частотна характеристика повинна була б мати вигляд, показаний пунктирною лінією
. Частотна характеристика повинна була б мати вигляд, показаний пунктирною лінією 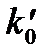 на рис.2.21 - з монотонним підйомом в бік низьких частот. В дійсності ж зі зниженням частоти починає відчуватися дія вхідного подільника, що складається з розділової ємності
на рис.2.21 - з монотонним підйомом в бік низьких частот. В дійсності ж зі зниженням частоти починає відчуватися дія вхідного подільника, що складається з розділової ємності 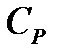 та опору
та опору 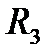 . Нагадаємо, що коефіцієнт ділення цього подільника
. Нагадаємо, що коефіцієнт ділення цього подільника 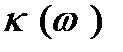 прямує до нуля при
прямує до нуля при 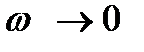 . Тому зображений на рис.2.21 підйом повинен зі зниженням частоти перетворитися на спад і залежність
. Тому зображений на рис.2.21 підйом повинен зі зниженням частоти перетворитися на спад і залежність 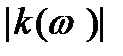 може виявитися немонотонною ( крива 3).
може виявитися немонотонною ( крива 3).
Для оптимальної корекції АЧХ в області низьких частот обирають такі значення 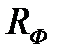 та
та 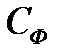 , при яких АЧХ ще залишається монотонною, але сильно зсунутою в бік низьких частот (крива 2 на рис. 2.21). Оптимальна гранична частота
, при яких АЧХ ще залишається монотонною, але сильно зсунутою в бік низьких частот (крива 2 на рис. 2.21). Оптимальна гранична частота 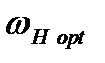 , яка при цьому одержується, може бути у кілька разів нижча за граничну частоту
, яка при цьому одержується, може бути у кілька разів нижча за граничну частоту 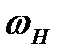 у відсутності корекції ( крива 2).
у відсутності корекції ( крива 2).
Окрім корегування АЧХ фільтр 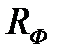
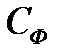 дає ще один позитивний ефект: він не пропускає змінних складових струму ні від каскаду до джерела живлення, ні від джерела до каскаду. Цим виключається можливість зв’язків між каскадами через джерело живлення, що, як ми побачимо далі, може призвести до нестійкості і самозбудження багатокаскадного підсилювача.
дає ще один позитивний ефект: він не пропускає змінних складових струму ні від каскаду до джерела живлення, ні від джерела до каскаду. Цим виключається можливість зв’язків між каскадами через джерело живлення, що, як ми побачимо далі, може призвести до нестійкості і самозбудження багатокаскадного підсилювача.
2.6. Нелінійні спотворення
| Основним завданням, яке ставиться перед будь-яким підсилювачем радіосигналів, є відтворення на виході вхідного сигналу у підсиленому вигляді, але при умові точного збереження його форми. Тобто вихідний сигнал має бути точно пропорційним до вхідного, де коефіцієнт пропорційності і є саме коефіцієнтом підсилення. Як вже відзначалося вище, коефіцієнт підсилення дорівнює 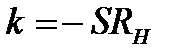 , де , де 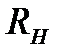 - це опір навантаження, а - це опір навантаження, а 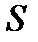 - крутість транзистора. Але крутість транзистора - це похідна його прохідної характеристики і вона істотно залежить від базово-емітерної, тобто вхідної напруги транзистора. - крутість транзистора. Але крутість транзистора - це похідна його прохідної характеристики і вона істотно залежить від базово-емітерної, тобто вхідної напруги транзистора.
|
Вважати крутість незмінною величиною можна лише на коротких ділянках прохідної характеристики. Отже, коефіцієнт підсилення може вважатися незмінним і забезпечувати пропорційність вхідних і вихідних сигналів можна лише у разі, коли сам вхідний сигнал є досить малою величиною.
Що ж до великих вхідних сигналів, то там треба вже враховувати викривленість прохідної характеристики, і вихідний сигнал перестає вже бути пропорційним до вхідного. Спотворення, які він зазнає, мають назву нелінійних спотворень, оскільки їх причиною є нелінійності на шляху проходження підсилюваного сигналу.
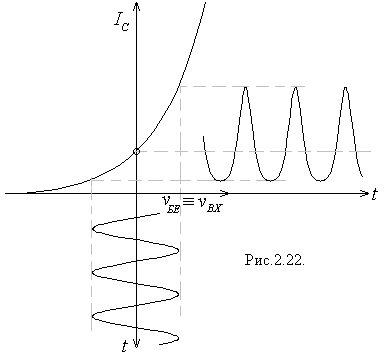
Виникнення нелінійних спотворень ілюструє рис.2.22. Зображена на ньому побудова, подібна до тих, з якими ми будемо нещораз зустрічатися в нашому курсі, має такий сенс: на нижній половині рисунку у координатах 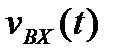 зображено вхідний сигнал, який у даному випадку вважається синусоідальним. На верхній частині рисунку наведена типова прохідна характеристика
зображено вхідний сигнал, який у даному випадку вважається синусоідальним. На верхній частині рисунку наведена типова прохідна характеристика 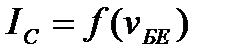 . Вхідний сигнал проектується на цю характеристику і в результаті ми одержуємо залежність
. Вхідний сигнал проектується на цю характеристику і в результаті ми одержуємо залежність 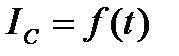 , тобто графік струму, що протікає у колі стоку і дає пропорційний йому вихідний сигнал
, тобто графік струму, що протікає у колі стоку і дає пропорційний йому вихідний сигнал 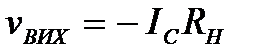 . Як видно, в результаті проектування синусоідального вхідного сигналу на непрямолінійну прохідну характеристику стоковий струм (і разом з ним вихідний сигнал) втрачає вигляд гармонічної функції: його верхня частина витягується вверх і загострюється, а нижня, навпаки, стає більш короткою і закругленою.
. Як видно, в результаті проектування синусоідального вхідного сигналу на непрямолінійну прохідну характеристику стоковий струм (і разом з ним вихідний сигнал) втрачає вигляд гармонічної функції: його верхня частина витягується вверх і загострюється, а нижня, навпаки, стає більш короткою і закругленою.
Така періодична, але негармонічна функція може розглядатися як сума цілої низки гармонічних сигналів як з основною частотою (перша гармоніка), яку мав вхідний сигнал, так і вищих гармонік цього сигналу. Отже, нелінійні спотворення на відміну від вищезгаданих лінійних спотворень призводять до виникненні у спектрі підсиленого сигналу нових частотних компонент, яких не було у вхідному сигналі. Нелінійні спотворення небажані саме тим. що вони, викривлюючи форму підсилюваного сигналу, «засмічують» його спектр новими частотними компонентами.
Для зменшення нелінійних спотворень слід обирати положення робочої точки на прохідній характеристиці в області, де вона є найбільш прямолінійною і не допускати надто великих амплітуд вхідних сигналів, які б виходили за межі ділянки прохідної характеристики, котру можна було б вважати більш-менш прямолінійною.
[1] Оскільки позитивний провідник джерела живлення зберігає свій потенціал незмінним у часі і рівним +Е, можна вважати, що за змінною складовою він знаходиться під потенціалом землі. Ому при розрахунках за змінними складовими верхній кінець опору 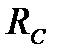 можна вважати заземленим. Практично це забезпечується мализною внутрішнього опору джерела живлення для змінних компонент. .
можна вважати заземленим. Практично це забезпечується мализною внутрішнього опору джерела живлення для змінних компонент. .
[2] Імпульсом увімкнення в радіоелектроніці називають функцію, яка являє собою миттєвий стрибок в момент t від нуля до одиничного значення. Цю функцію позначають як 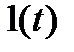 і інколи в іноземній літературі називають функцією Хевісайда.
і інколи в іноземній літературі називають функцією Хевісайда.
[3] Це є звичайний перехід від генератора струму до еквівалентного йому генератора напруги.
[4] Внутрішнім опором транзистора для спрощення розрахунків ми тут нехтуємо, вважаючи його дуже великим 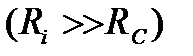 . В разі необхідності його можна врахувати шляхом перерахунку паралельно сполучених
. В разі необхідності його можна врахувати шляхом перерахунку паралельно сполучених 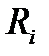 та
та 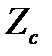 в єдину еквівалентну гілку, яка містить послідовно сполучені
в єдину еквівалентну гілку, яка містить послідовно сполучені 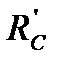 та
та 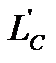 .
. 
| <== предыдущая лекция | | | следующая лекция ==> |
| Операційний підсилювач | | | СОЮЗ ЧЕЛОВЕКА И СОБАКИ |
Дата добавления: 2016-04-19; просмотров: 3989;
