на біполярному транзисторі

Частотні властивості підсилювача

Аналізуючи частотні властивості підсилювача на біполярному транзисторі нам доводиться рівною мірою враховувати як вплив реактивних параметрів схеми (вихідну ємність каскаду), так і інерційність самого транзистора. Тому в цьому випадку аналіз виявляється значно складнішим порівняно з аналізом підсилювача на польовому транзисторі, де основна роль у формуванні частотних властивостей належить реактивним параметрам схеми.

3.5.1. Еквівалентна схема підсилювача в області високих частот

Для побудови еквівалентної схеми підсилювача на біполярному транзисторі скористуємося розглянутою раніш фізичною еквівалентною схемою Джіоколетто (рис.3.8).

Тут джерело вхідного сигналу зображене у вигляді генератора ЕРС з внутрішнім опором . Навантаження представлено резистором , який може бути зашунтованим вихідною (паразитною) ємністю 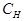. Ємність 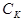є бар’єрною ємністю базово - колекторного переходу транзистора. Інерційні властивості транзистора, обумовлені скінченим часом руху носіїв у базі, моделюються ємністю 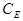, яка зв’язана з граничною частотою транзистора 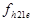співвідношенням

Опір 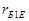зображає диференціальний опір емітерно - базового переходу, а 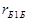- поперечний опір бази.

Величина вхідної напруги , прикладеної до бази транзистора (на низьких та середніх частотах, де роллю ємностей можна знехтувати), пов’язана з ЕРС джерела сигналу як

, де . (3.26)

Вона менше від ЕРС джерела , бо послаблюється дільником, що складається з активних опорів, як існують на вході транзистора.

Струм 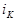у вихідному колі створюється генератором струму 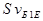, який керується напругою 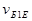. Вихідна напруга протифазна до вхідної і дорівнює

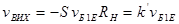, (3.27)

де - еквівалентний навантажувальний опір, а - внутрішній коефіцієнт підсилення між виходом, тобто колектором та ефективною базою - тобто точкою Б1. Що ж до 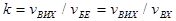, то його можна назвати зовнішнім коефіцієнтом підсилення, який завжди менший від внутрішнього

. (3.28)

Розв’язання нашої задачі почнемо з перетворення схеми зображеної на рис.3.8 таким чином, щоб позбутися елементів і 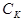, які зв’язують вхідне та вихідне кола транзистора, і звести її до виду подібного до еквівалентної схеми транзистора для 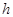або 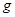параметрів (див рис. або ч І).

Елементи і 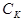увімкнено між виходом і ефективною базою нашого підсилювача і вони створюють таким чином внутрішній паралельний негативний зворотний зв’язок, що його було розглянуто у попередніх розділах. Як там було доведено, при негативному паралельному зворотному зв’язку провідність елементів, що його створюють, перераховується у вхідне коло шляхом домноження цієї провідності на величину 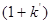. Саме це й зроблено на рис. 3.9, де елементи і 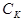перераховано у вхідне коло як

(3.29)

.

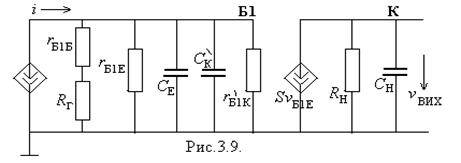
Тим самим ми виконали поставлену вище задачу, розділивши вхідне та вихідне кола . Тепер усі реактивні елементи (ємності 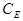та 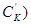, котрі характеризують наш транзистор, опинилися у вхідному колі, а всі реактивні елементи зовнішньої схеми (ємність 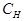) - у вихідному. Джерело вхідного сигналу замінено на рис.3.9 еквівалентним генератором струму з внутрішнім опором , де .

Тепер напругу 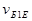, яка керує струмом у вихідному колі, можна визначити як

(3.30)

де . Звичайно одиницею порівняно з 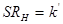можна нехтувати, отже, . Можна знехтувати також і величиною порівняно з 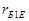, оскільки остання звичайно набагато менша від .

3.5.2. Коефіцієнт підсилення в області високих частот

Згідно з (3.27) вихідна напруга дорівнює 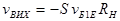. Ємність 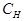вважатимемо поки що рівною нулеві. Підставивши у вираз для значення з формули (3.30), дістанемо

(3.31)

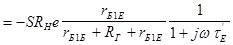
де 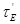- ефективна стала часу у схемі підсилювача:

(3.32)

Коефіцієнт підсилення каскаду 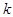визначається відношенням 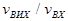, де вхідна, тобто базово - емітерна , напруга згідно (3.26) дорівнює

.

Врахувавши наведені вище притаманні схемі Джіоколетто співвідношення 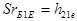, 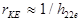та , дістанемо для коефіцієнта підсилення вираз

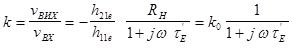(3.33)

де - одержан6ий нами раніше коефіцієнт підсилення каскаду в області середніх частот (3.6). Вираз (3.33) відрізняється від (3.6) співмножником, що описує частотну залежність коефіцієнта підсилення, яка виявляється подібною до частотної залежності, одержаної вище для підсилювача на польовому транзисторі (2.3). отже, при відсутності ємності у вихідному колі ( , верхні гранична частота, на якій підсилення каскаду становитиме , буде дорівнювати .

Якщо ж врахувати наявність ємності 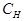, то замість 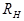в формулу (3.33) слід підставити повний опір навантаження, який тепер становитиме

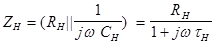де (3.34)

Отже, загальний коефіцієнт підсилення каскаду є

У першому наближення постійні часу можна об’єднати і звести одержаний вираз до вигляду

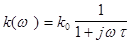(3.35)

де загальна стала часу підсилювального каскаду; вона дорівнює сумі сталих часу транзистора і навантаження. Верхня гранична частота каскаду тепер дорівнюватиме , а вигляд АЧХ та ФЧХ буде такий самий, як це зображено на рис.2.10 для підсилювача на польовому транзисторі.

3.5.3. Коефіцієнт підсилення в області низьких частот

Поведінка коефіцієнта підсилення в області низьких частот була докладно розглянута вище (п.2.3) для каскаду на польовому транзисторі. Тому ми обмежимося тут лише коротким повторенням викладеного вище стосовно до підсилювального каскаду на біполярному транзисторі, схема якого була дана на рис. 3.5.

В області низьких частот коефіцієнт підсилення подібного підсилювача знижується через наявність на його вході розділової ємності , яка разом із вхідним опором каскаду 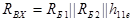утворює подільник. Він поділяє вхідну напругу в 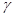разів де

.

Загальний коефіцієнт підсилення буде тепер у 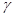разів меншим від «чистого» коефіцієнта підсилення . Таким чином, модуль коефіцієнта підсилення дорівнюватиме

(3.36)

де 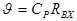- стала часу вхідного кола каскаду. Нижньою граничною частотою слід вважати . На цій частоті коефіцієнт підсилення знижується в разів порівняно з - коефіцієнтом підсилення на середніх частотах .

Оскільки вхідний опір біполярного транзистора звичайно невеликий, то для успішної роботи каскаду аж до досить низьких частот, розділову ємність доводиться робити достатньо великою, порядку десятків, а то й сотень мікрофарад.

3.5.4. Корекція частотної характеристики

Невеличкими ускладненнями схеми можна дещо поліпшити АЧХ підсилювача з рахунок підняття його верхньої граничної частоти 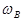та зниження нижньої граничної частоти .

Зменшення коефіцієнта підсилення підсилювача на біполярному транзисторі в області високих частот обумовлене значною мірою зменшенням параметру 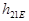. «Завал» АЧХ, який при цьому утворюється, можна, в принципі, компенсувати, застосовуючи як навантажувальний опір послідовно сполучені резистор та індуктивність (рис.3.10).

Повний опір навантаження 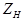тоді дорівнюватиме:

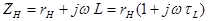, де (3.37)

Підставивши 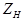у (3.33), дістанемо

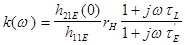(3.38)

де - значення цього параметра в області достатньо низьких частот[1]. При оптимальному підборі індуктивності, коли виконується умова , частотно - залежні члени в (3.38) скорочуються і коефіцієнт підсилення виявляється незалежним від частоти. Якщо ж індуктивність більша за оптимальну, то повинне спостерігатися навіть зростання коефіцієнта підсилення (рис.3.11, крива 3).

В дійсності згодом почне давати взнаки паразитна ємність , яка шунтує вихід підсилювача. На жаль, вплив не може бути скомпенсованим нарощуванням повного опору у колі колектора. Тому на достатньо високих частотах всі АЧХ для будь - яких значень зазнають спадання. Оптимальним вважається те значення індуктивності, при якому амплітудно - частотна характеристика, залишаючись монотонною забезпечує найбільше значення верхньої граничної частоти.

Корекція в області низьких частот здійснюється тим же шляхом, як і у підсилювачах на польових транзисторах.

[1] Вихідною провідністю 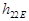та паразитною ємністю поки що нехтуємо.