Застосування генетичних алгоритмів

Розглянемо використання ГА на прикладі задачі комівояжера для 20 міст. Як особини (індивідууми) розглядатимемо маршрути обходу. Інформацію про маршрут можна записати у вигляді однієї хромосоми - вектора довжини 20, де в першій позиції стоїть номер першого міста на шляху проходження, потім - номер другого міста і т.д. Перше утруднення виникає, коли ми намагаємося визначити мутації для таких хромосом - стандартна операція, що змінює тільки одну позицію вектора, недопустима, оскільки приводить до некоректного маршруту. Але можна визначити мутацію як перестановку значень двох випадково вибраних генів. При такому перетворенні шлях проходження міняється тільки в двох містах.

За умовою задачі в даних хромосомах кожен ген (номер міста) повинен зустрічатися тільки один раз. Такий різновид хромосом називається хромосоми " з унікальними генами" і часто використовується в комбінаторних задачах. Стандартна операція схрещування для цього типу хромосом знову ж таки некоректна, тому тут використовується складніша схема двоточкового схрещування.

В процесі еволюції довжина найкоротшого маршруту в популяції монотонно зменшується до деякого моменту, а потім стабілізується. Знайдений маршрут, ймовірно, не є найоптимальнішим, але близький до нього по довжині - як правило, генетичні алгоритми "помиляються" не більше ніж на 5-10%. Цей недолік компенсується для комбінаторних задач відносно високою швидкістю роботи На практиці генетичні алгоритми нерідко використовують спільно з іншими методами, які дозволяють підвищити їх точність.

Генетичні алгоритми використовуються не тільки в задачах комбінаторного типу (як TSP), але і в тих випадках, коли підбирані параметри можуть бути будь-якими дійсними числами. Така, наприклад, задача оптимального розподілу інвестицій.

Генетичні алгоритми є евристичним підходом, тобто показує добрі результати на практиці, але погано піддається теоретичному дослідженню і обгрунтуванню. Ця популярність викликана, мабуть, винятковою красою підходу і його близькістю до природного механізму.

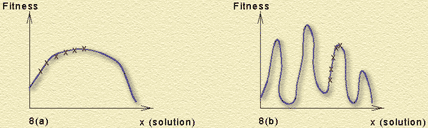
Рис.3. Знаходження оптимального рішення (a) и локального максимума (b) методом ітерацій.

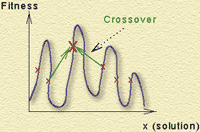
Рис. 4. Генетический пошук.

Для багатьох задач метод перебору потребую дуже багато часу, а градієнтний метод не гарантує знаходження глобального екстремуму. Проте, комбінуючи перебірний і градієнтний методи, можна сподіватися одержати хоча б наближене рішення, точність якого зростатиме при збільшенні часу розрахунку.

Генетичний алгоритм є саме таким комбінованим методом. Механізми схрещування і мутації в якомусь значенні реалізують переборну частину методу, а відбір кращих рішень - градієнтний спуск. Така комбінація дозволяє забезпечити стійко хорошу ефективність генетичного пошуку для будь-яких типів задач.