Проходження сигналів у нелінійних електричних колах

Ми вже мали можливість упевнитися в тому, що при проходженні гармонічного сигналу через нелінійний елемент електричного кола форма сигналу зазнає зміни. Зберігаючи періодичність з періодом , він перестає бути синусоїдальним. Подібне спотворення форми можна описати як появу у сигналі вищих гармонічних складових (гармонік) з частотами

Якщо сигнал складається не з одної, а з декількох гармонічних складових (наприклад, з двох з частотами 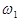і 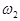), то комплект частот, тобто спектр сигналу, по проходженню через нелінійний елемент вельми збагачується і ускладнюється. У його складі будуть тепер присутні не тільки вищі гармоніки вхідних сигналів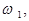 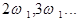і 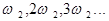, але і їх комбінаційні складові , де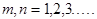

Ці процеси широко застосовуються для перетворення спектрів в системах радіозв’язку і тому раніш ніж розпочати розгляд принципів роботи радіопередавальних та радіоприймальних пристроїв слід ознайомитись з питаннями проходження складних сигналів у нелінійних електричних колах.

Розглянемо докладніше процес проходження через нелінійний чотириполюсник двох гармонічних сигналів з частотами 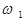і (рис.1). Нехай до входу чотириполюсника прикладена змінна напруга

(1)

а також постійна напруга (рис.1). Струм на виході чотириполюсника є функцією сумарної напруги :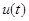

, (2)

де вигляд функції 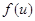визначається прохідною характеристикою нашого чотириполюсника. Будемо вважати, що змінна складова напруги 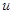набагато менша від її постійної складової

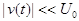. (3)

Тоді можна скористатися розкладом функції 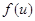у ряд Тейлора в околі робочої точки .

(4)

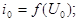
де [1].

За своїм фізичним змістом величина є крутість прохідної характеристики в околі робочої точки. Що ж до величини , то вона пропорційна до кривини функції 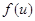в околі робочої точки і надалі ми будемо називати величину просто кривиною. Ці величини можна наближено визначити по трьох точках в околі точки О (рис.2):

Підставивши (1) в (4), одержуємо

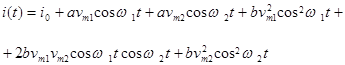
(5)

і використовуючи відомі формули тригонометрії

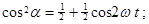
одержуємо

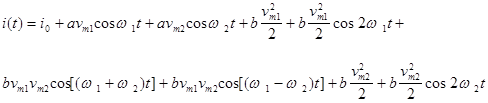(6)

Як видно, окрім початкових частот 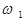і , у спектрі струму з’явилися другі гармоніки 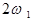і , а також комбінаційні частоти та . Постійна складова струму збільшилася на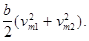

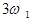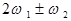Врахування кубічного члену ряду (4) призвело б до появи складових з частотами і , а також нових комбінаційних частот і 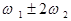та деякої зміни амплітуд перших гармонік 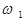і .