Относительность длин и промежутков времени.

1. Ввести понятие Лоренцева сокращения?

2. Вывести формулу для Лоренцева сокращения?

3. Какие линейны е размеры называют собственными?

4. Что означает относительность линейных размеров тел?

5. Какое время называют собственным?

6. Вывести формулу для преобразования промежутков времени?

7. Что означает релятивистское замедление времени?

1. Из преобразований Лоренца следует, что линейный размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении движения. Это изменение продольного размера тела при его движении называют ЛОРЕНЦЕВЫМ СОКРАЩЕНИЕМ.

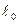Пусть -длина стержня, покоящегося в системе отсчета К`.

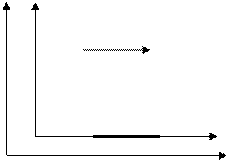
Y Y`

K K`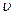

x₁ x₂ X`

O` X

O x₁(t) x₂(t)

Если стержень расположен вдоль оси O`X`, то 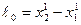, х₁` и x<sub>2</sub>` - координаты концов стержня.

Поскольку стержень движется, нужно произвести одновременный отсчет коордтнат его концов х₁` и x<sub>2</sub>` в некоторый момент времени t. Разность координат дает длину стержня в системе К.

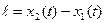
Для сопоставления длин возьмем формулу преобразований Лоренца, которая свяжет координаты x,x` и время t системы.

7. Закономерность, рассмотренная ниже в пункте 6 свидетельствует о существовании релятивистского эффекта замедления хода времени в движущейся ИСО по сравнению с неподвижной. Часы, движущиеся со скоростью 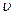относительно данной ИСО, идут медленнее в 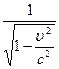раз, чем неподвижные; следовательно, в согласии с принципом относительности, все физические процессы в движущейся системе отсчета протекают медленнее, чем в неподвижной. Эффект замедления хода становится заметным только при очень больших скоростях движения 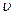, близких к скорости света в вакууме.

К 4.3

Формула (4.28) представляет собой не только формулу преобразования скорости при переходе от одной СО к другой, но, также и формулу сложения скоростей в релятивистской динамике. Причем, структура этой формулы такова, что даже в том случае, когда два тела движутся навстречу друг другу со скоростью, равной скорости света, все равно скорость их относительного движения будет равна не 2С, а просто С.

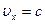
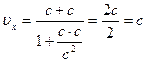
Это говорит о том, что формула релятивистского сложения скоростей согласуется со вторым постулатом теории относительности.

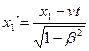
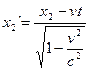
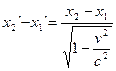
Заменив разности координат длинами стержня, а относительную скорость 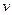систем К и К`, равной ей скоростью стержня 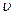, с которой он движется в системе К, придем к формуле:

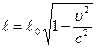
5. Время, измеряемое по часам, движущимся вместе с данным объектом называют СОБСТВЕННЫМ ВРЕМЕНЕМ.

6. Пусть в движущейся ИСО К` два рассматриваемых события 1 и 2 происходят в одной и той же неподвижной относительно K` точке А(х₂`=х<sub>1</sub>`) в моменты времени t₁ и t₂, так, что промежуток времени между этими событиями 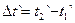относительно неподвижной ИСО К.

Точка А движется с той же скоростью 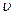, что и система К`. Поэтому в К события 1 и 2 совершаются в разных точках пространства с координатами х₁ и х₂ = 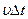, где 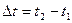- промежуток времени между событиями 1 и 2 по часам в системе отсчета К. Из преобразований Лоренца следует, что: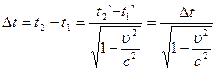

Рассмотрим каким образом преобразуется скорость движения точки при переходе от одной ИСО к другой. Нештрихованной системе скорость 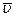может быть записана:

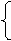
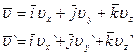(4.22)

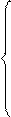
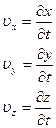(4.23)

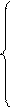
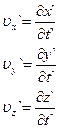(4.24)

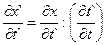(4.25)

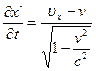(4.26)

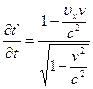(4.27)

Подставим (4.27) в (4.25):

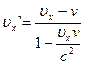(4.28)

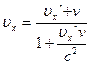
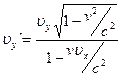
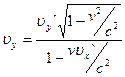
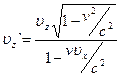
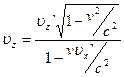
Эти формулы выражают закон сложения скорости в релятивистской кинематике.

При помощи аналогичной процедуры можно вывести формулу, которая будет связывать ускорение в штрихованной и нештрихованной системах отсчета.

Ускорение в штрихованной СО находится по формуле:

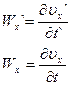(4.29)

Перепишем правую часть первой из формул в виде:

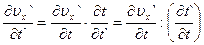(4.30)

Первый сомножитель в этой формуле можно найти используя связь между 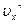и :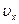

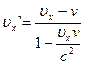
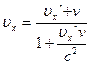
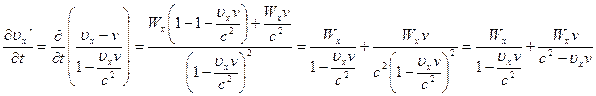(4.31)

Релятивистская динамика. Уравнение движения релятивистской частицы. Инвариантность уравнения движения относительно преобразований Лоренца.

Если математическое уравнение выражающее некоторый физический закон не меняет своего вида при переходе от одной системы отсчета к другой, от говорят, что этот закон КОВАРИАНТЕН относительно преобразований координат Лоренца.