Соединение в звезду
На рис. 6 приведена трехфазная система при соединении фаз генератора и нагрузки в звезду. Здесь провода АА’, ВВ’ и СС’ – линейные провода.

Линейнымназывается провод, соединяющий начала фаз обмотки генератора и приемника. Точка, в которой концы фаз соединяются в общий узел, называется нейтральной(на рис. 6 N и N’ – соответственно нейтральные точки генератора и нагрузки).
Провод, соединяющий нейтральные точки генератора и приемника, называется нейтральным(на рис. 6 показан пунктиром). Трехфазная система при соединении в звезду без нейтрального провода называется трехпроводной,с нейтральным проводом – четырехпроводной.
Все величины, относящиеся к фазам, носят название фазных переменных,к линии - линейных.Как видно из схемы на рис. 6, при соединении в звезду линейные токи 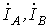 и
и 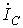 равны соответствующим фазным токам. При наличии нейтрального провода ток в нейтральном проводе
равны соответствующим фазным токам. При наличии нейтрального провода ток в нейтральном проводе  . Если система фазных токов симметрична, то
. Если система фазных токов симметрична, то  . Следовательно, если бы симметрия токов была гарантирована, то нейтральный провод был бы не нужен. Как будет показано далее, нейтральный провод обеспечивает поддержание симметрии напряжений на нагрузке при несимметрии самой нагрузки.
. Следовательно, если бы симметрия токов была гарантирована, то нейтральный провод был бы не нужен. Как будет показано далее, нейтральный провод обеспечивает поддержание симметрии напряжений на нагрузке при несимметрии самой нагрузки.
Поскольку напряжение на источнике противоположно направлению его ЭДС, фазные напряжения генератора (см. рис. 6) действуют от точек А,В и С к нейтральной точке N; 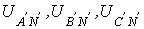 - фазные напряжения нагрузки.
- фазные напряжения нагрузки.
Линейные напряжения действуют между линейными проводами. В соответствии со вторым законом Кирхгофа для линейных напряжений можно записать
 ; ;
| (1) |
 ; ;
| (2) |
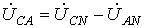 . .
| (3) |
Отметим, что всегда  - как сумма напряжений по замкнутому контуру.
- как сумма напряжений по замкнутому контуру.
На рис. 7 представлена векторная диаграмма для симметричной системы напряжений. 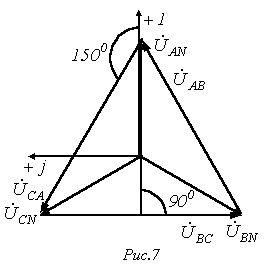
Как показывает ее анализ (лучи фазных напряжений образуют стороны равнобедренных треугольников с углами при основании, равными 300), в этом случае

| (4) |
Обычно при расчетах принимается  . Тогда для случая прямого чередования фаз
. Тогда для случая прямого чередования фаз  ,
,  (при обратном чередовании фазфазовые сдвиги у
(при обратном чередовании фазфазовые сдвиги у  и
и  меняются местами). С учетом этого на основании соотношений (1) …(3) могут быть определены комплексы линейных напряжений. Однако при симметрии напряжений эти величины легко определяются непосредственно из векторной диаграммы на рис. 7. Направляя вещественную ось системы координат по вектору
меняются местами). С учетом этого на основании соотношений (1) …(3) могут быть определены комплексы линейных напряжений. Однако при симметрии напряжений эти величины легко определяются непосредственно из векторной диаграммы на рис. 7. Направляя вещественную ось системы координат по вектору 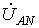 (его начальная фаза равна нулю), отсчитываем фазовые сдвиги линейных напряжений по отношению к этой оси, а их модули определяем в соответствии с (4). Так для линейных напряжений
(его начальная фаза равна нулю), отсчитываем фазовые сдвиги линейных напряжений по отношению к этой оси, а их модули определяем в соответствии с (4). Так для линейных напряжений 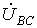 и
и  получаем:
получаем: 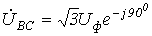 ;
;  .
.
Дата добавления: 2016-04-14; просмотров: 424;
