ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ УДЕЛЬНЫХ ТЕПЛОЕМКОСТЕЙ ГАЗОВ АДИАБАТИЧЕСКИМ МЕТОДОМ

Отношение количества теплоты dQ, сообщенной системе (телу), к соответствующему повышению температуры dT

С= ,

называют теплоемкостью. Теплоемкость, отнесенную к единице массы вещества, называют удельной, отнесенную к молю – молярной (мольной) теплоемкостью.. Единицы измерения теплоемкости: Дж / (кг^.К); Дж / (моль^.К).

Приведенное определение теплоемкости не является достаточным, так как количество теплоты dQ, сообщаемое телу, зависит от характера процесса, в результате которого тело переходит в новое состояние. Другими словами, необходимо еще указать условия, при которых производится нагревание. Эта неопределенность обусловлена тем, что количество теплоты не является функцией состояния тела в отличие, например, от внутренней энергии.

В связи с отмеченной неоднозначностью возможны различные определения теплоемкости. Так, для термодинамической системы, состояние которой определяется параметрами р,V и Т, вводят понятия теплоемкости при постоянном объеме С_V и теплоемкости при постоянном давлении С_р. Эти теплоемкости характеризуются количеством тепла, сообщаемым системе, в условиях, когда остается неизменным либо объем, либо давление.

Согласно первому началу термодинамики, выражающему закон сохранения энергии , теплота dQ, сообщаемая системе, затрачивается на увеличение внутренней энергии системы dU и на работу dA, которую система совершает над внешней средой. Первое начало выражается соотношением

dQ=dU+dA

(Более строго это соотношение записывается так: dQ=dU+dA, чтобы подчеркнуть то обстоятельство, что только dU является полным дифференциалом, поскольку среди величин Q,U и А только U является функцией состояния системы).Работа при отсутствии магнитных и электрических явлений связана только с изменением объема газа и равна dA=p ^. dV . Таким образом, dQ=dU+pdV.

Если нагревание происходит при постоянном объеме (dV=0), то все тепло тратится на увеличение внутренней энергии:

dQ=dU .

Отсюда вытекает, что

С_V=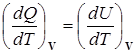

Так как для идеального газа внутренняя энергия является только функцией температуры: U=U(T), то можно записать

С_V= .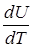

Для изобарического процесса (р=const)

C_p= .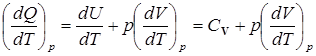

В соответствии с уравнением состояния одного моля идеального газа

V= ,

где R – универсальная газовая постоянная, равная 8,31 Дж/ (моль^. К) (R – численно равна работе, которую совершает один моль газа при изменении его температуры на один градус при постоянном давлении), при р=const находим

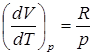
и для С_р имеем С_р=С_V+R.

Это уравнение называется уравнением Майера. Теплоемкость С_р всегда больше теплоемкости С_V (С_р>C_V). Это неравенство носит общий характер и справедливо не только для газов, где превышение С_р над С_V связано с работой, совершаемой газом при расширении (при р=const), но и для тех «исключительных» тел, объем которых уменьшается при нагревании, например, для резины.

При описании некоторых физических явлений приходится иметь дело с отношением удельных теплоемкостей, которое обозначим g= 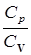. Одним из таких процессов, играющих важную роль при изучении тепловых явлений, является адиабатический процесс. Этот процесс протекает без теплообмена с внешней средой. Значит, работа, совершаемая системой в этом случае, производится за счет изменения ее внутренней энергии.

Из первого начала термодинамики для адиабатического процесса (dQ=0) имеем

dU+pdV=0

Для идеального газа dU=C_VdT, отсюда для термически изолированной системы

С_VdT+ pdV=0.

(1)

Из уравнения рV=RT простым дифференцированием получаем

рdV+Vdp=RdT; dT=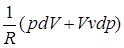

(2)

Введя (2) в уравнение (1), имеем

;

(C_V+R)pdV+C_VVdp=0;

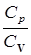
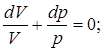g

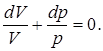
Интегрируя, получаем

g lnV+ln p=const,

откуда pV ^g=const и

TV ^g-1= const.

Соотношения pV ^g=const, TV ^g-1=const иногда называют уравнением Пуассона.

В молекулярно-кинетической теории газ рассматривается как совокупность свободно движущихся частиц, подчиняющихся законам классической механики. Эта теория позволяет удовлетворительно объяснить некоторые основные свойства реальных газов, в частности, дает возможность оценить порядок величин С_р, С_V и g.

Согласно представлениям кинетической теории, молекулы идеального газа не взаимодействуют между собой. Поэтому внутренняя энергия такого газа не зависит от изменения объема и давления и является функцией только температуры. Каждая частица одноатомного газа приближенно рассматривается как материальная точка. Так как материальная точка имеет три степени свободы, ее кинетическая энергия равна 1,5kT. Следовательно, в среднем на каждую степень свободы приходится энергия, равная 0,5кТ. Внутренняя энергия многоатомных газов складывается из кинетических энергий поступательного и вращательного движения молекул. Применяя в этом случае положение о равном распределении энергии по степеням свободы, можем подсчитать среднюю кинетическую энергию многоатомной молекулы:

w= ,

где i – число степеней свободы молекул; k – постоянная Больцмана.

Внутреннюю энергию одного моля газа найдем, умножив эту энергию на число молекул в одном моле:

U₀= ,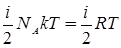

где N_А– число Авогадро.

Продифференцировав внутреннюю энергию по температуре, получим молярную теплоемкость газа при постоянном объеме:

С_V= .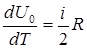

В работе требуется найти отношение удельных теплоемкостей воздуха. Поскольку воздух состоит в основном из смеси двухатомных газов (водорода, кислорода, азота) и каждой молекуле приписывают пять степеней свободы, то отношение теплоемкостей для воздуха будет равно g=1,40. Это довольно хорошо согласуется с экспериментальными данными, полученными для чистого воздуха, свободного от СО₂ и паров воды при нормальных условиях.

ОПИСАНИЕ УСТАНОВКИ И ВЫВОД РАБОЧЕЙ ФОРМУЛЫ

Величину С_р экспериментально можно найти обычным калориметрическим способом, но определение С_V на опыте связано со значительными трудностями; вследствие этого представляется более удобным, найдя предварительно величину С_р, вычислить С_V по известным С_р и g.

Идея опыта заключается в следующем: допустим, что некоторая масса газа m характеризуется начальным состоянием I: объемом V₀; давлением р₀+h и температурой Т₀. Заставим газ быстро расширяться. Кратковременность процесса позволяет пренебрегать теплообменом с окружающей средой, т.е. процесс считать адиабатическим. В конце процесса расширения газ перейдет в состояние II, характеризующееся объемом V₁>V₀; давлением р₀ и температурой Т₁<Т₀. Предоставим газу нагреваться при постоянном объеме до прежней температуры Т₀, которая равна температуре окружающей среды. В конце этого процесса состояние III газа будет характеризоваться прежним объемом V₁, давлением р₀+h₁, и температурой Т₀. При адиабатическом процессе перехода газа из состояния I в состояние II будет выполняться условие

р₀ V₀^g=(р₀+h) V₀^g

(3)

Cостояния I и III характеризуются одинаковой температурой, следовательно, переход массы газа m из состояния I в состояние III можно осуществить и по изотерме, т.е.

(р₀+h)V₀=(p₀+h₁)V₁

(4)

Равенства (3) и (4) можно переписать в виде

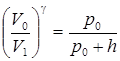и .

Отсюда

.

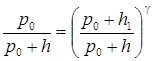Логарифмируя, получаем

ln .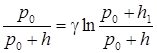

Отсюда определяем g=

Разлагая логарифмы в ряды по формуле

ln(1-x)=-x+ 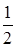x²- 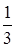x³+…. и ограничиваясь только первыми членами, найдем приближенное выражение

g= . (5)

Таким образом, можем для определения величины g ограничиться наблюдением над изменениями давления газа ,т.е. величин h и h₁.

Из уравнения Майера и выражения (5), находим

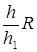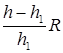С_р= ; C_V= (6)

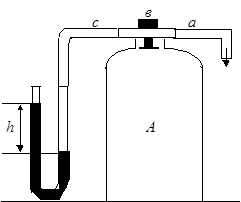
Для проведения опыта служит прибор Клемана-Дезорма , состоящий из большого стеклянного баллона А, в горловину которого вставлена пробка, залитая для герметизации замазкой; через пробку проходит латунная трубка, имеющая два отвода: одно из них а соединен с насосом, служащим для накачивания воздуха в сосуд, другой с связан с манометром. Сверху пробка имеет клапан в для выпуска воздуха.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ОБРАБОТКИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ

Опыт производится следующим образом: накачивают в сосуд А воздух до давления h=2000…3000 Па (200-300мм водяного столба по манометру) и закрывают зажим на резиновом шланге. Через некоторое время, когда разность уровней манометрической жидкости установится примерно постоянной, производят отсчет давления по манометру (h). Затем нажимают на кнопку, тем самым дают возможность газу рашириться, и через очень короткий промежуток времени (2-3 секунды) кнопку отпускают. Таким образом осуществляется адиабатический процесс перехода газа из состояния I в состояние II. Так как при адиабатическом процессе газ в баллоне сообщается с окружающим воздухом, то, очевидно, давление его падает до атмосферного р₀ и, вместе с тем, понижается темпратура газа. После того как кнопку отпускают, предоставленный самому себе газ начинает нагреваться за счет теплоты окружающей среды, и его давление, наблюдаемое по манометру, растет. Замечают момент, когда показание манометра достигает максимума, и производят отсчет h₁.

По полученным величинам h и h₁ можно вычислить g, С_р, С_V.

В компьютерном варианте данная лабораторная работа выполняется в следующем порядке.

1.Начертить в тетради таблицу 1.

Таб. 1

№ опыта	h, мм вод. ст.	h1, мм вод. ст.

2. Включить компьютер.

3.Запустить программу 8К.ЕХЕ. Для этого указать курсором на 8К.ЕХЕ и щелкнуть левой кнопкой мышки (в дальнейшем эту команду обозначим L’ на 8К.ЕХЕ). Изучить информацию на экране.

4. L’ на команде начать.

5. L’на насос.

6. L’ на кнопку клапана. Один опыт завершен.

7. L’ на прдолжить.

8. Повторить пункты5-7 еще 3 раза.

9. Повторить пункты5-6 еще 1 раз.

10.Переписать все данные таблицы в тетрадь. _.

11. L’ на выход.

12. Вычислить C_p, C_v, g.

13. Вычислить средние значения и погрешности величин C_p, C_v, g.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Сформулируйте определение теплоемкости.

2. Чем характеризуются теплоемкости С_р и С_V?

3. Cформулируйте первое начало термодинамики и напишите его применительно к изопроцессам.

4. Выведите соотношение, связывающее теплоемкости С_р и С_V.

5. В чем заключается физический смысл универсальной газовой постоянной?

6. Какой процесс называется адиабатическим?

7. Как записывается уравнение Пуассона? Приведите вывод этого уравнения.

8. Как определяются молярные теплоемкости?

9. Что такое число степеней свободы молекул?

10. В чем заключается идея опыта?

11. Почему при адиабатическом расширении газа температура уменьшается?

12. Приведите вывод рабочей формулы.