Зависимость газодинамических параметров от числа Маха. Газодинамические функции
Число Маха это отношение скорости к скорости звука:
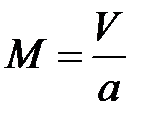 .
.
Запишем уравнение энергии в виде:
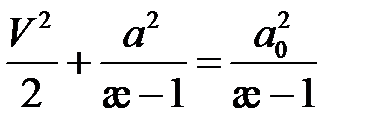 ,
,
разделим левую и правую часть на 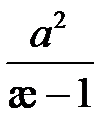 :
:
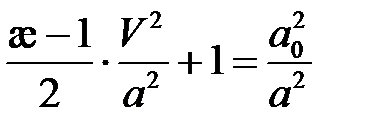 .
.
Т.к. 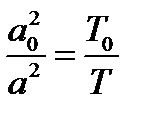 , а
, а 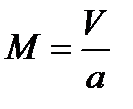 , имеем:
, имеем:
 ,
,
соответственно:
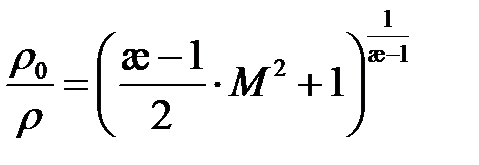 ,
,
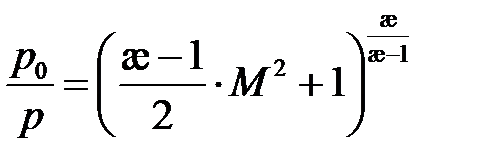 .
.
Таким образом:
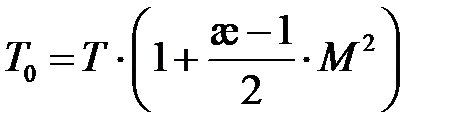
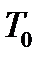 - температура соответствующая заторможенному потоку (
- температура соответствующая заторможенному потоку ( 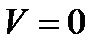 ).
).
Эта формула показывает, что температура при росте числа Маха М, в той точке, где поток затормозится, может достигать значительных величин.
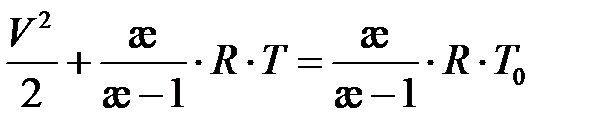 ,
,
перепишем это выражение в виде:
 , где
, где 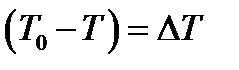 - изменение температуры.
- изменение температуры.
 .
.
Выразим изменение температуры  .
.
 .
.
Подставляя в формулу различные значения скорости полёта аппарата, получим соответствующие значения изменения температуры:
V=240 м/с DТ=28,6 градусов. Соответствует полету с М=0,8.
V=600 м/с DТ=179 градусов. Соответствует полету с М=2.
V=2500 м/с DТ=3111 градусов. Соответствует участку максимальных тепловых нагрузок спускаемого аппарата в плотных слоях атмосферы.

|
При заданных значениях параметров аппарат, проходя через атмосферу, нагрелся на 3111 градусjd.
Газодинамические функции записываются в обратном виде:
 ,
,
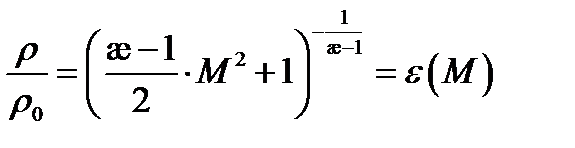 ,
,
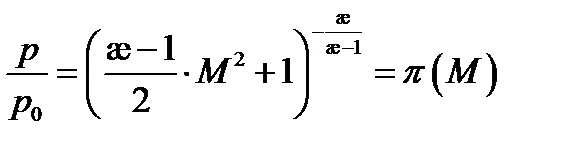 .
.
Пусть  - число Маха
- число Маха 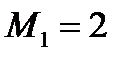 , требуется найти
, требуется найти 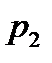 для
для  .
.
Найдем отношение  :
:
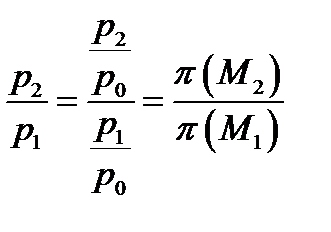 . Пользуясь таблицей, находим неизвестное значение
. Пользуясь таблицей, находим неизвестное значение 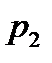 .
.
При составлении таблицы существует неудобство, т.к. значения 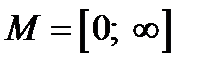 .
.
 .
.
Приведенная скорость (коэффициент скорости)
 - приведенная скорость (коэффициент скорости).
- приведенная скорость (коэффициент скорости).
Получим связь между  и
и 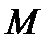 . Запишем уравнение энергии:
. Запишем уравнение энергии:
 ,
,
преобразуем первый член и перепишем в виде:
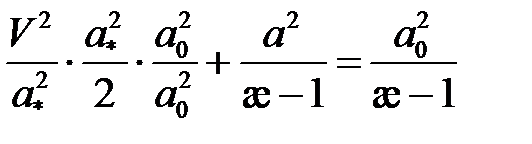 ,
,
разделим левую и правую часть на  :
:
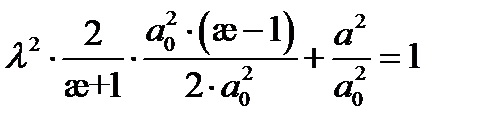 ,
,
Учитываем, что
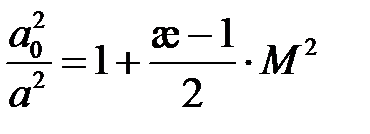 ,
,
получим
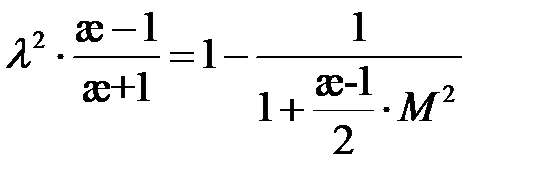 ,
,
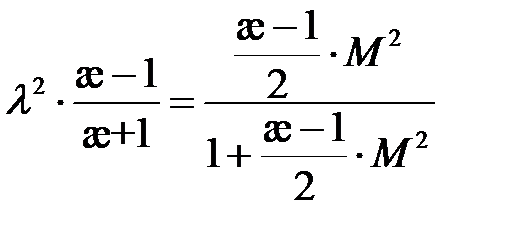 ,
,
Окончательно получим связь между коэффициентом скорости и числом Маха
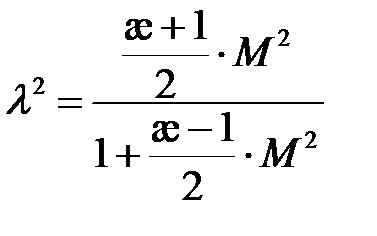 .
.
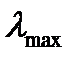 соответствует
соответствует 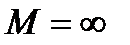 , тогда:
, тогда:
 ,
,
раскрывая неопределимость при помощи правила Лапиталя, получим:
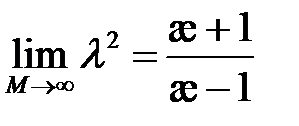 .
.
Для воздуха 
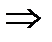
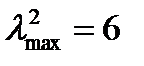 ,
, 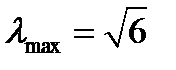 .
.
Сопло Лаваля
Запишем уравнение неразрывности для осесимметричного потока:

Продифференцируем это уравнение и разделим на  :
:
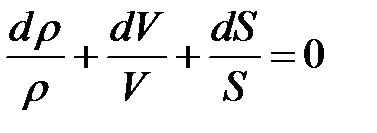
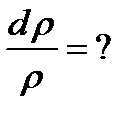
Скорость звука 

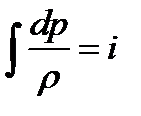
Дифференцируя уравнение энергии  , получим:
, получим:

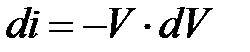
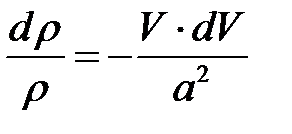
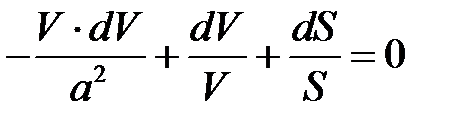
Получим уравнение (уравнение Гюгонио)
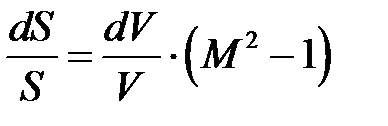
Если поток дозвуковой 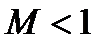 , то
, то
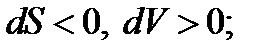
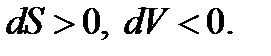
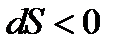
|
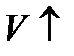
|

|

|
Если поток сверхзвуковой  , то
, то
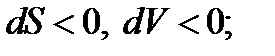

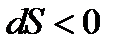
|

|

|
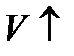
|
График изменения скорости по соплу:

Если 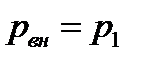 , то это повышенное давление должно проникнуть в сопло. Оно приводит к тому, что в сопле образуется прямой скачок уплотнения, на котором звуковая скорость будет падать и становится дозвуковой.
, то это повышенное давление должно проникнуть в сопло. Оно приводит к тому, что в сопле образуется прямой скачок уплотнения, на котором звуковая скорость будет падать и становится дозвуковой.
Замечание: сверхзвуковую скорость можно получить в цилиндрической трубе. Существует два принципиальных способа:
Можно добавлять газ по определенному закону, а потом отнимать газ по другому закону (расходное сопло)
| газ |
| газ |
| кр |
Можно нагревать и охлаждать трубу по определенному закону (тепловое сопло)
| тепло |
| кр |
| тепло |
Дата добавления: 2016-04-14; просмотров: 4649;
