Примеры решения задач. Определение перемещений в балках аналитическим способом

Определение перемещений в балках аналитическим способом

Пример 1

Условие задачи

Для балки, показанной на рис. 4.20, а, требуется найти прогиб в сечении С, угол поворота в сечении В аналитическим способом и проверить условие жесткости, если допускаемый прогиб равен l/100. Балка выполнена из дерева и имеет поперечное сечение из трех бревен радиусом 12 см. (Подбор сечения этой балки см. в разд. 4.1.2, пример 1.)

Решение

Для определения перемещений балки аналитическим способом составим дифференциальное уравнение изогнутой оси (4.16), используя правила Клебша записи выражения для изгибающего момента. Начало координат в рассматриваемой задаче рациональнее выбрать справа (в заделке). Распределенную нагрузку , которая не доходит до левого конца балки, продлим до сечения С (рис. 4.20, в). Выражение для изгибающего момента будет иметь такой вид:

.

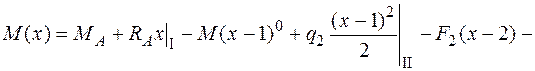
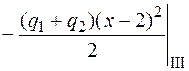Подставим это выражение в дифференциальное уравнение (4.16) и проинтегрируем его два раза:

;

;

.

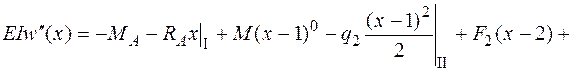
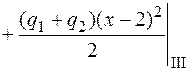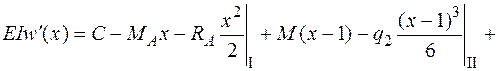
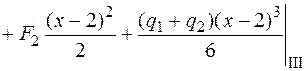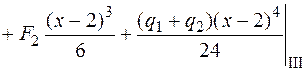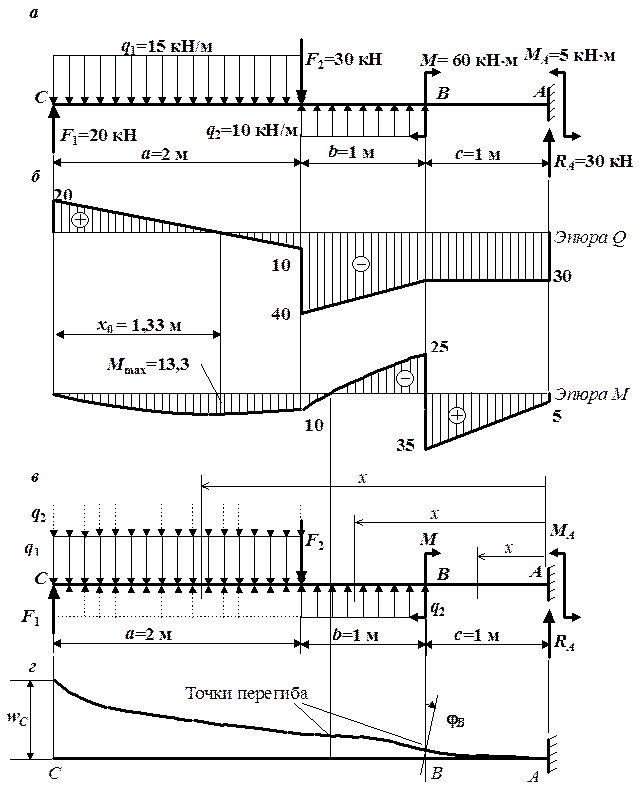Рис. 4.20. К решению примера 1 аналитическим способом: а – схема балки с нагрузками; б) эпюры Q и М; в – иллюстрация правил Клебша; г – изогнутая ось балки

Для определения постоянных С и D запишем граничные условия: в заделке (в сечении А, где находится начало координат) угол поворота и прогиб балки равны нулю, то есть

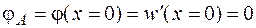и .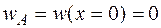

Подставляя эти условия в выражения для угла поворота и прогиба на первом участке, найдем, что

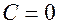и .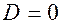

Теперь можно определить заданные перемещения. Для определения угла поворота в сечении В подставим в выражение для угла поворота на первом участке (только до черты с номером I) значение :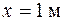

кН×м².

В соответствии с правилом знаков отрицательный знак угла поворота для выбранного начала координат х справа означает, что поворот сечения происходит по часовой стрелке.

В сечении С, где требуется найти прогиб, координата х равна 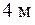, и это сечение находится на третьем участке балки, поэтому подставляем х = 4 м в выражение для прогибов, используя слагаемые на всех трех участках:

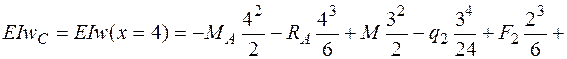
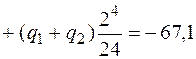кН·м³.

Знак минус у найденного прогиба показывает, что сечение С перемещается вверх. Покажем найденные перемещения на изогнутой оси балки. Чтобы нарисовать ось балки после деформации, построим эпюру изгибающих моментов (рис. 4.20, б). Положительный знак эпюры М на участке показывает, что балка на этом участке изгибается выпуклостью вниз, при отрицательном знаке М изогнутая ось имеет выпуклость вверх. Кроме того, деформированная ось балки должна удовлетворять условиям закрепления: в нашем случае на правом конце балка имеет жесткое защемление, и, как уже отмечалось при записи граничных условий, прогиб и угол поворота в защемлении должны равняться нулю. На рис. 4.20, г изображена ось рассматриваемой балки после деформации, удовлетворяющая этим условиям. На изогнутой оси показаны найденные прогиб в сечении С и угол поворота сечения В с учетом их знаков.

В заключение сосчитаем прогиб балки в сантиметрах, угол поворота в радианах и проверим условие жесткости. Найдем жесткость ЕI рассматриваемой деревянной балки из трех бревен радиусом 12 см. Момент инерции поперечного сечения

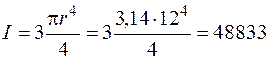см⁴.

Модуль упругости дерева Е = 10⁴ МПа = 10³ кН / см². Тогда

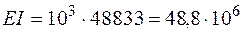кН·см².

Прогиб балки в сечении С

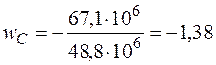см,

а угол поворота сечения В

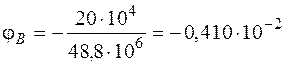рад.

Очевидно (см. рис. 4.20, г), что найденный прогиб балки в сечении С является максимальным, поэтому для проверки условия жесткости сравним его с допускаемым прогибом. Для балки длиной 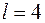м допускаемый прогиб согласно условию 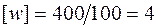см. Таким образом, максимальный прогиб 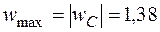см меньше допускаемого, и условие жесткости выполняется.

Пример 2

Условие задачи

В балке с двумя консолями, показанной на рис. 4.21, а надо найти угол поворота сечения А и прогиб сечения D, используя аналитический способ. Сечение балки – двутавр № 24.

Решение

Выберем начало отсчета координаты х на левом конце балки в точке А и запишем выражение для изгибающего момента на всех участках с учетом правил Клебша :

.

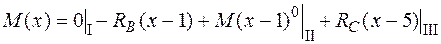Подставим это выражение в дифференциальное уравнение изогнутой оси (4.16) и проинтегрируем его дважды:

Рис. 4.21. К решению примера 2 аналитическим способом: а – схема балки с нагрузками; б – эпюры внутренних усилий; в – изогнутая ось балки

;

.

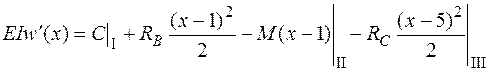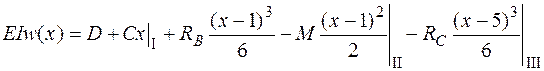Найдем произвольные постоянные С и D из граничных условий. В точках В и С, где находятся опоры, прогибы не возможны. Поэтому

,

.

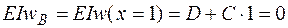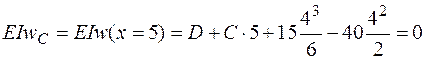Получили систему из двух уравнений с двумя неизвестными С и D. Решая эту систему, найдем С = 40 кН·м², D = – 40 кН·м³. Проанализируем результат, используя геометрический смысл произвольных постоянных С и D. На рис. 4.21, в показана изогнутая ось балки, соответствующая эпюре изгибающих моментов и условиям закрепления. Точка А, находящаяся в начале координат, перемещается вверх, и поэтому следует ожидать, что будет иметь в соответствии с правилом знаков отрицательный знак. Сечение в точке А поворачивается по часовой стрелке, поэтому постоянная 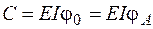должна быть положительна. Полученные знаки С и D не противоречат проведенному анализу.

Теперь можно найти искомые перемещения. Угол поворота сечения А определим, подставив в выражение для 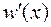на первом участке значение х = 0, то есть

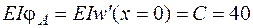кН·м².

Чтобы найти прогиб в точке D, в выражение для прогибов 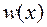подставляем 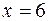м, используя все слагаемые этого выражения, так как точка находится на последнем третьем участке:

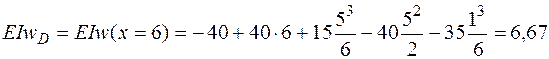кН·м³.

Разделим полученные результаты на жесткость балки, чтобы сосчитать угол поворота в радианах, а прогиб в сантиметрах. Жесткость стальной двутавровой балки № 24:

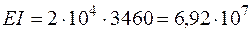кН·см².

Угол поворота сечения А

рад.

Прогиб точки D

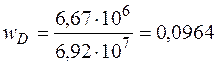см.

Положительные знаки полученных перемещений свидетельствуют о том, что поворот сечения А происходит по часовой стрелке, а точка D перемещается вниз. Изогнутая ось балки с найденными перемещениями и точкой перегиба показана на рис. 4.21, в.