Экономико-математическое моделирование.
Применение математике в экономике принимает форму экономико-математического моделирования. С помощью него изображается тот или иной действительный экономический процесс.
Моделирование– это один из важнейших методов научного познания, с помощью которого создается модель (условный образ) объекта исследования. Сущность его заключается в том, что взаимосвязь исследуемого показателя с факторными передается в форме конкретного математического выражения.
Моделирование факторных систем должно основываться на следующих экономических принципах:
· причинность;
· достаточная специфичность;
· самостоятельность существования;
· наличие учетной принадлежности.
Модель – условный образ объекта управления (исследования), она конструируется субъектом управления (исследования) так, чтобы отобразить характеристики объекта – свойства, взаимосвязи, структурные и функциональные параметры и т.п., существенные цели для управления (исследования)
В экономическом анализе используются математические модели, описывающие изучаемое явление или процесс с помощью уравнений, неравенств, функций и других математических средств. Различают математические модели с количественными характеристиками, записанными в виде формул; числовые модели с конкретными числовыми характеристиками; логические, записанные с помощью логических выражений, и графические, выраженные в графических образах. Модели, реализованные с помощью электронно-вычислительных машин, называют машинными, или электронными.
Экономико-математическая модель должна быть адекватной действительности, отражать существенные стороны и связи изучаемого объекта. Отметим принципиальные черты, характерные для построения экономико-математической модели любого вида.
Процесс моделирования можно условно подразделить на три этапа:
1) анализ теоретических закономерностей, свойственных изучаемому явлению или процессу, и эмпирических данных о его структуре и особенностях; на основе такого анализа формируются модели. Здесь необходима четкая формулировка конечной цели построения модели., а также определение критерия по которому будут сравниваться различные варианты решения. Такими критериями могут быть наибольшая прибыль или производительность труда.;
2) определение методов, с помощью которых можно решить задачу. Здесь необходимо выбрать наиболее рациональный математический метод для решения задачи;
3) анализ полученных результатов – всесторонний анализ результата, полученного при изучении экономического явления или процесса.
Окончательным критерием достоверности и качества модели являются практика, соответствие полученных результатов и выводов реальным условиям производства, экономическая содержательность полученных оценок. Если полученные результаты не соответствуют реальным производственным условиям, то необходим экономический анализ причин несоответствия. Такими причинами могут быть недостаточная достоверность информации. После того как причина определена, модель решается заново.
Таким образом, экономико-математическое моделирование работы предприятия должно быть основано на анализе его деятельности и, в свою очередь обогащать этот анализ результатами и выводами, полученными после решения соответствующих задач.
В экономическом анализе принято выделять следующие основные типы моделей:
дескриптивные – модели описательного характера, основанные на использовании информации, содержащейся прежде всего в бухгалтерской отчетности;
предикативные – модели предсказательного, прогностического характера, применяемые для прогнозирования доходов предприятия и его будущего финансового состояния;
нормативные – модели сравнения фактических результатов с ожидаемыми бюджетными.
В факторном анализе различают модели:
1. детерминированные (функциональные)
2. стохастические (корреляционные).
С помощью детерминированныхфакторных моделей исследуется функциональная связь между результативным показателем (функцией) и факторами (аргументами).
При создании детерминированных факторных моделей необходимо выполнять ряд требований:
1)факторы, включаемые в модель, должны реально существовать, а не быть надуманными абстрактными величинами или явлениями;
2)факторы, входящие в модель, должны находиться в причинно-следственной связи с изучаемым показателем.
3) все показатели факторной модели должны быть количественно измеримыми, т.е. иметь единицу измерения и необходимую информационную базу;
4) факторная модель должна обеспечивать возможность измерения влияния отдельных факторов, т.е. в ней должна учитываться соразмерность изменений результативного и факторных показателей, а сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.
В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.
1. Аддитивные модели:
Y = ∑ xi =х1+х2+... + хп
Они используются в тех случаях, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.
2. Мультипликативные модели:
Y =Пxi = x1*x2*x3…..xn
Этот тип моделей применяется в том случае, когда результативный показатель представляет собой произведение нескольких факторных показателей.
3. Кратные модели:
Y=X1/X2
Они применяются в том случае, когда результативный показатель получают делением одного факторного показателя на величину другого.
4. Смешанные (комбинированные) модели – сочетание в различных комбинациях предыдущих моделей:
Y =( a+b)/c, Y = a/(d+c), Y = a*b/c, Y = (a + b)cи т.д.
Применительно к классу детерминированных факторных систем различают следующие основные приемы моделирования:
1. Метод удлинения – замена фактора в числителе исходной факторной системы на сумму однородных показателей. В результате может быть получена смешанная или аддитивная модель с новым набором факторов.
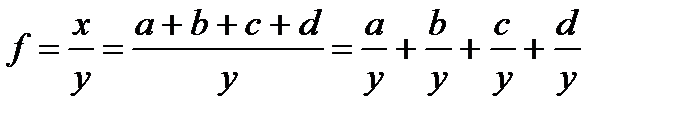
2. Метод формального разложения - замена фактора в знаменателе на сумму однородных показателей. В результате может быть получена смешанная модель
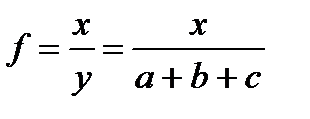
3. Метод расширения – умножение числителя и знаменателя дроби на один или несколько новых показателей. В результате может быть получена мультипликативная или смешанная модель
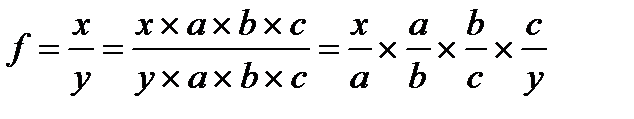
4. Метод сокращения – деление числителя и знаменателя дроби на один и тот же новый показатель. В результате получается кратная, мультипликативная или смешанная модель с новым набором факторов
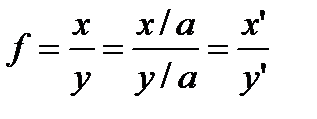
Сложный процесс формирования уровня изучаемого показателя хозяйственной деятельности может быть разложен различными приемами на его составляющие (факторы) и представлен в виде детерминированной факторной системы.
Моделирование мультипликативных факторных системв анализе осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители. Например, при исследовании процесса формирования объема производства продукции можно применять следующие детерминированные модели:
ВП=ЧР*ГВ,
ВП=ЧР*Д*ДВ,
ВП=ЧР*Д*П*ЧВ.
где:
ЧР – среднесписочная численность рабочих
ГВ=Д*ДВ – среднегодовая выработка одного среднесписочного работника
Д – количество отработанных дней одним рабочим за год
ДВ = П*ЧВ = среднедневная выработка одного работника
П – продолжительность рабочего дня, ч
ЧВ – среднечасовая выработка одного рабочего.
Эти модели отражают процесс детализации исходной факторной системы мультипликативного вида и расширения ее за счет расчленения на сомножители комплексных факторов. Степень детализации и расширения модели зависит от цели исследования, а также от возможностей детализации и формализации показателей в пределах установленных правил.
Аналогичным образом, т.е. путем расчленения одного из факторных показателей на составные элементы, осуществляется моделирование аддитивных факторныхсистем.
Как известно, объем реализации продукции равен
VPП = VВП – О н.п.,
где
VВП – объем выпуска продукции;
О н.п. –остатки нереализованной продукции.
Часть нереализованной продукции может находиться на складах предприятия (О скл.),а часть может быть отгружена покупателям, но еще не оплачена (О отгр.). Тогда приведенную исходную модель можно записать следующим образом:
VPП = VВП – Оскл – О отгр.
Стохастические модели. При недостаточном уровне знаний о природе прямых связей того или иного показателя хозяйственной деятельности размах количественных изменений экономических показателей можно выяснить только методами стохастического моделированиямассовых эмпирических данных.
Стохастический анализ направлен на изучение косвенных связей, т.е. опосредованных факторов (в случае невозможности определения непрерывной цепи прямой связи). Из этого вытекает важный вывод о соотношении детерминированного и стохастического анализов: так как прямые связи необходимо изучать в первую очередь, то стохастический анализ носит вспомогательный характер.
Стохастический анализ выступает в качестве инструмента углубления детерминированного анализа факторов, по которым нельзя построить детерминированную модель.
Можно выделить следующие наиболее типичные классы задач анализа хозяйственной деятельности, для решения которых применяются методы стохастического моделирования:
• изучение наличия, направления и интенсивности связей показателей хозяйственной деятельности;
• ранжирование и классификация факторов экономических явлений;
• выявление аналитической формы связи между показателями;
• ранжирование и классификация объектов хозяйствования;
• выявление наиболее информативных (обобщающих) показателей хозяйственной деятельности;
• анализ структурных сдвигов в совокупности объектов анализа;
• нахождение общих закономерностей функционирования объекта;
• построение усредненных нормативов хозяйственной деятельности.
Для решения перечисленных задач применяются такие математико-статистические методы стохастического моделирования, как группировка многомерных наблюдений, корреляционный и регрессионный анализ, дисперсионный анализ, компонентный анализ.
Функционально-стоимостной анализ (ФСА) представляет собой способ системного исследования функций изделий, производственно-хозяйственных процессов или управленческих структур и стоимости этих функций с целью выявления резервов сокращения затрат и нахождения оптимального соотношения между потребительской стоимостью (качеством) объекта и затратами на него.Его основное назначение в том, чтобы выявить ненужные функции этого объекта и предупредить лишние затраты за счет ликвидации ненужных узлов, деталей, упрощения конструкции изделия, замены материалов и т.д.
Как научная дисциплина ФСА (появился в 40-х годах прошлого столетия) получил широкое применение. Главной особенностью ФСА является функциональный подход, при этом функции подразделяются на: основные (выражающие значение объекта), вспомогательные (без которых невозможно осуществить главные целевые функции) и излишние. Соответственно, все затраты подразделяют на функционально-необходимые и излишние затраты, связанные с несовершенством конструкторских решений. Применение того или иного математического метода в экономическом анализе опирается на методологию экономико-математического моделирования хозяйственных процессов и научно обоснованную классификацию методов и задач анализа.
Дата добавления: 2016-04-11; просмотров: 1349;
