Динамическая подвижность белков

Малые колебания атомов в твердом теле происходят с вы­сокими частотами w₀ ~10¹³- c^-l(tau ~ 10¹³с) и малыми амплитудами х_а ~ 0,01-0,1 А - (обычные гармониче­ские колебания). Такой подход неприменим для описания микро­движений белка с амплитудами х_а » 0,1 А. Смещение отдельного фрагмента белка на вели­чину, большую чем 0,1 А, возможно только, если оно одновременно сопро­вождается образованием флуктуационной полости из-за сдвига других моле­кулярных групп, окру­жающих данный фрагмент. Фрагмент бел­ка как бы "расталкивает" соседние группы. Такое движение требует энергии активации для преодоле­ния потенциальных энер­гетических барьеров, препятствующих смеще­нию фрагмента. Посколь­ку переход из одного микросостояния в другое сопровождается больши­ми смещениями (~1А), то и ширина барьера должна быть довольно большой. Такой процесс перехода нельзя уподобить "одноактному" пере­скоку между двумя микроинформационными состояниями. Переход через широкий барьер - непрерывный процесс движения в потенциальном поле со сложным рельефом - частой потен­циальной гребенкой (картинка 1).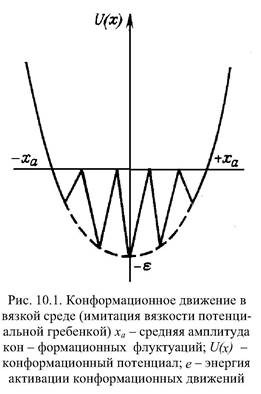

Т.о., движение фрагмента белка характеризуется двумя пространственными масштабами. Движе­ние по "частоколу" из частых потенциальных барьеров отражает взаимо­действие фрагмента с окружающими белковыми группами. Оно носит диффузионный характер и характеризуется коэффициентом конформационной диффузии D(x), зависящим от окружающей среды или от конформационной координаты х. Другой пространственный масштаб отражает результирующее медленное перемещение вдоль самой конформационной координаты и происходит в конформационном потен­циале и (х). Как Выход за пределы конформационной энергетической ямы [-х_а, х_а,] запрещен, так как связанный с остальной белковой молекулой фрагмент не может отойти как угодно далеко. Такое движение соответствует непрерывной ограниченной диффузии в вязкой среде, когда фрагмент испытывает действие случайных толчков или теплового шума. Временная зависимость среднего квадратичного смещения [x(t)]² в этом процессе определяется формулой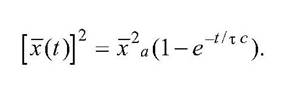

Здесь х² _а - средний квадрат амплитуды смещения, т_с - характерное время релаксации в процессе ограниченной диффузии, зависящее от трения при движении .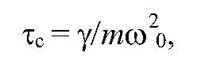

Где y - коэффициент трения, пропорциональный микровязкости белка, т - масса фрагмента, w₀ - частота колебаний. Коэффици­ент трения зависит от микровязкости белка согласно формуле Стокса

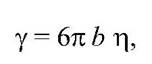
где b - характерный линейный размер фрагмента (b ~ 1 - 10А), ню - вязкость в пуазах (пз). Повышение температуры экспоненциально уменьшает вязкость –

(эпсилон - энергия активации вязкого течения).

С ростом температуры экспоненциально уменьшается и время т_с.

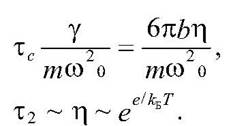
Увеличение вязкости среды приводит к росту т_с т. е. к уменьшению скорости диффузии. Отсюда можно понять влияние температуры на внутримолекулярное движение в белке и зависимость сред­неквадратичного смещения мессбауэровского атома от температуры. .

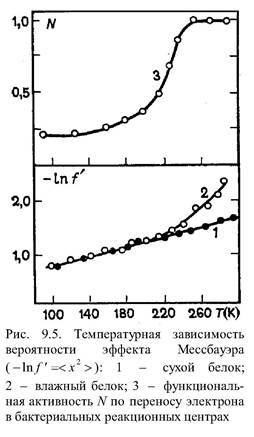
При низких температурах т_с очень велико, и при поглощении у- кванта мессбауэровское ядро не успевает сместиться за время пребыва­ния в возбужденном состоянии. В этом случае происходит поглощение у- кванта без отдачи (f' ~ 1). В области высоких температур, где ню и т_с малы, ядро успевает сместиться и f' падает. Таким образом, при повышении температуры в точке излома температурной кривой изменяется величина т_с, которая становится ниже критического значения. По температурной зависимости f' (Т) можно найти величины микровязкости ню для белков, энергии активации (эпсилон) вязкого течения, ам­плитуды конформационных движений. Имеющие­ся в структуре белка альфа- и бета-элементы испытывают ограниченное диффузионное движение, зависящее от жесткости, микровязкости среды. Изгибные флуктуации альфа-спиралей имеют определенную форму, причем амплитуда и время релаксации резко зависят от линейных размеров спи­рали. В реальных условиях амплитуды изгибных флуктуаций могут дос­тигать нескольких ангстрем, а времена релаксации лежат в микросекундном диапазоне.

Наиболее быстрые и мелкомасштабные флуктуации присущи боковым группам. Эти группы образуют жидкоподобную опушку вокруг спиральных участков полипеп­тидного каркаса и играют роль демпфирующей среды. Иерархия во вре­менах релаксаций позволяет представить динамику белковой глобулы как флуктуации в жидкоподобной капле, армированной упругим поли­пептидным каркасом. Диффузия лигандов внутри глобулы происходит лишь при образовании флуктуационных полостей или "дырок". Появление "дырки" внутри гло­булы может быть инициировано образованием ее вначале в растворителе на поверхности глобулы. Вероятность этого процесса обратно пропорциональна вязкости растворителя. За счет конформационных движений поверхностная группа белка заполняет "дырку" в растворителе. "дырка" теперь оказывается уже в наружном слое белка. Далее, за счет движений групп второго и третьих слоев "дырка" диффундирует внутрь глобулы, обеспечивая появление дополнительных флуктуационных по­лостей. Форма этих полостей в белке непроизвольна, а имеет вид флуктуирующих щелей, параметры которых определяются геометрией жестких элементов белкового каркаса. Решение диффузион­ных уравнений позволяет вычислить скорость диффузии частиц через систему таких флуктуирующих щелей. Так, при диффузии в миоглобине лиганд СО должен пройти несколько "ворот", которые открываются за счет конформационных движений. Скорость диффузии зависит от диа­метра лиганда, амплитуды флуктуации и времени релаксации щели, которая определяется жесткостью и микровязкостью стенок. Общее время прохождения СО в миогло­бине составляет 10^-7 с и соответствует сложению времен конформационных релаксаций нескольких ворот в глобуле. В жесткой молекуле белка, где отсутствуют внутримолекулярные движения и структурные флуктуации, диффузия лиганда должна быть сопряжена с преодолением больших активационных барьеров (до 100 ккал/моль). Эти барьеры настолько замедлят движение лиганда, что оно практически станет бесконечно медленным в масштабах биологического времени. В реальных биополимерах с плотной упаков­кой именно структурные флуктуации делают возможным перенос лигандов внутри молекулы, что важно для ее функциональной активности.