Относительная частота события, статистическое определение вероятности событий.

Примем соглашение: место того, чтобы говорить, произведено n повторений одного и того же опыта, будем говорить, что произведено n опытов.

Событие опыта мы будем обозначать какими либо латинскими буквами или буквами с индексом.

Пусть произведено n опытов, в каждом из которых может появиться или не появиться событие A. И пусть событие наступило m раз, тогда событие 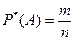(1), называется относительной частотой наступления события A в данной серии из n опытов.

Давно было замечено, что во многих опытах, частота имеет тенденцию стабилизироваться около некоторого числа. Это свидетельствует о том, что данное событие обладает определённой степенью объективной возможности появления опыта, меру которой можно представить в виде относительной частоты.

Это эмпирическое свойство случайных событий носит название устойчивости частот и позволяет ввести понятие статистической вероятности событий.

Статистической вероятностью случайного события называется число, около которого стабилизируется относительная частота появлений этого события при неограниченном увеличении числа повторений опыта.

Вероятность события обозначают записью 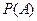. Следовательно, относительного рассмотренного определения, вероятность приближённо равняется частоте. 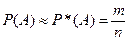(2)

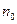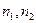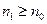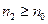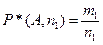
Под стабилизацией частоты около некоторого числа понимается следующее: начиная с некоторого числа , для любых пар натуральных чисел ( , ), , 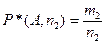относительные частоты появлений события A в 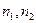сериях опытов мало отличаются друг от друга, и следовательно, любое из них может быть принято за значение вероятности события. В виду такой неоднозначности определения вероятности события согласно формуле в виду практической сложности установлений стабилизации относительной частоты, статистическое определение вероятности события становится неудобным при построении математической модели вероятности этих событий.