Лекция 5. Сетевые модели. Сети Петри.

Сети Петри - это аппарат для моделирования динамических дискретных систем (преимущественно асинхронных параллельных процессов). Сеть Петри определяется как четверка <Р, Т, I, О>, где Р и Т - конечные множества позиций и переходов, I и О -множества входных и выходных функций. Другими словами, сеть Петри представляет собой двудольный ориентированный граф, в котором позициям соответствуют вершины, изображаемые круж­ками, а переходам - вершины, изображаемые утолщенными чер­точками; функциям I соответствуют дуги, направленные от пози­ций к переходам, а функциям О - дуги, направленные от переходов к позициям.

Как и в системах массового обслуживания, в сетях Петри вво­дятся объекты двух типов: динамические, которые изображаются метками (маркерами) внутри позиций, и статические, которым соответствуют вершины сети Петри.

Распределение маркеров по позициям называют маркировкой. Маркеры могут перемещаться в сети. Каждое изменение маркиров­ки называют событием, причем каждое событие связано с опреде­ленным переходом. Считается, что события происходят мгновенно и разновременно при выполнении некоторых условий.

Каждому условию в сети Петри соответствует определенная позиция. Совершению события соответствует срабатывание (воз­буждение или запуск) перехода, при котором маркеры из входных позиций этого перехода перемещаются в выходные позиции. Последовательность событий образует моделируемый процесс.

Правила срабатывания переходов (рис. 1) конкретизируют следующим образом: переход срабатывает, если для каждой из его входных позиций выполняется условие N_i> К_i, где N_i - число маркеров в i-й входной позиции, K_i - число дуг, идущих от i-й пози­ции к переходу; при срабатывании перехода число маркеров в i-й входной позиции уменьшается на К_i, а в j-й выходной позиции уве­личивается на М_j ,где М_j - число дуг, связывающих переход с j-й позицией.

На рис. 1 показан пример распределения маркеров по позициям перед срабатыванием, эту маркировку записывают в виде (2, 2, 3, 1) или (2231). После срабатывания перехода маркировка принимает вид (1,0,1,4).

Можно вводить ряд дополнительных правил и условий в алгоритмы моделирования, получая ту или иную разновидность сетей Петри. Так, прежде всего полезно ввести модельное время, чтобы моделировать не только последовательность событий, но и их привязку ко времени. Это осуществляется приданием переходам веса - продолжительности (задержки) срабатывания, которую можно определять, используя задаваемый при этом алгоритм. Полученную модель называют временной сетью Петри.

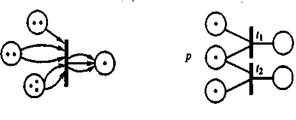
Рис. 1. Фрагмент сети Петри Рис. 2. Конфликтная ситуация

Если задержки являются случайными величинами, то сеть на­зывают стохастической. В стохастических сетях возможно вве­дение вероятностей срабатывания возбужденных переходов. Так, на рис. 2 представлен фрагмент сети Петри, иллюстрирующий конфликтную ситуацию - маркер в позиции p может запустить либо переход t₁ ,либо переход t₂. В стохастической сети предусматрива­ется вероятностный выбор срабатывающего перехода в таких си­туациях.

Если задержки определяются как функции некоторых аргумен­тов, которыми могут быть количество маркеров в каких-либо по­зициях, состояния некоторых переходов и т.п., то сеть называют функциональной.

Во многих задачах динамические объекты могут быть несколь­ких типов, и для каждого типа нужно вводить свои алгоритмы по­ведения в сети. В этом случае каждый маркер должен иметь хотя бы один параметр, обозначающий тип маркера. Такой параметр обычно называют цветом; цвет можно использовать как аргумент в функциональных сетях. Сеть Петри при этом называют цветной.

Среди других разновидностей сетей Петри следует упомянуть ингибиторные сети, характеризующиеся тем, что в них возможны запрещающие (ингибиторные) дуги. Наличие маркера во входной позиции, связанной с переходом ингибиторной дугой, означает запрещение срабатывания перехода.

Введенные понятия поясним на следующих простых примерах.

Пример 1. Требуется описать с помощью сети Петри функционирование системы из предприятий A, В и С. Предприятия А и В поставляют узлы Х1 и X2 соответственно, а на предприя­тии С происходит сборка, в каждый сборочный узел входит один узел X1 и два узла X2. На рис. 1 предприятиям А, В и С соответствуют переходы t₁, t₂ и t₃.

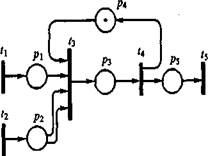
Рис. 3. Сеть Петри для примера 1

Срабатывание перехода t₃ происходит только в том слу­чае, если, во-первых, в позиции p_l имеется метка, а в позиции р₂ - не менее двух меток, что
означает поступление от предприятии А и В соответствующих комплектующих, и, во-вторых, имеется метка в позиции p₄, что означает, что предприятие С закончило сборку предыдущего изделия и готово приступить к сборке следующего. Пока очередное изделие не будет собрано, метки в p₄ не будет, следовательно, запросы, пришедшие во входные позиции р₁ и р₂, вынуждены ожидать срабатывания перехода t₄. Переходам t₁, t₂ и t₃ поставлены в соответствие процедуры вычисления задержек срабатывания. Задержки в первых двух переходах равны интервалам времени между появлениями готовых узлов, задержка в t₃ равна времени сборки изделия.

Пример 2. Требуется описать с помощью сети Петри процес­сы возникновения и устранения неисправностей в некоторой техни­ческой системе, состоящей из М однотипных блоков; в запасе име­ется один исправный блок; известны статистические данные об интенсивностях возникновения отказов и длительностях таких опе­раций, как поиск неисправностей, замена и ремонт отказавшего блока. На рис. 4 представлена соответствующая сеть Петри. Отметим, что при числе меток в позиции, равном М, можно в ней не ставить М точек, а записать в позиции значение М.

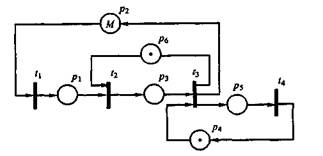
Рис. 4. Сеть Петри для примера 2

В нашем примере значение M в позиции р₂ соответствует числу имеющихся в системе блоков. Переходы отображают следующие события: t₁ - отказ блока, t₂- поиск неисправного блока, t₃ - его за­мена, t₄ - окончание ремонта.

Очевидно, что при непустой позиции р_г переход t₁ срабатывает, но с задержкой, равной вычисленному случайному значению мо­делируемого отрезка времени между отказами. После выхода маркера из t₁ он попадает через р₁ в t₂, если имеется метка в пози­ции р₆, это означает, что обслуживающая систему бригада специа­листов свободна и может приступить к поиску возникшей неисп­равности. В переходе t₂ метка задерживается на время, равное случайному значению длительности поиска неисправности. Далее маркер оказывается в р₃ и если имеется запасной блок (маркер в р₄), то запускается переход t₃, из которого маркеры выйдут в р₂ , р₅ и р₆ через отрезок времени, требуемый для замены блока. После этого в t₄ имитируется восстановление неисправного блока.

Рассматриваемая модель описывает функционирование систе­мы в условиях, когда отказы могут возникать и в рабочем, и в неисправном состояниях системы. Поэтому не исключены ситуа­ции, при которых более чем один маркер окажется в позиции р₁.