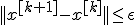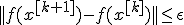Теорема 1 о сходимости метода градиентного спуска спуска с постоянным шагом.
Метод градиентного спуска
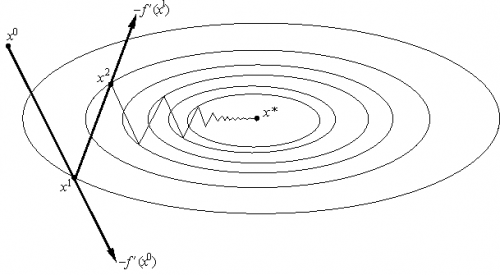
Рис.1 Геометрическая интерпретация метода градиентного спуска с постоянным шагом. На каждом шаге мы сдвигаемся по вектору антиградиента, "уменьшенному в 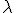 раз".
раз".
Идея метода
Основная идея метода заключается в том, чтобы осуществлять оптимизацию в направлении наискорейшего спуска, а это направление задаётся антиградиентом 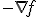 :
:
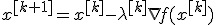
где 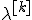 выбирается
выбирается
- постоянной, в этом случае метод может расходиться;
- дробным шагом, т.е. длина шага в процессе спуска делится на некое число;
- наискорейшим спуском:
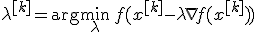
Алгоритм
Вход: функция 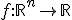
Выход: найденная точка оптимума 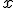
- Повторять:
-
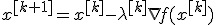 , где
, где 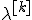 выбирается одним из описанных выше способов
выбирается одним из описанных выше способов - если выполен критерий останова, то возвращаем текущее значение
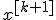
Критерий останова
Критерии остановки процесса приближенного нахождения минимума могут быть основаны на различных соображениях. Некоторые из них:
Здеcь 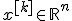 - значение, полученное после
- значение, полученное после 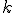 -го шага оптимизации.
-го шага оптимизации.  - наперед заданное положительное число.
- наперед заданное положительное число.
Сходимость градиентного спуска с постоянным шагом
Теорема 1 о сходимости метода градиентного спуска спуска с постоянным шагом.
Пусть 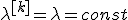 , функция
, функция 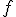 дифференцируема, ограничена снизу. Пусть выполняется условие Липшица для градиента
дифференцируема, ограничена снизу. Пусть выполняется условие Липшица для градиента 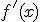 :
: 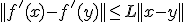 . Пусть
. Пусть 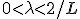 .
.
Тогда 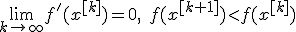 при любом выборе начального приближения.
при любом выборе начального приближения.
В условиях теоремы градиентный метод обеспечивает сходимость 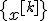 либо к точной нижней грани
либо к точной нижней грани 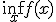 (если функция
(если функция 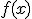 не имеет минимума) либо к значению
не имеет минимума) либо к значению 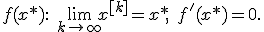 Существуют примеры, когда в точке
Существуют примеры, когда в точке 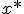 реализуется седло, а не минимум. Тем не менее, на практике методы градиентного спуска обычно обходят седловые точки и находят локальные минимумы целевой функции.
реализуется седло, а не минимум. Тем не менее, на практике методы градиентного спуска обычно обходят седловые точки и находят локальные минимумы целевой функции.
Определение. Дифференцируемая функция 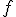 называется сильно выпуклой (с константой
называется сильно выпуклой (с константой 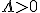 ), если для любых
), если для любых 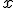 и
и 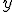 из
из 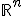 справедливо
справедливо
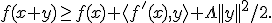
Дата добавления: 2016-03-30; просмотров: 1386;