Силы инерции кривошипно-шатунного механизма и силы давления газов
После приведения масс движущихся частей кривошипно-щатунного механизма к двум массам mr и mj силы инерции этих масс находят из условий их движения.
Силы инерции возвратно-поступательно движущихся масс вычисляют по формуле:
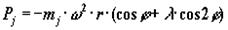 ,
,
где  –сила инерции первого порядка; период изменения этой силы – один оборот коленчатого вала;
–сила инерции первого порядка; период изменения этой силы – один оборот коленчатого вала;
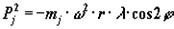 –сила инерции второго порядка; период изменения этой силы – пол-оборота коленчатого вала.
–сила инерции второго порядка; период изменения этой силы – пол-оборота коленчатого вала.
Эти силы действуют по оси цилиндра и считаются положительными, если они направлены к оси коленчатого вала, и отрицательными, если направлены от коленчатого вала (рис. 1.26).
Сила инерции вращающихся масс действует по радиусу кривошипа и определяется по формуле:
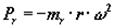 .
.
Силы давления газов в цилиндре двигателя в зависимости от хода поршня определяют по индикаторной диаграмме, построенной по данным теплового расчета или полученной экспериментально.
Сила давления газов на поршень, действующая по оси цилиндра, равна:
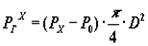 ,
,
где PX – давление газов в цилиндре двигателя, определяемое для соответствующего положения поршня (X) по индикаторной диаграмме;
P0– давление в картере, принимаемое обычно равным давлению окружающей среды;
D – площадь поршня.
Для динамического расчета двигателя, а также для расчета на прочность его деталей необходимо иметь зависимость PГ = f(?) (рис. 1.26).
Сила PГ считается положительной, если она направлена к оси коленчатого вала.
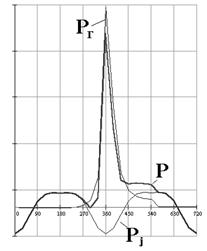
Рис. 1.26. Графики сил PГ, Рj и Р по углу поворота коленчатого вала
Складывая алгебраически силы, действующие в направлении оси цилиндра, получим суммарную силу, действующую на КШМ, для каждой точки Х положения поршня
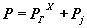 .
.
Диаграмма изменения этой силы по углу поворота коленчатого вала (для оборотов, соответствующих максимально эффективной мощности) представлена на рис. 1.26.
Дата добавления: 2016-02-16; просмотров: 713;
