Логические действия с суждениями.
1. Виды сложных суждений. Сложное суждение – это суждение, в структуру которого входит два и более субъектов, или два и более предикатов, или два и более субъектов и предикатов, или иначе – два и более простых суждения.
Это значит, что сложное суждение образуется из простых (т.е. сложное суждение содержит два или более суждений) с помощью логических связок, которым отвечают логические операции, которые отражаются символами логических операций, или логическими операторами.
| Логическая связка | Логическая операция | Символ логической операции |
| «и» | конъюнкция (от лат. conjunctio – связь, объединение) |
 , & , &
|
| «или» | дизъюнкция (слабая, нестрогая) (от лат disjunctio – разъединение, различение) |
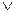
|
| «или, или» | сильная (строгая) дизъюнкция | 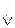
|
| «если, то» | импликация (от лат. implico – тесно связываю) | → |
| «если и только если, то» | эквиваленция (тождество) (от лат. aequivalens – равноценный) | ↔ , ≡ |
| неправильно, что А или просто: «не-А» | отрицание | ~А , Ā |
Основные виды сложных суждений (в соответствии с функциями логических связок) разделяют на безусловные и условные:
Безусловное суждение – это суждение, в котором отсутствует зависимость утверждения или отрицания от любых других обстоятельств. Такое суждение определяется с помощью связок «и», «или», «или, или».
Формула: S есть Р 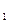 и Р
и Р 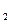 , S есть Р
, S есть Р 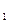 или Р
или Р 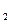 , S есть или Р
, S есть или Р 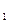 , или Р
, или Р 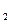 .
.
Среди безусловных суждений выделяют: соединительные и разделительные, разделяющие и множественные:
– соединительное (конъюнктивное) – это суждение, содержащее определенное утверждение или отрицание о принадлежности предмету двух или более признаков, которое образовано в результате операции конъюнкции, т.е. соединенных между собой логической связкой «и».
Формула: «Все (некоторые, данный) S есть Р 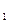 и Р
и Р 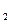 » («М. В. Ломоносов был ученым и поэтом»). В естественном языке эти суждения могут быть выражены не только, когда (1) связующая связка выражена в сложном предикате (S есть Р
» («М. В. Ломоносов был ученым и поэтом»). В естественном языке эти суждения могут быть выражены не только, когда (1) связующая связка выражена в сложном предикате (S есть Р 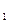 и Р
и Р 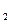 ), но и когда (2) связующая связка выражена в сложном субъекте (S
), но и когда (2) связующая связка выражена в сложном субъекте (S 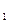 и S
и S 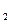 есть Р), а также когда (3) связующая связка выражена в сложном субъекте и сложном предикате (S
есть Р), а также когда (3) связующая связка выражена в сложном субъекте и сложном предикате (S 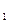 и S
и S 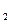 есть Р
есть Р 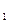 и Р
и Р 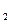 ). Конъюнктивной связке присуще качество коммутативности. Это значит, что А
). Конъюнктивной связке присуще качество коммутативности. Это значит, что А В≡В
В≡В А. Также конъюнктивной связке свойственно качество ассоциативности. Это значит, что изменение сочетания конъюнктов в суждении (А
А. Также конъюнктивной связке свойственно качество ассоциативности. Это значит, что изменение сочетания конъюнктов в суждении (А В)
В)  С на А
С на А (В
(В С) не изменяет смысла исходного связующего суждения. Это выражение можно записать без скобок: А
С) не изменяет смысла исходного связующего суждения. Это выражение можно записать без скобок: А В
В С;
С;
– разделительное (дизъюнктивное) – это суждение, в предикате которого отмечается о принадлежности/непринадлежности предмету двух или более признаков, но не утверждается, что все признаки обязательно принадлежат предмету суждения, которое образовано в результате операции дизъюнкции из простых суждений, соединенных между собой логической связкой «или», «или, или».
Формула: S есть Р 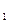 или Р
или Р 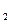 , S есть или Р
, S есть или Р 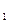 , или Р
, или Р 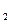 .
.
Среди разделительных суждений выделяют исключающе-разделительные и соединительно-разделительные суждения.
– исключающе-разделительное(сильная дизъюнкция) – это суждение, в котором речь идет о принадлежности (или непринадлежности) предмету только одного (но неизвестно, какого именно) из перечисленных признаков.
Формула: S есть или Р 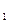 , или Р
, или Р 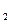 («Он или флегматик, или холерик»);
(«Он или флегматик, или холерик»);
– соединительно-разделительное(слабая дизъюнкция) – это суждение, в котором речь идет о принадлежности (или непринадлежности) предмету хотя бы одного из перечисленных признаков.
Формула: S есть Р 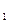 или Р
или Р 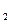 («Он работает или учится»).
(«Он работает или учится»).
Разделительная связка может выражаться не только (1) в сложном предикате (S есть Р 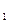 или Р
или Р 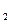 ), но и (2) в сложном субъекте (S
), но и (2) в сложном субъекте (S 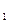 или S
или S 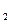 есть Р), а также (3) в сложном субъекте и сложном предикате (S
есть Р), а также (3) в сложном субъекте и сложном предикате (S 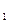 или S
или S 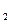 есть Р
есть Р 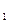 или Р
или Р 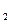 ). Как и конъюнкции, дизъюнкции присуще качество коммутативности: А
). Как и конъюнкции, дизъюнкции присуще качество коммутативности: А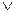 В≡В
В≡В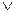 А. Дизъюнкции свойственно и качество ассоциативности, потому изменения в сочетании членов разделительного суждения (напр., (А
А. Дизъюнкции свойственно и качество ассоциативности, потому изменения в сочетании членов разделительного суждения (напр., (А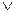 В)
В)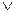 С на А
С на А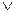 (В
(В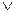 С)) не изменяют содержания суждения. Его также можно записать без скобок А
С)) не изменяют содержания суждения. Его также можно записать без скобок А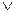 В
В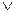 С. В логике различают полную и неполную дизъюнкции;
С. В логике различают полную и неполную дизъюнкции;
– разделяющее – это суждение, в котором отмечается полный перечень видов (вариантов) предмета мысли («Теперь в Южном полушарии лето, зима, осень или весна»);
– множественное – это суждение, в котором отражается общность признаков различных предметов и классов предметов («Все пассажирские пароходы и некоторые самолеты могут плавать и перевозить людей»).
Условное (импликативное)– это суждение, в котором отражается зависимость того или другого явления от любых обстоятельств, образовавшееся в результате операции импликации из простых суждений, соединенных между собой логической связкой «если, то».
Формула: Если S есть Р, то S 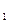 есть Р
есть Р 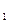 .
.
Импликация состоит из логического основания – «если» и логического следствия – «то» («Если закончится учебный год, то начнутся каникулы»).
По характеру отношения между содержанием следствия и содержанием основанияопределяют выделяющие и невыделяющие суждения:
– выделяющее – это суждение, в котором то, о чем идет речь в основании, является достаточным и необходимым для существования того, о чем идет речь в следствии, и наоборот, то, о чем идет речь в следствии является достаточным и необходимым для существования того, о чем идет речь в основании.
Формула: «S тогда и только тогда, когда Р» («Студент получит диплом ДонНТУ, если пройдет полный курс обучения в этом университете»);
– невыделяющее – это суждение, в котором утверждается, что существование того, о чем идет речь в основании, является условием достаточным, но не необходимым для существования того, о чем идет речь в следствии, а то, о чем идет речь в следствии, является необходимым, но недостаточным условием существования того, о чем идет речь в основании (т.е. основание здесь является достаточным, но не необходимым для наступления соответствующего следствия) («Если человек посетит библиотеку, то он сможет получить информацию по вопросам, относительно которых там есть книги»).
Эквивалентное – это условное суждение, в котором образующие его простые суждения связаны между собой эквивалентной связкой («если и только если, то»).
Формула: Если А, то В, и если В, то А («Иванов не завершит свою курсовую работу к сроку, если и только если ему не помогут однокурсники»).
Сложные суждения, как и простые, могут быть утвердительными и отрицательными.
Сложные суждения являются утвердительными в том и только в том случае, если все составляющие его простые суждения являются положительными («Наступила ночь и небо зажглось мириадами звезд»).
Сложные суждения являются отрицательными в том и только в том случае, если все составляющие его простые суждения являются отрицательными («Общественное сознание не есть сумма индивидуальных сознаний и не тождественно духовной жизни общества»).
Сложные суждения являются неопределенными, если часть составляющих его простых суждений являются утвердительными, а часть – отрицательными («В рыночной экономике товары не продаются по их стоимости, но продаются по цене производителя»).
Логическая форма сложного суждения – это его запись символическим языком логики, в котором простые суждения заменены переменными а,b.
В логике большое значение имеет истинность сложных суждений. Истинность сложных суждений зависит от истинных значений простых суждений, входящих в состав сложного, и от типа связок.
В сложном суждении простые суждения (или их заменяющие переменные) соединяются логическими связками: конъюнкции, дизъюнкции, импликации, эквиваленции и отрицания:
– конъюнктивное, илисоединительноесуждение – это сложное суждение, в котором простые суждения связаны союзом «и». Конъюнктивная связка (одно рядом и одновременно с другим) обозначается символом«  ».Формула конъюнктивного суждения:а
».Формула конъюнктивного суждения:а  b: «Т. Г. Шевченко был художником и поэтом».
b: «Т. Г. Шевченко был художником и поэтом».
Простые суждения, выступающие в качестве элементов соединительного суждения, называются конъюнктами. Минимальное число конъюнктов – два, максимальное – неограниченно. В сложном соединительном суждении не все перечисленные конъюнкты могут быть заменены оборотом «и другие» и аналогичными словосочетаниями. Если в конъюнктивном суждении перечислены не все конъюнкты, то оно неполное, или открытое. Если в конъюнктивном суждении перечислены все конъюнкты, то оно полное, или закрытое.
Истинность сложных суждений обусловлена истинностью составляющих их простых суждений. Для определения их истинности в логике используются таблицы истинности. В них фиксируются истинностные характеристики составляющих сложное суждение простых суждений и сложного суждения в целом. В таблице обозначаются: истинность – «1», неистинность – «0».
Таблица истинности конъюнкции
| a | b | a  b b
|
Таблица отражает структурный закон конъюнкции: сложное соединительное суждение истинно тогда и только тогда, когда все конъюнкты истинны.
Если хотя бы одно из составляющих конъюнкцию простых суждений неистинно, то конъюнктивное суждение в целом неистинно независимо от количества конъюнктов.
В естественном языке конъюнкция (союз «и» – символ «  ») выражается разделительными союзами «а», «но», «да», предлогами «как, так и», «не только, но и», вводными словами и словосочетаниями «однако», «хотя», «несмотря на», союзными словами «также», «тоже» и др.: «Богословское образование в ряде стран дают также теологические факультеты при некоторых светских учебных заведениях». Логический союз конъюнкции может быть выражен однородными членами предложения, связанными по смыслу без союзов: «Одна часть создаваемой рабочей силой новой стоимости возмещает авансированный переменный капитал, вторая часть образует прибавочную стоимость», где два простых двухместных (бинарных) конъюнкта связаны не употребленным логическим союзом «и»;
») выражается разделительными союзами «а», «но», «да», предлогами «как, так и», «не только, но и», вводными словами и словосочетаниями «однако», «хотя», «несмотря на», союзными словами «также», «тоже» и др.: «Богословское образование в ряде стран дают также теологические факультеты при некоторых светских учебных заведениях». Логический союз конъюнкции может быть выражен однородными членами предложения, связанными по смыслу без союзов: «Одна часть создаваемой рабочей силой новой стоимости возмещает авансированный переменный капитал, вторая часть образует прибавочную стоимость», где два простых двухместных (бинарных) конъюнкта связаны не употребленным логическим союзом «и»;
– дизъюнктивное, или разъединительное сложное суждение делят на дизъюнкцию нестрогую (слабую) и дизъюнкцию строгую (сильную):
– дизъюнкция нестрогая, или слабая – это сложное суждение, в котором простые суждения связаны союзом «или». Дизъюнктивная связка (одно из двух) обозначается символом « 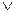 ». Формула нестрогого дизъюнктивного суждения – а
». Формула нестрогого дизъюнктивного суждения – а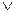 b:«Л. Н. Толстой был писателем или поэтом».
b:«Л. Н. Толстой был писателем или поэтом».
Простые суждения, выступающие в качестве элементов соединительного суждения, называются дизъюнктами. Минимальное число дизъюнктов – два, максимальное – неограниченно. В сложном соединительном суждении не все перечисленные дизъюнкты могут быть заменены оборотом «и другие» и аналогичными словосочетаниями. Если в дизъюнктивном суждении перечислены не все дизъюнкты, то оно неполное, или открытое. Если в дизъюнктивном суждении перечислены все дизъюнкты, то оно полное, или закрытое.
Таблица истинности нестрогой дизъюнкции
| a | b | a 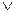 b b
|
Таблица отражает структурный закон дизъюнкции: нестрогое разъединительное суждение истинно тогда и только тогда, когда истинным является хотя бы один дизъюнкт истины.
Если все составляющие нестрогую дизъюнкцию простые суждения неистинны, то дизъюнктивное суждение неистинно в целом независимо от количества дизъюнктов.
В естественном языке нестрогая дизъюнкция (союз «или» – символ « 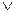 ») выражается только разделительными союзами «или», «либо». Логический союз дизъюнкции нетождественен применяемым в предложениях разделительным союзам «а», «но», «да», разделительным частицам «то, то», «не то, не то» и др.;
») выражается только разделительными союзами «или», «либо». Логический союз дизъюнкции нетождественен применяемым в предложениях разделительным союзам «а», «но», «да», разделительным частицам «то, то», «не то, не то» и др.;
– дизъюнкция строгая, илисильная – это сложное суждение, в котором простые суждения связаны союзом «или, или». Дизъюнктивная связка (или одно, или другое) обозначается символом « 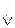 ». Формула строгого дизъюнктивного суждения – а
». Формула строгого дизъюнктивного суждения – а 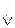 b: «Он добрался до Австралии или самолетом, или теплоходом». Дизъюнкты строгой, или сильной дизъюнкции называются альтернативами. «Он добрался до Австралии самолетом» и «Он добрался до Австралии теплоходом» – две альтернативы суждения, которые одновременно истинными быть не могут. В сильной дизъюнкции может применяться и союз «или», но только в разделительном смысле, а не в разделительно-соединительном как это в нестрогой дизъюнкции. Строгая и нестрогая дизъюнкции различаются по характеру связи дизъюнктов.
b: «Он добрался до Австралии или самолетом, или теплоходом». Дизъюнкты строгой, или сильной дизъюнкции называются альтернативами. «Он добрался до Австралии самолетом» и «Он добрался до Австралии теплоходом» – две альтернативы суждения, которые одновременно истинными быть не могут. В сильной дизъюнкции может применяться и союз «или», но только в разделительном смысле, а не в разделительно-соединительном как это в нестрогой дизъюнкции. Строгая и нестрогая дизъюнкции различаются по характеру связи дизъюнктов.
Таблица истинности строгой дизъюнкции
| a | b | a 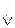 b b
|
Таблица отражает структурный закон строгой дизъюнкции: строгое разделительное суждение истинно тогда и только тогда, когда только один из дизъюнктов необходимо истинен.
Если из составляющих строгую дизъюнкцию простых суждений истинны все, или некоторые, или все неистинны, то строгое дизъюнктивное суждение в целом неистинно независимо от количества дизъюнктов.
В естественном языке сильная дизъюнкция (повторяющиеся союзы «или, или» – символ « 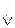 ») выражается теми же союзами, что и в слабой дизъюнкции;
») выражается теми же союзами, что и в слабой дизъюнкции;
– импликативное, или условноесуждение – это сложное суждение, в котором простые суждения связаны союзом«если, то». Импликативная связка(если есть первое, то обязательно есть и второе) обозначается символом «→». Формула импликативного суждения – а→b:«Если студент-бюджетник учится на «отлично», то он получает повышенную стипендию».
Импликативные суждения отражают пространственно-временные, функциональные, причинно-следственные и другие зависимости предметов.
Простое суждение, в котором отражается условие выраженной в импликативном суждении зависимости предметов или признаков, называется антецедентом (от лат. antecendens – предшествующий), или основанием.
Простое суждение, в котором отражается обусловленное явление выраженной в импликативном суждении зависимости, называется консеквентом (от лат. cjnsequens – последующий), или следствием.
Грамматически антецедент может быть расположен до и после консеквента.
Таблица истинности импликации
| a | b | a→b |
Таблица отражает структурный закон импликации: условное суждение неистинно тогда и только тогда, когда антецедент (первая часть импликации) истинен, а консеквент (вторая часть импликации) неистинен; во всех других случаях импликация истинна.
В естественном языке импликация (союз «если, то» – символ «→») выражается: «потому, что», «так как», «следовательно», «исходя из того, что», «постольку, поскольку» и др. Грамматическое выражение импликативного союза может отсутствовать, заменяться знаком «тире»;
– суждение эквиваленции, или тождества – это сложное суждение, в котором простые суждения связаны союзом «если и только если, то». Эквивалентная связка(первое есть только в том случае, если есть второе) обозначается символом «≡», либо символом «↔». Формула суждения эквиваленции – а≡b, либо а↔b:«Только при условии, если закончится учебный год, то начнутся каникулы».
Таблица истинности эквиваленции
| a | b | a↔b |
Таблица отражает структурный закон эквиваленции: суждение тождества истинно, только если все составляющие его простые суждения истинны, либо неистинны одновременно.
Если простые суждения, составляющие эквиваленцию, противоположны по истинностной характеристике, то суждение тождества в целом неистинно.
В естественном языке эквиваленция (союз «если и только если, то» – символ «≡»,либо«↔») выражается: «тогда и только тогда, когда», «тот и только тот», «в том и только в том случае, если», «только исходя из того, что», «только при одном условии, согласно которому» и др.;
– отрицание превращает истинное суждение в неистинное, а неистинное – в истинное. Отрицание соединяет простые суждения с помощью одно местной унарной связки «не» (читается как «неправильно, что»: «Меркурий не является большой планетой» являет собой отрицание суждения «Меркурий является большой планетой»).
При отрицании простых категорических суждений их качество и количество изменяется на противоположное:
~A=О ~О=А ~Е=І ~І=Е
Отрицание сложных суждений происходит в соответствии со следующей эквивалентностью:
~ (A  B)равносильно ~A
B)равносильно ~A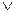 ~B;
~B;
~ (A 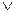 B)равносильно ~A
B)равносильно ~A  ~В;َ
~В;َ
~ (A→B)равносильно A  ~В;َ
~В;َ
~ (A=B)равносильно(~A  B)
B) 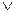 (A
(A  ~B);
~B);
~ (A 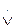 B)равносильно A=B.
B)равносильно A=B.
Таблица истинности отрицания
| a | ~a |
Сложные суждения могут быть комбинированными. Комбинированное – это сложное суждение, в котором составляющие его простые суждения связаны логическими союзами разных видов. Виды логических союзов могут применяться в сложных суждениях в произвольных сочетаниях. При этом существенным является порядок связи простых суждений в сложном суждении, позволяющий выявить основной логический союз комбинированного суждения.
Так, в суждении (a b)→c основным (сложный антецедент) является логический союз импликации и комбинированное соединительно-условное суждение будет импликативным суждением. Если изменить последовательность связи простых суждений a
b)→c основным (сложный антецедент) является логический союз импликации и комбинированное соединительно-условное суждение будет импликативным суждением. Если изменить последовательность связи простых суждений a (b→c), то основным (антецедентом) станет логический союз конъюнкции и... суждение будет конъюнктивным.
(b→c), то основным (антецедентом) станет логический союз конъюнкции и... суждение будет конъюнктивным.
2. Отношения между видами сложных суждений. Отношения между сложными суждениямибывают сравнимые и несравнимые.
Сравнимые сложные суждения – это суждения, которые состоят из одних и тех же (тождественных) простых суждений, но различаются логическими союзами: «Студент хорошо учится и получает знание» (a b) и «Если студент хорошо учится, то он получает знание» (a→b).
b) и «Если студент хорошо учится, то он получает знание» (a→b).
Несравнимые сложные суждения – это суждения, в которых хотя бы одно простое суждение не совпадает: «Он является студентом и спортсменом» (aÙb) и «Он является студентом и поэтом» (a с).
с).
Сравнимые суждения могут быть совместимыми и несовместимыми:
– совместимые – это суждения, которые при одинаковых наборах значений простых суждений могут быть одновременно истинными;
– несовместимые– это суждения, которые при одинаковых наборах значений простых суждений не могут быть одновременно истинными.
Виды отношений между совместимыми суждениями:
– эквивалентности – это суждения, где при одинаковых наборах значений их переменных они приобретают одни и те же значения: «А. С. Пушкин – поэт и писатель» и «А. С. Пушкин – писатель и поэт».
Сложные суждения тождественны лишь в том случае, если они имеют одинаковые истинностные характеристики при одинаковых истинностных характеристиках составляющих их простых суждениях.
Дата добавления: 2016-02-16; просмотров: 2798;
