Надежность систем с облегченным резервом
НАДЕЖНОСТЬ СИСТЕМ С ОБЛЕГЧЕННЫМ И СО СКОЛЬЗЯЩИМ РЕЗЕРВОМ
Надежность систем с облегченным резервом
Как отмечалось в предыдущих лекциях, ненагруженный резерв более эффективен, чем нагруженный, и количественно показатели эффективности зависят от законов распределения наработки до отказа отдельных элементов резервированной системы.
Основным моментом, который может сказаться на оценке надежности является то, что предположение 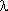 = const является довольно условным, поскольку, особенно при отсутствии технического обслуживания, очередной работающий элемент эксплуатируется до полного износа (физически
= const является довольно условным, поскольку, особенно при отсутствии технического обслуживания, очередной работающий элемент эксплуатируется до полного износа (физически 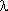 должна возрастать). Поэтому принятое экспоненциальное распределение наработки элементов, переходящих из резервных в рабочие, использовалось только с целью упрощения расчетов.
должна возрастать). Поэтому принятое экспоненциальное распределение наработки элементов, переходящих из резервных в рабочие, использовалось только с целью упрощения расчетов.
Ненагруженный резерв в рамках принятых допущений не всегда осуществим. Например, в авиа- и судовых системах как основные, так и резервные элементы подвержены вибрации, ударам, повторно-статическим нагрузкам, перепадам температур и т. п. Поэтому не включенные в работу резервные элементы будут иметь некоторую 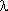
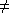 0, то есть они также изнашиваются, но менее интенсивно.
0, то есть они также изнашиваются, но менее интенсивно.
Поэтому, в ряде практических случаев, уместно применять облегченный резерв:
( подключение резервных элементов (РЭ) к цепям питания для прогрева и удержания требуемых значений параметров;
( внешние нагрузки и воздействия, приводящие к изменению свойств материалов, рабочих параметров и т. п.
При этом, РЭ будут иметь некоторую интенсивность отказов 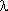 р
р 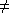 0 .
0 .
Рассмотрим систему, состоящую из равнонадежных основного (ОЭ) и резервного (РЭ) элементов. Элементы невосстанавливаемые.
События, обеспечивающие безотказную работу (БР) системы за наработку (0, t ):
A = {БР системы за наработку (0, t )};
A1 = {БР ОЭ за наработку (0, t )};
A2 = {отказ ОЭ в момент  < t, включение РЭ и БР его на интервале (t -
< t, включение РЭ и БР его на интервале (t -  )}.
)}.
Событие A представляет сумму событий A1 и A2
A = A1 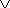 A2
A2

ВБР системы за наработку (0, t ), т.е. к наработке t равна сумме вероятностей событий A1 и A2:
P(A) = P( A1 ) + P( A2 ) ,
где P(A) = Pс( t ) – ВБР системы к наработке t;
P(A) = P0 ( t ) – ВБР ОЭ к наработке t (за интервал (0, t ));
P(A) = Pр ( t ) – ВБР РЭ к наработке t, при условии, что ОЭ отказал.
При известном законе распределения наработки ОЭ вычисление P0 ( t ) не составляет труда, подробнее рассмотрено определение Pр ( t ).
Для этого событие A2 раскладывается на составляющие:
A21 = {отказ ОЭ при наработке  < t};
< t};
A22 = {БР РЭ до наработки  – момент включения его в работу};
– момент включения его в работу};
A23 = {БР РЭ от  до t, т.е. за интервал (t -
до t, т.е. за интервал (t -  )}.
)}.
Очевидно, событие A2 выполнится при одновременном выполнении всех событий:
A2 = A21 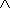 A22
A22  A23 ;
A23 ;
События A21, A22, A23 являются зависимыми, но поскольку они представляют ВБР или ВО элементов, наработки до отказа которых описываются своими законами распределения, то вероятность события A2 равна произведению вероятностей событий:
P( A2 ) = P( A21 ) · P( A22 ) · P( A23 ) .
Соответствующие вероятности определяются:
Выделяется бесконечно малый интервал [  ,
,  + d
+ d  ] и определяется вероятность отказа ОЭ в интервале [
] и определяется вероятность отказа ОЭ в интервале [  ,
,  + d
+ d  ]:
]:
f0 (  ) = - dP0 (
) = - dP0 (  ) / d
) / d  – ПРО ОЭ.
– ПРО ОЭ.
ВБР РЭ до момента  отказа ОЭ
отказа ОЭ
Pр (  ) = P( A22 )
) = P( A22 )
ВБР РЭ от момента  включения в работу до t
включения в работу до t
Pр (t -  ) = P( A23 ) .
) = P( A23 ) .
Тогда ВБР ОЭ в течение наработки [  ,
,  + d
+ d  ] при условии, что ОЭ отказал, равна:
] при условии, что ОЭ отказал, равна:
Pр (  ) · Pр (t -
) · Pр (t -  ) · f0 (
) · f0 (  ) d
) d  .
.
Полученное выражение не равно P( A2 ), поскольку выражает ВБР за выделенный бесконечно малый интервал наработки вблизи  .
.
Поскольку  < t, то из полученного выражения искомая вероятность Pр ( t ) = P( A2 ), получена интегрированием выражения по всем
< t, то из полученного выражения искомая вероятность Pр ( t ) = P( A2 ), получена интегрированием выражения по всем  от 0 до t.
от 0 до t.
Окончательно:
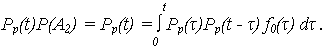
Тогда ВБР резервируемой системы с облегченным резервом:

Аналогично, ВБР системы, состоящей из n равнонадежных элементов:
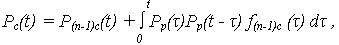
где индекс (n-1)с означает, что ВБР и ПРО относятся к системе, при отказе которой включается рассматриваемый n –й элемент.
При экспоненциальном распределении наработки до отказа элементов составляющие расчетного выражения принимают вид:
Pр (  ) = exp(- ) = exp(- 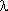 p p  ); );
| ||
Pр (t -  ) = exp { - ) = exp { - 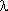 раб (t - раб (t -  )}; )};
| ||
f0 (  ) = ) = 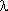 раб exp ( - раб exp ( - 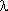 раб · раб ·  ); );
| ||
P0 ( t ) = exp ( - 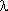 раб · t ), раб · t ),
|
где 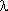 раб – ИО элементов в рабочем режиме;
раб – ИО элементов в рабочем режиме; 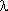 p – ИО элементов в режиме резерва.
p – ИО элементов в режиме резерва.
При наличии одного ОЭ и одного РЭ (n = 2), ВБР определяется:
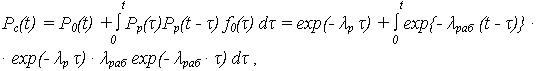
окончательно:
Pс ( t ) = exp ( - 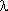 раб · t )[1 +
раб · t )[1 + 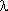 раб {1 - exp ( -
раб {1 - exp ( - 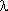 pt )} /
pt )} / 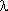 p] .
p] .
Для системы из n элементов с экспоненциальной наработкой до отказа
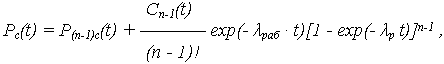
где 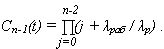
Расчеты для систем с облегченным резервом имеют объективные трудности, поскольку очень трудно учесть как влияет нагрузка, внешние воздействия на характеристики надежности.
Средняя наработка до отказа системы из n элементов:
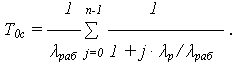
Для практических расчетов систем с облегченным резервированием в случае, если ОЭ имеет распределением наработки P0 ( t ) = exp ( - 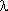 раб · t ) и идентичные резервные элементы (РЭ)
раб · t ) и идентичные резервные элементы (РЭ)
Pр ( t ) = exp (- 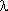 pt ) – для( n - 1 ) резервных элементов,
pt ) – для( n - 1 ) резервных элементов,
ВБР системы может быть приближенно определена по выражению:
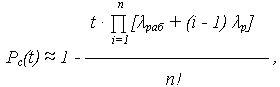
где n – общее число элементов системы.
Например, при n = 2 (k = 1, m = 1)
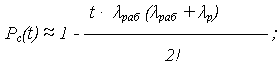
при n = 3 (k = 2, m = 1)
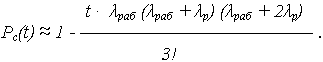
Дата добавления: 2016-03-20; просмотров: 1129;
