Основы теории использования энергии ветра
Воздушный поток, как и всякое движущееся тело, обладает кинетической энергией. Одним из видов использования кинетической энергии является превращение ее в механическую работу.
Кинетическая энергия Ев воздушного потока, имеющего скорость v, определяется по выражению
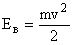
| (2.8) |
где m – масса движущегося воздушного потока;
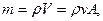
| (2.9) |
где V – объем массы воздуха, протекающего за секунду через сечение А со скоростью v.
Количество энергии ветра, протекающего за 1 с через поперечное сечение:
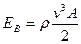
| (2.10) |
Энергия ветра изменяется пропорционально площади поперечного сечения ветрового потока и кубу его скорости.
Отличительным свойством ветра является его повсеместность. Однако техническое использование энергии ветра во многих случаях крайне затруднено из-за низкой плотности воздуха (она в 800 раз меньше плотности воды). Для получения значительной мощности необходимо ветроколесо очень больших размеров, т.к. ветроагрегат может преобразовать только часть потенциальной энергии, определяемой коэффициентом использования энергии ветра x. При этом частота вращения ветроколеса должна регулироваться из-за непостоянства скорости ветра во времени и вырабатываемая мощность, изменяясь пропорционально третьей степени скорости ветра, будет иметь большую амплитуду колебаний.
Мощность, развиваемая ветроколесом
Мощность эта определяется как кинетическая энергия ветра, действующая в единицу времени, с учетом коэффициента ее использования:
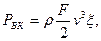 Вт Вт
| (2.11) |
где x- коэффициент использования энергии ветра.
Площадь, ометаемая крыльями ветроколеса:
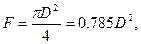
где D – диаметр ветроколеса.
При плотности воздуха r =1,23 кг/м³ мощность, развиваемую ветроколесом, можно определить по выражению
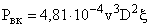 , кВт , кВт
| (2.12) |
Мощность, развиваемая с единицы ометаемой площади:
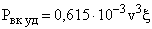 , кВт/м2. , кВт/м2.
| (2.13) |
Таким образом, мощность, развиваемая ветроколесом, определяется ометаемой площадью ветроколеса, скоростью ветра и величиной коэффициента использования энергии ветра.
Коэффициент использования энергии ветра
Ветроколесо преобразует в механическую энергию только часть полной энергии потока. Воздушный поток при прохождении через поперечное сечение, ометаемое ветроколесом, имеет приблизительно форму, показанную на рис. 2.1.
Скорость воздушного потока снижается по мере приближения его к ветроколесу и на некотором расстоянии за ним. По классической теории, полные потери скорости воздушного потока за ветроколесом в два раза больше, чем потери в плоскости вращения ветроколеса. Вместе с тем давление воздуха по мере приближения к ветроколесу повышается, а за ним оно резко падает, вследствие чего за колесом образуется некоторое разрежение.
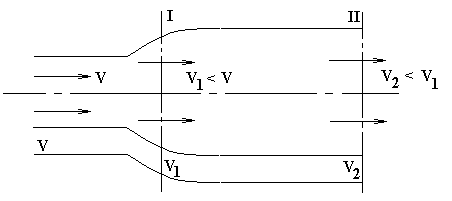
Рис.2.1. Изменение скорости ветра в плоскости вращения ветроколеса (I) и за ним (II)
Энергия, затраченная на вращение ветроколеса, равна разности кинетической энергии ветра перед ветроколесом и за ним:
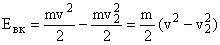
| (2.14) |
где v² – скорость воздушного потока за ветроколесом.
С другой стороны, воспринятую ветроколесом энергию можно выразить как произведение силы давления ветра G на скорость потока в плоскости ветроколеса:
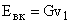 . .
| (2.15) |
Отношение энергии, воспринятой ветроколесом, к полной энергии, которой обладает воздушный поток, называется коэффициентом использования энергии ветра:
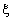 =Евк/Ев. =Евк/Ев.
| (2.16) |
Коэффициент использования энергии ветра зависит от величины потери скорости ветра при прохождении его через плоскость ветроколеса. Согласно классической теории ветроколеса
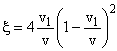
| (2.17) |
Н.Е.Жуковский для идеального ветроколеса установил максимальную величину коэффициента использования энергии ветра xmax = 0,593. Этот предел может быть получен при условии:
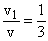 ,
,
т.е. идеальное ветроколесо должно работать так, чтобы потери скорости ветра в плоскости его вращения составляли 1/3 от поступающей величины.
Аэродинамические характеристики ветроагрегатов
Параметры различных ветроагрегатов удобно сопоставлять при помощи аэродинамических характеристик, которые показывают, как изменяются крутящий момент и коэффициент использования энергии ветра в зависимости от быстроходности ветроколеса. Необходимые данные для построения аэродинамических характеристик получают либо расчетом, либо экспериментально путем продувки модели ветроколеса в аэродинамической трубе. По полученным данным строят график, примерный вид которого показан на рис. 2.2.
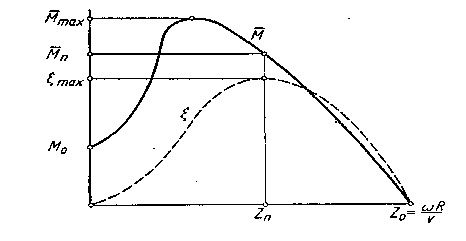
Рис.2.2 Аэродинамические характеристики ветроколеса.
По оси абсцисс откладывают значения быстроходности Z ветроколеса, которые выражаются отношением окружной скорости конца лопасти к скорости ветра:
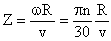 , ,
| (2.18) |
где w- угловая скорость, рад/c; R – радиус ветроколеса, м.
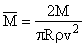 , ,
| (2.19) |
где М – момент, развиваемый ветроколесом.
Коэффициент использования энергии ветра определяется по выражению
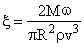 . .
| (2.20) |
Аэродинамическую характеристику строят в относительных величинах, поэтому она является общей для ветроколес любых размеров, если у них соблюдено геометрическое подобие. Основными точками кривой, определяющими главные параметры характеристики, являются:
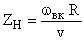 - номинальная быстроходность (число модулей), при которой коэффициент использования энергии ветра максимальный (xmax);
- номинальная быстроходность (число модулей), при которой коэффициент использования энергии ветра максимальный (xmax);
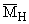 - номинальный относительный вращающий момент, который развивает ветроколесо при номинальном числе модулей ZН ;
- номинальный относительный вращающий момент, который развивает ветроколесо при номинальном числе модулей ZН ;
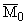 - начальный относительный момент, развиваемый колесом при трогании с места, т.е. когда Z = 0;
- начальный относительный момент, развиваемый колесом при трогании с места, т.е. когда Z = 0;
Z0 - синхронная быстроходность, при которой  =0;
=0;
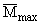 - максимальный момент, развиваемый ветроколесом; отношение (
- максимальный момент, развиваемый ветроколесом; отношение ( 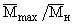 ) называется перегрузочной способностью ветроколеса.
) называется перегрузочной способностью ветроколеса.
Приведенные характеристики ветроколес различной быстроходности (рис.2.3), а также результаты теоретических и экспериментальных исследований позволяют сделать следующие выводы:
1. Чем больше число лопастей, их ширина и угол заклинивания, тем ниже быстроходность ветроколеса и кривая имеет крутопадающую форму.
2. Быстроходные ветроколеса развивают начальный момент М0, в несколько раз меньше номинального момента МН, а синхронная быстроходность в 2…2,5 раза выше номинальной.
3. Мощность ветроколеса, при прочих равных условиях, мало зависит от числа лопастей и коэффициента заполнения 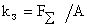 , представляющего собой отношение площади лопастей к ометаемой поверхности. Основное влияние оказывают форма и профиль лопастей, их положение в потоке воздуха и диаметр ветроколеса.
, представляющего собой отношение площади лопастей к ометаемой поверхности. Основное влияние оказывают форма и профиль лопастей, их положение в потоке воздуха и диаметр ветроколеса.
4. Снижение начального момента происходит быстрее, чем рост быстроходности. Так, при увеличении ZН в два раза М0 снижается в шесть-семь раз. В то же время приемистость, определяемая отношением М0/МH, у шестилопастного колеса в 3,3 раза выше, чем у двухлопастного.
5. Для постоянной аэродинамической схемы частота вращения ветроколеса прямо пропорциональна его быстроходности и скорости ветра и обратно пропорционально диаметру ветроколеса.
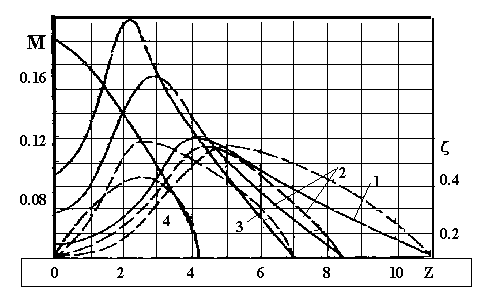
Рис.2.3. Характеристики ветроколес различной быстроходности:
1 –2-лопастного; 2 –3-лопастного; 3 –6-лопастного; 4 –18-лопастного;
сплошные линии M(Z); штриховые x(Z)
При выборе ветроагрегатов учитывают аэродинамические характеристики ветроколес и нагрузочные характеристики рабочих машин. Например, для привода тихоходной рабочей машины, имеющей большой начальный момент сопротивления, лучше использовать многолопастное тихоходное ветроколесо (ZН = 1,5…3). Это позволяет снизить значение минимальных рабочих скоростей ветра, уменьшить передаточное отношение редуктора и механические потери, но при этом снижается коэффициент использования ветра.
Для агрегатирования генератора, требующего большую частоту вращения и малый начальный момент, эффективнее использовать быстроходные ветроколеса (ZН = 5…8) с малым числом лопастей.
Для эффективного преобразования энергии ветра в зависимости от числа лопастей ветроколеса необходимо соответствующее оптимальное число модулей. Поэтому оптимальная быстроходность n-лопастного ветроколеса соответствует условию
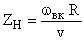 .
.
Например, для 2-лопастного ветроколеса коэффициент x будет максимальным при ZН = 4  /2=6, для 4-лопастного – при ZН =3.
/2=6, для 4-лопастного – при ZН =3.
Улучшить пусковые и рабочие характеристики ветроагрегатов можно несколькими методами (отключением нагрузки на период разгона ветроколеса, применением различных муфт, аэродинамических устройств). В быстроходных ветроагрегатах применяют автоматические системы управления поворотом лопастей.
Принцип работы ветроколеса
Ветроколесо, вращаясь под действием силы ветра, преобразует энергию ветра в механическую работу. Вращение ветроколеса обусловлено действием сил сопротивления или подъемной силы. Действие этих сил зависит от геометрии расположения лопастей.
Воздушный поток, обтекая ветроколесо, создает лобовое давление, называемое силой сопротивления. При этом величина силы сопротивления зависит от формы лопастей, состояния их поверхности и положения относительно направления воздушного потока.
На плоскость, расположенную перпендикулярно к потоку и двигающуюся по направлению ветра, действует воздушный поток силой RX. Под действием силы сопротивления ветроколесо приводится во вращение в плоскости, параллельной направлению ветра.
Для определения RX ее изучают в аэродинамической трубе. При этом вводятся соответствующие коэффициенты, с помощью которых от сил и моментов, действующих на модель, переходят к соответствующим силам и моментам, действующим на натурное тело (лопасти ветроколеса).
Сила сопротивления может быть определена выражением
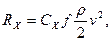 , ,
| (2.21) |
где СХ – коэффициент аэродинамической силы сопротивления; ƒ – площадь крыла.
Установлено, что сила сопротивления зависит от формы обтекающего тела, и тем она больше, чем больше завихрен поток, обтекающий тело, в частности, лопасти ветроколеса. Например, у вогнутого полого полушара СХ в 4 раза больше, чем у выпуклого.
На плоскость, расположенную под некоторым углом a к направлению воздушного потока, называемым углом атаки, действует некоторая сила R (рис.2.4). Эта сила раскладывается на две составляющие: сила RY действует вверх по вертикали и называется подъемной силой; сила RX создает лобовое давление и вызывает силу сопротивления.
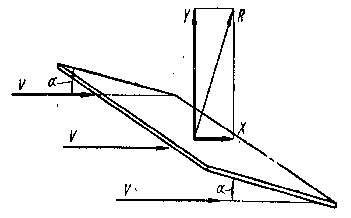
Рис.2.4. Подъемная сила, действующая на плоскость под углом атаки a
Подъемная сила выполняет полезную работу, приводя во вращение ветроколесо в плоскости, перпендикулярной направлению воздушного потока. Подъемная сила зависит от формы поперечного сечения крыла. Экспериментальные исследования в аэродинамической трубе позволили установить форму поперечного сечения крыла, которая дает наибольшую подъемную силу и наименьшую силу сопротивления. На рис. 2.5 для сравнения различных форм профиля показаны подъемные силы и силы сопротивления при одинаковом угле атаки. Наибольшую подъемную силу и наименьшую силу сопротивления имеет обтекаемый профиль
Обтекаемый профиль при малых углах атаки почти не вызывает вихрей, а пластинка вызывает значительные вихри на передней кромке. Вихри снижают подъемную силу и увеличивают силу сопротивления.
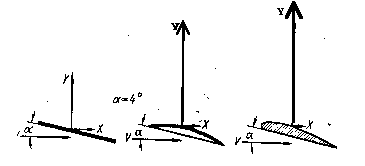
Рис. 2.5. Подъемная сила действующая на поверхности различного профиля
Подъемную силу можно определить по аэродинамическому коэффициенту СY:
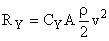 . .
| (2.22) |
Отношение коэффициента подъемной силы к коэффициенту силы сопротивления называется качеством крыла:
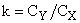 . .
| (2.23) |
Качество крыла у обтекаемых лопастей может достигать величины k=24 и более. Это значит, что подъемная сила лопасти при малых углах атаки в 24 раза больше силы сопротивления.
При взаимодействии воздушного потока с лопастью возникают:
1) сила сопротивления – параллельная направлению ветра;
2) подъемная сила – перпендикулярная силе сопротивления;
3) препятствие для набегающего потока. Это свойство характеризуется коэффициентом заполнения. Так, при одинаковой форме 4-лопастное колесо имеет вдвое больше геометрическое заполнение, чем 2-лопастное;
4) турбулизация потока, т.е. возмущение его скорости по величине и направлению как за колесом, так и перед ним. В результате лопасть часто оказывается в потоке, турбулизированном другими лопастями.
Таким образом, воздушный поток под действием силы сопротивления или подъемной силы приводит в движение ветроколесо. Полезное действие этих сил зависит от геометрии расположения ветроколеса и формы самих лопастей.
Дата добавления: 2016-03-15; просмотров: 4718;
