Перестановки, сочетания и размещенияЦель занятия;
Изучение понятий комбинаторики: факториала, перестановок, сочетаний и размещений. , Наработка навыков решения комбинаторных задач с применением формул перестановок, сочетаний и размещений.
1. Дидактическое оснащение практического занятия:
| Факториал n!=n(n−1)(n−2)(n−3)...3⋅2⋅1 Важно! | Факториал числа — это произведение натуральных чисел от 1 до самого числа(включая данное число). Обозначается факториал восклицательным знаком «!».
Например:
6!=  *6=720 6!=5!-6=120*6=720
5!=1*2*3*4*5=120 5!=4!*5=24*5=120
4!=1*2*3*4=24 4!=3!*4=6*4=24
3!=1*2*3=6 3!=2!*3=6
2!=1*2=2
1!=1
0!=1 *6=720 6!=5!-6=120*6=720
5!=1*2*3*4*5=120 5!=4!*5=24*5=120
4!=1*2*3*4=24 4!=3!*4=6*4=24
3!=1*2*3=6 3!=2!*3=6
2!=1*2=2
1!=1
0!=1
| ||||||
Размещения
Anm= 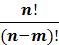 Размещения, это упорядоченные выборки
Размещения, это упорядоченные выборки
| Размещениемиз n элементов по m элементов (m≤n) называется упорядоченная выборка элементов m из данного множества элементов n.
| ||||||
| Перестановки Pn=n! | Перестановки — это специальный случай размещений, когда выборка так же велика, как данное множество. Размещения по n элементов из n называются перестановками из n элементов. Важно число перестановок, а не сами перестановки | ||||||
Перестановки с повторениями
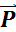 n= n=  Пример:
Сколько пятибуквенных слов можно составить из букв слова МАННА?
М- повторяется 1 раз
А- повторяется 2 раза
Н -повторяется 2 раза
Пример:
Сколько пятибуквенных слов можно составить из букв слова МАННА?
М- повторяется 1 раз
А- повторяется 2 раза
Н -повторяется 2 раза
 n=P2,2,1= n=P2,2,1= 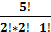 = = 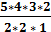 = 30 = 30
| Если в основном множестве k элементов a1,a2,...ak и выборка n элементов составляется так:
элемент a1 повторяется n1 раз,
элемент a2 повторяется n2 раз,
...
элемент ak повторяется nk раз,
такие выборки называются перестановками с повторениями.
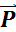 n=Pn1,n2,…nn= n=Pn1,n2,…nn= 
| ||||||
| Множества, подмножества, выборки | Конечным множеством называется множество, содержащее конечное число элементов. Подмножеством данного множества называется множество, все элементы которого принадлежат данному множеству. Пустое множество — это множество. не содержащее ни одного элемента. Выборками называются подмножества какого-либо множества. Упорядоченными выборками называются выборки, в которых важен порядок элементов. Если в выборке поменяют местами два элемента и получится другая выборка, то данная выборка является упорядоченной. Неупорядоченными выборками называются выборки, в которых не важен порядок элементов. | ||||||
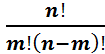
| Сочетанием из n элементов по m элементов (m≤n) называется выборка элементов m из данного неупорядоченного множества.
n показывает количество элементов данного множества
Сочетания из n элементов по m элементов получают, если из размещенийиз n элементов по m элементов исключаются те выборки, которые отличаются только порядком элементов. | ||||||
| Отличие сочетаний от размещений В размещениях порядок выборки важен В сочетаниях порядок выборки не важен | Размещения – это комбинации, в которых имеет значение порядок элементов . Размещения— это упорядоченные наборы. Сочетания- это комбинации, в которых важно знать только то, какие элементы выбраны, но их порядок не имеет значения. Сочетания не являются упорядоченными наборами |
Задания
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Задание №3 Цилиндр, вписанный в шар |
Дата добавления: 2016-03-15; просмотров: 1081;

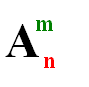 mпоказывает количество элементов размещения (сколько элементов выбирается)
n показывает количество элементов данного множества
mпоказывает количество элементов размещения (сколько элементов выбирается)
n показывает количество элементов данного множества