МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ

Магнитное поле – это форма материи, посредством которой осуществляется силовое взаимодействие движущихся электрических зарядов

(токов). С другой стороны само по себе магнитное поле создаётся движущими зарядами (токами). Этот факт был обнаружен экспериментально в опыте датского физика Ханса Эрстеда (рис. 1).

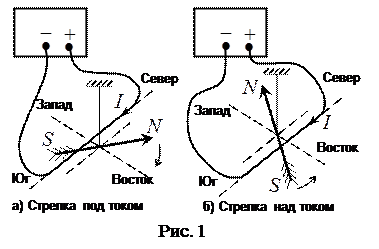В июле 1820 г. датский физик Ханс Эрстед открыл действие электрического тока на магнитную стрелку. “Гальваническое электричество, - писал он, - идущее с севера на юг над свободно подвешенной магнитной стрелкой, отклоняет её северный конец к востоку (рис. 1а), а, проходя в том же направлении под стрелкой, отклоняет её к западу” (рис. 1б).

В опытах Эрстеда был открыт новый вид взаимодействия. До сих пор физика знала лишь центральные силы. Провод же с током не притягивал и не отталкивал магнитной стрелки. Он лишь поворачивал её вокруг оси.

Таким образом, из опыта Эрстеда следует два фундаментальных вывода:

1. Магнитное поле создаётся движущимися зарядами (токами);

2. Магнитное поле действует на движущие заряды (токи).

Основной характеристикой магнитного поля является индукция 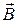- силовая характеристика, измеряемая в системе СИ в теслах (Тл).

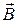Для наглядного изображения магнитного поля используются силовые линии (линии индукции). Силовой линией называется линия, в любой точке которой вектор направлен по касательной. Силовые линии магнитного поля являются замкнутыми и охватывают проводники с токами, что говорит о вихревом характере магнитного поля.

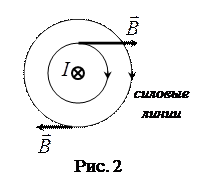
На рис. 2 изображено сечение проводника с током 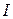, идущим перпендикулярно плоскости рисунка, и силовые линии этого проводника. Направление линий индукции связано с направлением тока правилом правого винта.

Основополагающим принципом магнетизма является принцип суперпозиции: индукция магнитного поля, создаваемая несколькими движущимися зарядами или токами является векторной суммой индукций, создаваемых отдельными движущимися зарядами или токами:

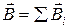, (1)

где 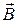- результирующая индукция, 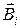- индукция слагаемых полей.

Экспериментально было установлено, что отдельный точечный заряд 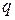, движущийся со скоростью 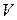, создаёт поле, индукция которого определяется формулой:

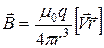. (2)

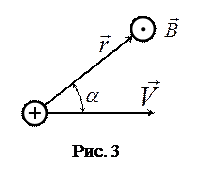Направление вектора 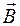связано правилом правого винта с векторам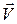и и 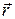(рис. 3). Вектор 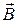направлен перпендикулярно плоскости, в которой лежат векторы 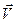и 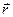(плоскость рисунка) и направлены «к нам», что обозначено точкой в кружке.

Модуль вектора 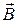из формулы (2) можно выразить так:

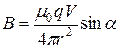, (3)

где 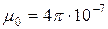Гн/м – магнитная постоянная, некий коэффициент в системе СИ. Кстати, все формулы электромагнетизма имеют разный вид в различных системах единиц. В нашей работе все формулы будут записываться в системе СИ без дальнейшего пояснения этого факта.

Опираясь на формулы (1), (2), (3), легко получить закон, определяющий магнитное поле отдельного элемента тока 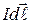, т.е. бесконечно малого отрезка проводника с током.

Будем исходить из принципа суперпозиции. Согласно этому принципу, магнитные поля отдельных движущихся зарядов складываются причём, каждый заряд создаёт магнитное поле, совершенно не зависимо от других зарядов.

В элементе тока 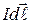имеется 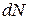одинаковых зарядов, движущихся с одной скоростью и в одном направлении. Число этих зарядов можно легко найти 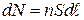, где 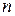- концентрация носителей, 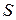- сечение проводника, 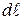- длина элемента.

Так как каждый заряд создаёт поле, индукция которого определяется формулой (2), то все 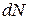зарядов создают поле в 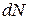раз большее, чем один заряд, т.е.:

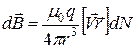
или

,

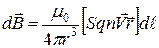где 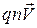- плотность тока 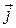, а произведение площади сечения на плотность тока:

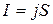- сила тока.

Учтём, что 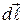и 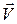однонаправлены и выразим эти векторы через их модули:

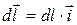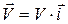и , где 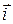- единичный вектор (орт) направления тока. Тогда:

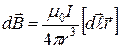. (4)

Эта формула выражает закон Био-Савара-Лапласа в векторной форме. В скалярной форме он выглядит так:

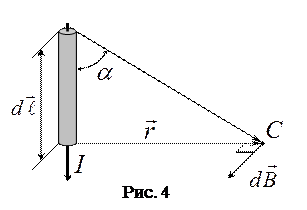
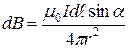, (5)

где 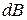- индукция магнитного поля, созданного элементом тока 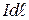, вектор 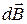направлен перпендикулярно плоскости рис. 4 «к нам», 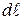- длина элемента, 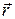- радиус-вектор, проведённый в точку, где определятся индукция, 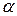- угол между элементом 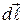и радиус-вектором.

Зная закон Био-Савара-Лапласа, и интегрируя его, можно получить поле любого тока. Это предлагается сделать студентам самостоятельно. В частности, для кругового проводника получаем такую формулу, определяющую индукцию в центре этой окружности:

,

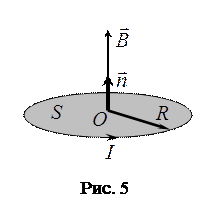
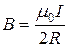где 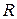- радиус окружности, которую образует проводник.

Для кругового проводника с током вводится понятие магнитного момента 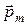. Магнитным моментом называется произведение силы тока в круговом контуре на площадь, ограниченную контуром (рис. 5):

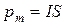. (6)

Введём единичный вектор (нормаль) 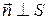, ( 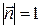) направление вектора 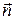связано с током правилом правого винта, тогда можно записать магнитный момент в векторной форме:

.

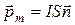Учитывая, что 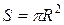, формулу (6) можно записать так:

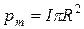. (7)

Обсудим далее вопрос о силовом действии магнитного поля.

Лоренц вывел формулу, определяющую силу воздействия магнитного поля на отдельный движущийся заряд, которая получила название силы Лоренца:

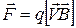(8)

или скалярно:

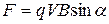, (9)

где 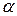- угол между векторам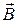и и .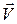

Из формул (8) и (9) видно, следующее:

1. Сила действует только на движущийся в магнитном поле заряд. При 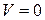, , 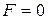т.е. сила не действует на неподвижный заряд.

2. Формула (8) показывает, что сила Лоренца перпендикулярна скорости заряда 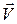, индукции магнитного поля 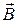, и связана правилом правого винта с 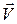и .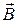

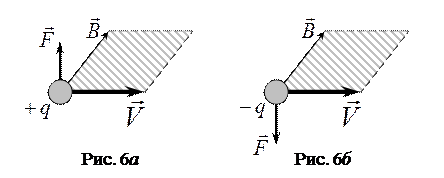
3. Направление силы Лоренца зависит от знака заряда (рис. 6а и 6б). В обоих случаях вектор силы 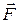перпендикулярен плоскост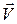и и 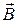, но направлен в разные стороны.

4. При 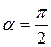, 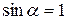сила Лоренца максимальна. Так как сила Лоренца перпендикулярна скорости 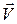, то она является центростремительной силой и заставляет частицу двигаться по окружности:

.

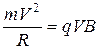При 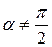частица движется по спирали. Уравнение движения частицы:

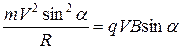
При 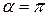, 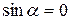сила Лоренца на частицу не действует.

В общем случае в пространстве имеют место и магнитное поле и электрическое, тогда сила Лоренца запишется так:

,

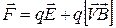где 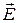- напряжённость электрического поля.

Применяя метод, использованный при выводе закона Био-Савара-Лапласа, из формулы (8) получим новый закон – закон Ампера, определяющий силу, действующую на элемент тока 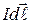в магнитном поле:

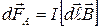
Или для прямолинейного проводника длиной 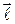в однородном магнитном поле :

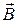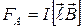. (10)

В скалярной форме формула (10) будет выглядеть так:

,

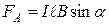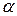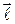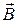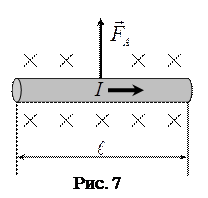
где - угол между и , направление же 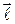определяется направлением тока в проводнике (рис.7).