МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ
Если в магнитное поле с индукцией 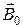 , созданное макротоками, внести вещество, то поле изменится. Это объясняется тем, что все вещества способны намагничиваться, т.е. приобретать магнитный момент и собственное магнитное поле
, созданное макротоками, внести вещество, то поле изменится. Это объясняется тем, что все вещества способны намагничиваться, т.е. приобретать магнитный момент и собственное магнитное поле 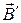 . В соответствии с принципом суперпозиции результирующее поле в магнетике определяется вектором
. В соответствии с принципом суперпозиции результирующее поле в магнетике определяется вектором
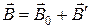 . (1)
. (1)
Под 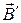 и
и 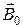 принимаются поля, усреднённые по физически бесконечно малому объёму.
принимаются поля, усреднённые по физически бесконечно малому объёму.
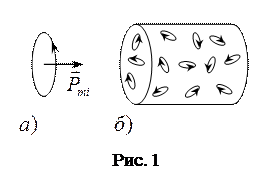 Установлено, что молекулы многих веществ обладают собственным магнитным моментом, обусловленным внутренним движением электрических зарядов. Каждому магнитному моменту соответствует элементарный круговой ток, создающий в окружающем пространстве магнитное поле (рис. 1а). При отсутствии внешнего магнитного поля магнитные моменты молекул ориентированы в пространстве беспорядочно, поэтому обусловленное ими результирующее магниевое поле равно нулю. Равен нулю и суммарный магнитный момент вещества (рис. 16).
Установлено, что молекулы многих веществ обладают собственным магнитным моментом, обусловленным внутренним движением электрических зарядов. Каждому магнитному моменту соответствует элементарный круговой ток, создающий в окружающем пространстве магнитное поле (рис. 1а). При отсутствии внешнего магнитного поля магнитные моменты молекул ориентированы в пространстве беспорядочно, поэтому обусловленное ими результирующее магниевое поле равно нулю. Равен нулю и суммарный магнитный момент вещества (рис. 16).
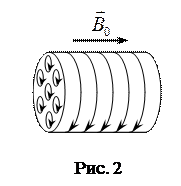 Во внешнем магнитном поле
Во внешнем магнитном поле 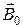 магнитные моменты молекул приобретают преимущественное ориентирование в одном направлении и вещество намагничивается. Магнитный момент вещества становится отличным, от нуля (рис. 2). При этом магнитные поля молекул уже не компенсируют друг друга, в результате возникает магнитное поле
магнитные моменты молекул приобретают преимущественное ориентирование в одном направлении и вещество намагничивается. Магнитный момент вещества становится отличным, от нуля (рис. 2). При этом магнитные поля молекул уже не компенсируют друг друга, в результате возникает магнитное поле 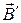 .
.
Степень намагничивания магнетика характеризуется магнитным моментом единицы объёма 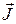 и называется намагниченностью:
и называется намагниченностью:
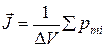 ,
,
где 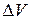 - физически бесконечно малый объём в окрестности данной
- физически бесконечно малый объём в окрестности данной
точки, 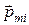 - магнитный момент отдельной молекулы. Суммирование проводится по всем молекулам в объёме
- магнитный момент отдельной молекулы. Суммирование проводится по всем молекулам в объёме 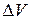 , Вещество намагничено однородно, если во всех его точках вектор
, Вещество намагничено однородно, если во всех его точках вектор 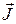 одинаков.
одинаков.
Индукция собственного поля магнетика 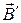 связана с намагниченность
связана с намагниченность 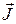 соотношением:
соотношением:
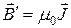 ,
,
где 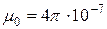 Гн/м – магнитная постоянная.
Гн/м – магнитная постоянная.
Тогда индукция суммарного магнитного поля вещества окажется
равной
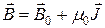 . (2)
. (2)
В этом случае для характеристики магнитного поля макротоков вводится более удобный вспомогательный вектор 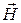 напряжённости магнитного поля:
напряжённости магнитного поля:
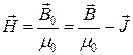 .
.
При этом формула (2) принимает вид:
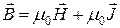 . (3)
. (3)
Для большинства магнетиков существует линейная зависимость намагниченности 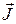 от напряжённости поля
от напряжённости поля 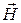 :
:
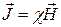 , (4)
, (4)
где 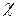 - магнитная восприимчивость, безразмерная величина, характерная для каждого данного магнетика.
- магнитная восприимчивость, безразмерная величина, характерная для каждого данного магнетика.
Если 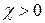 , т.е.
, т.е. 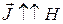 , вещества называются парамагнетиками. К ним можно отнести, например, платину, алюминий, воздух. Такие же вещества как висмут, медь, серебро, углерод имеют
, вещества называются парамагнетиками. К ним можно отнести, например, платину, алюминий, воздух. Такие же вещества как висмут, медь, серебро, углерод имеют 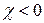 и называются диамагнетиками (для них
и называются диамагнетиками (для них 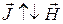 ).
).
Учитывая соотношение (4), выражение (3) для индукции суммарного поля в магнетике приводится к виду:
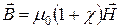 или
или 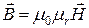 , (5)
, (5)
где 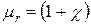 - относительная магнитная проницаемость вещества.
- относительная магнитная проницаемость вещества.
У парамагнетиков 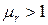 , диамагнетики имеют
, диамагнетики имеют 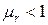 , причём как у тех, так и у других
, причём как у тех, так и у других 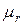 мало отличается от единицы, т.е. магнитные свойства этих магнетиков выражены очень слабо.
мало отличается от единицы, т.е. магнитные свойства этих магнетиков выражены очень слабо.
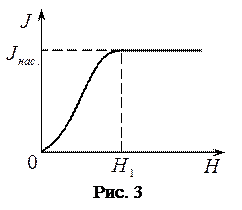 Помимо слабомагнитных веществ, существуют сильномагнитные - ферромагнетики. Типичные представители ферромагнетиков - железо, кобальт, гадолиний и многие их сплавы. Характерной особенностью ферромагнетиков является сложная нелинейная зависимость
Помимо слабомагнитных веществ, существуют сильномагнитные - ферромагнетики. Типичные представители ферромагнетиков - железо, кобальт, гадолиний и многие их сплавы. Характерной особенностью ферромагнетиков является сложная нелинейная зависимость 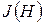 и
и 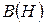 .
.
На рисунке 3 дана кривая намагниченности ферромагнетика. При напряжённости 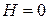 намагниченность ферромагнетика равна нули, её называют основной кривой намагничивания.
намагниченность ферромагнетика равна нули, её называют основной кривой намагничивания.
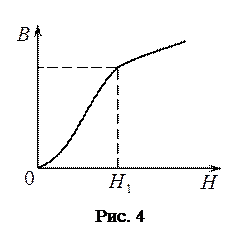 При сравнительно небольших значениях
При сравнительно небольших значениях 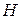 намагниченность
намагниченность 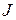 быстро растёт и достигает насыщения
быстро растёт и достигает насыщения 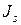 . Магнитная индукция
. Магнитная индукция 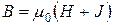 также растёт с увеличением
также растёт с увеличением 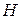 (рис. 4), а после достижения состояния насыщения
(рис. 4), а после достижения состояния насыщения 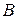 продолжает расти с увеличением
продолжает расти с увеличением 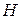 по линейному закону:
по линейному закону:
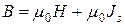 .
.
Ввиду нелинейной зависимости 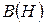 , для ферромагнетиков нельзя ввести магнитную проницаемость
, для ферромагнетиков нельзя ввести магнитную проницаемость 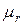 как определённую постоянную величину, характеризующую магнитные свойства каждого данного ферромагнетика. Однако по-прежнёму считается, что
как определённую постоянную величину, характеризующую магнитные свойства каждого данного ферромагнетика. Однако по-прежнёму считается, что
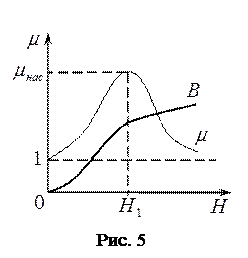
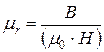 ,
,
при этом 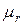 является функцией
является функцией 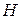 (рис. 5). Магнитная проницаемость
(рис. 5). Магнитная проницаемость 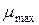 для ферромагнетиков может достигать очень больших значений. Так, например, для чистого железа – 5000, для сплава супермалой – 800000.
для ферромагнетиков может достигать очень больших значений. Так, например, для чистого железа – 5000, для сплава супермалой – 800000.
Для ферромагнетиков характерно также явление магнитного гистерезиса: связь между 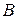 и
и 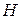 или
или 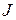 и
и  оказывается неоднозначной, а определяется предшествующей историей намагничивания ферромагнетика.
оказывается неоднозначной, а определяется предшествующей историей намагничивания ферромагнетика.
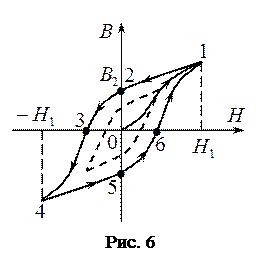 Если взять ферромагнетик с напряжённостью
Если взять ферромагнетик с напряжённостью 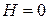 , и постепенно намагничивать, увеличивая
, и постепенно намагничивать, увеличивая 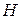 от нуля до некоторого значения, при котором наступает насыщение (точка 1 на рисунке 6), а затем, уменьшать напряжённость от
от нуля до некоторого значения, при котором наступает насыщение (точка 1 на рисунке 6), а затем, уменьшать напряжённость от 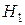 до
до 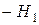 , то кривая намагничивания
, то кривая намагничивания 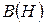 пойдёт не по первоначальному пути 01, а выше по пути 1234. Если изменять напряжённость
пойдёт не по первоначальному пути 01, а выше по пути 1234. Если изменять напряжённость 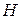 в обратном направлении от
в обратном направлении от 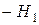 до
до 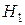 , то кривая намагничивания пройдёт ниже - по пути 4561.
, то кривая намагничивания пройдёт ниже - по пути 4561.
Получившаяся замкнутая кривая называется петлёй гистерезиса.
Из рисунка 6 видно, что при 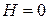 намагниченность не исчезает (точка 2) и характеризуется величиной
намагниченность не исчезает (точка 2) и характеризуется величиной 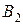 , называемой остаточной индукцией. С наличием такого остаточного намагничивания связано существование постоянных магнитов.
, называемой остаточной индукцией. С наличием такого остаточного намагничивания связано существование постоянных магнитов.
Величина 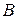 обращается в нуль (точка 3) лишь под действием
обращается в нуль (точка 3) лишь под действием 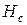 , имеющего направление, противоположное полю, вызвавшему намагничивание. Величина
, имеющего направление, противоположное полю, вызвавшему намагничивание. Величина 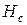 называется коэрцитивной силой. Значения
называется коэрцитивной силой. Значения 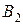 и
и 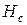 для разных ферромагнетиков меняется в широких пределах.
для разных ферромагнетиков меняется в широких пределах.
Физическую природу ферромагнетизма удалось понять только с помощью квантовой механики. При определённых условиях в кристаллах могут возникать, так называемые, обменные силы, которые заставляют спиновые магнитные моменты электронов устанавливаться параллельно друг другу. В результате возникают области (размером 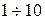 мкм) спонтанного, т.е. самопроизвольного, намагничивания – эти области называются доменами. В пределах каждого домена ферромагнетик намагничен до насыщения и имеет определённый магнитный момент. Направление этих моментов для разных доменов различны, поэтому при отсутствии внешнего поля суммарный момент образца равен нулю и образец в целом представляется макроскопически не намагниченным.
мкм) спонтанного, т.е. самопроизвольного, намагничивания – эти области называются доменами. В пределах каждого домена ферромагнетик намагничен до насыщения и имеет определённый магнитный момент. Направление этих моментов для разных доменов различны, поэтому при отсутствии внешнего поля суммарный момент образца равен нулю и образец в целом представляется макроскопически не намагниченным.
При включении внешнего магнитного поля домены, ориентированные по полю, растут за счёт доменов, ориентированных против поля. Такой рост в слабых полях имеет обратимый характер. В более сильных полях происходит одновременное переориентирование магнитных моментов в пределах всего домена. Этот процесс является необратимым, что и служит причиной гистерезиса и остаточного намагничивания.
При нагревании ферромагнетика тепловое движение разрушает магнитный порядок в доменах и при температуре 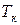 , называемой точкой Кюри, ферромагнетик скачком теряет свои свойства и превращается в обыкновенный парамагнетик. Например, для железа
, называемой точкой Кюри, ферромагнетик скачком теряет свои свойства и превращается в обыкновенный парамагнетик. Например, для железа 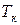 = 768°С.
= 768°С.
Дата добавления: 2016-03-10; просмотров: 1376;
