Из (5.11) следует, что

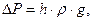
Тогда потери давления будут

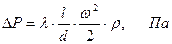(5.13)

Если скорость w выразить через объемный расход и площадь сечения из уравнения (5.1)

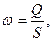(5.14)

то уравнение (5.12) примет вид:

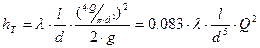(5.15)

В наклонном трубопроводе:

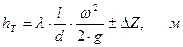(5.16)

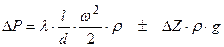(5.17)

+ - когда сумма участков подъема по высоте больше суммы участков спуска;

- - когда наоборот.

где l – длина трубопровода, м;

d - внутренний диаметр, м;

ρ - плотность жидкости, кг/м³;

ΔZ - разность геодезических отметок начала и конца трубопровода, м;

G - ускорение силы тяжести, м/с²;

λ - коэффициент гидравлического сопротивления, который в общем случае зависит от числа Рейнольдса Re и относительной шероховатости стенки трубопровода

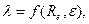(5.18)

где ε– относительная шероховатость.

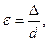(5.19)

где Δ – абсолютная эквивалентная шероховатость выбирается по таблице, мм;

d - внутренний диаметр трубы, мм.

Абсолютная эквивалентная шероховатость – это такая высота шероховатости, при которой в квадратичной зоне сопротивления потери напора равны потерям напора для данной естественной шероховатости трубы.

Для ламинарного режима движения (Rе < Rекр) коэффициент гидравлического сопротивления зависит только от параметра Рейнольдса:

Rе_кр = 2320

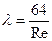(5.20)

Если учесть, что

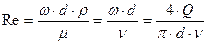(5.21)

и подставить выражение (79) в (78), то получим

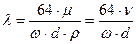(5.22)

В этом случае выражение (70) принимает вид формулы Пуазейля:

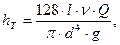(5.23)

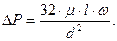(5.24)

При турбулентном режиме движения (Rе > Rе_кр) различают три зоны сопротивления.

1. Зона гидравлически гладких труб ( ) :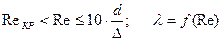

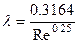- (5.25)

формула Блазиуса, используемая при Rе ≤ 10⁵. Здесь сопротивление шероховатых и гладких труб одинаково.

В зависимости от скорости течения и вязкости жидкости одна и та же труба может быть гидравлически гладкой и гидравлически шероховатой.

2. Зона шероховатых труб или смешанного трения

( ):

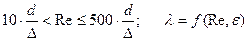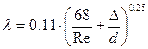- (5.26)

формула Альтшуля.

3. Зона вполне шероховатых труб или квадратичная зона

):

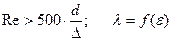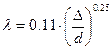(5.27)

- формула Шифринсона.

Для нефтепроводов наиболее характерны режимы гладкого или смешанного трения.

Разновидностью формулы Дарси-Вейсбаха, часто применяемой при технологических расчетах трубопроводов, является формула академика Лейбензона:

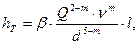(5.28)

где Q и ν - соответственно объемный расход и кинематическая вязкость перекачиваемой жидкости;

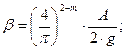
β, А, m- коэффициенты, зависящие от режима течения жидкости.

Формула (5.28) в явной форме выражает зависимость h от Q и получается из выражения (5.12) при условии, что λ определяется выражением вида

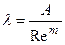. (5.29)

Формулы для расчета коэффициента гидравлического сопротивления в зависимости от режима течения приведены в табл. 5.1.

Потеря напора на единицу длины трубопровода называется гидравлическим уклоном:

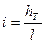. (5.30)

Для наглядности и представления о гидравлическом уклоне сделаем построение гидравлического треугольника: отложим от начальной А' и конечной B' точек на профиле трассы трубопровода статические (пьезометрические) напоры 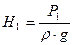и и 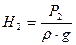концы полученных отрезков соединим прямой AB. Эта прямая называется линией падения напора или линией гидравлического уклона. Она показывает характер распределения напора по длине трубопровода.

Из построения следует, что гидравлический уклон является тангенсом угла наклона этой прямой к горизонту:

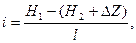(5.31)

то есть i = const.

Величина 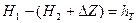и характеризует потери напора на трение в трубопроводе и показывает, что разность статических напоров целиком затрачивается на преодоление гидравлических сопротивлений, возникающих при течении жидкости по трубопроводу.

Таблица 5.1. Формулы для расчета коэффициента гидравлического сопротивления

Ламинарный режим	Турбулентный режим
Re < 2320	Зона Блазиуса	Переходная зона	Автомодельная зона
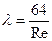
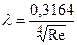
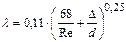
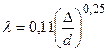
Зона гидравлически гладких труб	Зона гидравлически шероховатых труб
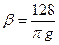
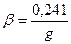
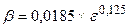
m = 1	m = 0,25	m = 0,125	m = 0

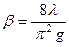
Перед началом гидравлического расчета исследуется профиль трассы трубопровода для определения на нем перевальных точек и нахождения его расчетной длины. Эта длина может быть значительно меньше геометрической, а перевальная точка не обязательно является наивысшей точкой трассы. Достаточно закачать жидкость на перевальную точку, чтобы она самотеком достигла конца трубопровода.