ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ

В зависимости от полноты охвата объекта различают сплошное и несплошное наблюдение. Одним из видов несплошного наблюдения является выборочное. Выборочным наблюдением называют обследование отобранного в случайном порядке определенного числа единиц совокупности с целью получения обобщающих характеристик всей совокуп­ности.

В настоящее время выборочное наблюдение нашло широкое при­менение, так как этот вид наблюдения имеет теоретическое обоснова­ние и ряд преимуществ перед сплошным наблюдением:

1) выборочное наблюдение применяется в тех случаях, когда сплошное вообще невозможно:

— исследование может быть связано с уничтожением или пор­чей обследуемых единиц, например при контроле качества хлебобулочных изделий, проверке ткани на прочность и т.д. При выборочном наблюдении порча и уничтожение обсле­дуемых объектов сводится к минимуму,

— обследуемая совокупность велика, практически безгранич­на, например совокупность колосьев пшеницы в поле;

2) выборочное наблюдение используется для исследования про­цессов, сплошное наблюдение которых нецелесообразно, например бюджетные обследования, изучение потребительского спроса и др.;

3) основное достоинство выборочного наблюдения в том, что ско­рее, проще и дешевле обследовать часть, чем целое. Изучение стати­стических совокупностей, состоящих из множества единиц, связано с большими трудовыми и материальными затратами. В силу сокраще­ния объема работ по сбору и обобщению данных происходит эконо­мия трудовых, материальных и денежных ресурсов, сокращаются сро­ки получения конечных результатов обследования;

4) при выборочном наблюдении достигается большая точность результатов благодаря сокращению ошибок, происходящих при реги­страции;

5) выборочное наблюдение может применяться для уточнения результатов сплошного наблюдения. Например, при проведении переписи иногда организуют выборочные контрольные обходы;

6) для изучения очень больших совокупностей более точные результаты может дать выборочное наблюдение, чем сплошное, и, кроме того, выборочную совокупность можно изучить более тщательно.

Цель проведения выборочного наблюдения состоит в том, чтобы по характеристикам отобран­ной части единиц судить о характеристиках всей совокупности. Если выборочное наблюдение проведено с соблюдением всех требований научной организации, то данные выборки будут более точно характе­ризовать всю совокупность, в противном случае возможны значитель­ные расхождения.

Выборочное наблюдение состоит из следующих этапов:

1) постановка цели и формулировка задач наблюдения;

2) составление программы наблюдения и разработка ее материа­лов;

3) решение организационных вопросов наблюдения;

4) определение объема выборки и способа отбора;

5) непосредственное проведение отбора, т.е. процесс образования выборочной совокупности;

6) регистрация соответствующих признаков у отобранных единиц;

7) обобщение данных наблюдения и расчет выборочных характе­ристик;

8) определение ошибок выборки;

9) распространение (пересчет) выборочных данных на всю сово­купность.

Этапы 1, 2, 3 и 6 выборочного наблюдения осуществляются так же, как и при сплошном наблюдении.

Отбор единиц совокупности должен быть случайным, т.е. таким, чтобы обеспечивал каждой единице одинаковую возможность быть отобранной.

Равенство шансов попадания в выборку для каждого наблюде­ния, т.е. отбор наугад, гарантирует, что в таком отборе не будет наме­ренных или ненамеренных искажений, поэтому наилучшей моделью отбора считается вероятностная, или случайная, выборка, в которой строго соблюдается принцип равенства шансов попадания в выборку для всех единиц изучаемой совокупности.

Совокупность объектов, из которой производится отбор, при­нято называть генеральной, и все ее обобщающие показатели называ­ют генеральными.

Различают идеальную и реальную генеральную совокупности. Идеальная генеральная совокупность, задаваемая теоретическим опи­санием предмета исследования, является теоретической абстракцией, она почти никогда полностью не совпадает с реальной генеральной совокупностью, которая подвержена постоянным колебаниям. Реальная генеральная совокупность получается путем исключения из иде­альной совокупности всех труднодоступных единиц наблюдения.

Выборочную совокупность (выборку) формируют из реальной генеральной совокупности, и все ее обобщающие показатели называют выборочными. Выборка — это подмножество заданной совокупности, позволяющее делать более или менее точные выводы относительно совокупности в целом. Следовательно, выборочная совокупность выступает и как объект обследования, и как средство получения им формации о генеральной совокупности. При правильной организации выборочного наблюдения выборочные показатели очень близки к ге­неральным. Это следует из закона больших чисел.

Статистической оценкой или статистикой характеристики (па­раметра) генеральной совокупности называют приближенное значение искомой характеристики (параметра), полученное по данным выборки. В статистике используются два вида оценок — точечные и интерваль­ные.

Точечной статистической оценкой параметра генеральной совокуп­ности называется конкретное числовое значение искомой характери­стики. Интервальная оценка представляет собой числовые интерва­лы, предположительно содержащие значение параметра генеральной совокупности.

Качество статистических оценок определяется следующими их свойствами:

— состоятельность. Оценка считается состоятельной, если при не­ограниченном увеличении объема выборки ее ошибка стремится к 0;

— несмещенность. Оценка считается несмещенной, если при данном объеме выборки п среднее значение ошибки равно 0;

— эффективность. Оценка считается эффективной, если ее ошиб­ка, называемая ошибкой выборки, является величиной минимальной.

В процессе проведения выборочного наблюдения появляются ошибки, которые можно разде­лить на две группы:

1) ошибки регистрации;

2) ошибки репрезентативности (представительства).

При любом наблюдении могут происходить ошибки регистрации, которые появляются в связи с неправильным установлением факта в процессе наблюдения. Они могут возникать из-за сообщения оши­бочных сведений, ошибок в фиксации предоставленных сведений, не­точного подсчета фиксируемых признаков и т.д.

Ошибки регистрации имеют два вида: случайные и систематиче­ские. Случайные ошибки регистрации — это неумышленные неточно­сти при фиксации признаков. Поэтому при обобщении большого чис­ла данных случайные ошибки регистрации взаимопогашаются и не вызывают больших искажений обобщающих характеристик. Система­тические ошибки регистрации вызваны односторонним (преднамерен­ным или непреднамеренным) искажением фиксируемого признака, такие ошибки не погашаются, а накапливаются и приводят к существенному преувеличению или преуменьшению обобщающих харак­теристик.

Ошибок регистрации можно избежать, если правильно организовать проведение наблюдения. Этот вид ошибок свойственен и сплошному и выборочным наблюдениям, но, как отмечалось ранее, ошибки регистрации при выборочном методе значительно сокращаются, так исследуется только часть совокупности.

При выборочном наблюдении появляются ошибки, которых нет при сплошном обследовании — это ошибки репрезентативности (ошибки выборки). Ошибка репрезентативности — это мера отклонения статистической структуры выборки от структуры соответствующей генеральной совокупности. В связи с этим обобщающие характеристики выборки более или менее существенно отличаются от обобщающих характеристик всей совокупности. Избежать ошибок репрезентатив­ности нельзя, но если соблюдать требования к проведению выборочного обследования, то их можно свести к минимуму.

Неконтролируемые перекосы в распределении выборочных на­блюдений могут быть вызваны: 1) заменой требуемых единиц наблю­дения другими, более доступными; 2) неполным охватом выборочной совокупности. Соответственно ошибки выборки можно подразделить на два вида — систематические (тенденциозные) и случайные.

Систематические ошибки являются результатом деятельности самого исследователя. Они появляются в том случае, когда нарушено первое требование проведения выборочного наблюдения, т.е. случай­ный отбор. Это приводит к тому, что выборочное наблюдение теряет всякий смысл, поскольку на его основе нельзя правильно судить о по­казателях всей совокупности.

Систематические ошибки возникают, когда: 1) выборка не соот­ветствует задачам исследования; 2) не изучен характер генеральной совокупности; 3) отбираются только «выигрышные» элементы гене­ральной совокупности, например только лучшие или худшие единицы. Предположим, что средний ежемесячный семейный доход пен­сионеров в генеральной совокупности составляет 3 тыс. руб., а по ре­зультатам выборочных обследований получили 6 тыс. руб. Это озна­чает, что была опрошена только часть более обеспеченных пенсионеров. Следовательно, в исследование вкралась ошибка репрезентативности. Систематические ошибки при возрастании объема выборки не уменьшаются. Их можно уменьшить только соблюдением принципа случайного отбора, при котором все объекты имеют одинаковую веро­ятность попадания в выборку.

Закон больших чисел обосновывает применение выборочных наблю­дений в статистике. Если принцип случайного отбора не соблюдается, то применять теоремы закона больших чисел нельзя, так как эти теоремы выведены из закономерностей, возникающих в случайном процессе.

Если принцип случайного отбора соблюдается, то ошибки выбор­ки носят случайный характер, т.е. имеют равную возможность в одинаковой степени преуменьшать или преувеличивать характеристики генеральной совокупности. Случайные ошибки появляются в том случае, когда нарушено второе требование к проведению выборочного исследования, т.е. для исследования было отобрано недостаточное количество единиц совокупности. Например, во время проверки качества подготовки студентов для обследования была отобрана только одна группа.

Случайные ошибки возможны и при совершенно правильном отборе за счет того, что случайно могут оказаться отобранными единицы с характеристиками, в среднем отличными от всей совокупности.

Закономерности изменения случайных ошибок изучает теория больших чисел, которая доказывает, что с увеличением объема выбор­ки размеры случайных ошибок сокращаются.

Таким образом, для уменьшения ошибки выборки, необходимо, чтобы:

— выборка формировалась из однородной совокупности;

— были изучены характеристики генеральной совокупности;

— каждая единица генеральной совокупности имела равную ве­роятность попадания в выборку;

— объем выборки должен иметь достаточное количество единиц.

Уменьшение ошибок выборки называется контролированием реп­резентативности.

Ошибку выборки определяют как рас­хождение между оценкой некоторого показателя, получаемой на ос­новании исследования выборки, и истинным значением этого показа­теля в генеральной совокупности.

На практике ошибка выборки определяется отклонением сред­них характеристик выборочной совокупности от средних характери­стик генеральной совокупности.

Разница статистических характеристик генеральной и выборочной совокупности называется ошибкой выборки или репрезентативности и обозначается

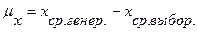
где хср.генер. и хср.выбор. - соответственно генеральная и выборочная средние.

Ошибка выборки зависит от объема выборки и от степени варьи­рования признака, т.е. от среднего квадратического отклонения. Учет объема выборки и варьирования признака находит выражение в формулах средней ошибки выборки.

Величина ошибки выборки средней 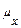зависит от числа наблюдений составляющих выборочную совокупность и дисперсии изучаемого признака 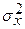. Чем больше величина выборки n тем ошибка выборки меньше. Чем больше дисперсия значений признака в выборке 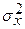тем больше ошибка выборки. Аналитически это записывается так:

,

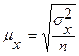Дисперсию доли, как альтернативного признака, определяют по формуле

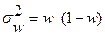
где w - доля

Соответственно, ошибка доли определяется по формуле

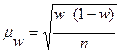
В математической статистике доказано, что с определенной вероятностью р можно утверждать, что при данной дисперсии изучаемого признака и числа наблюдений величина ошибки выборки не превысит определенной заранее заданной величины, называемой предельной ошибкой выборки .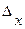

Предельную ошибку средней определяют по формуле

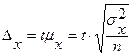
где t - коэффициент доверия (отношение предельной и средней ошибки выборки).

Коэффициент доверия определяется по выписке из таблицы значений функции приведенную в конце настоящих методических указаний.

Предельную ошибку доли определяют по формуле:

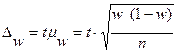
В зависимости от способа отбора единицы в выборочную совокупность различают следующие виды выборки:

индивидуальную, серийную;

случайную, механическую, типологическую;

повторную, бесповторную;

При бесповторной выборке единица изучаемого явления может попасть в выборку только один раз, при повторном способе отбора единица изучаемого явления может попасть в выборку нескольких раз. Соответственно, ошибка выборки при бесповторном отборе рассчитывается по формуле:

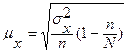
где N - число единиц в генеральной совокупности:

при повторном отборе - по формуле

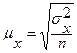
Задаваясь определенной допустимой ошибкой выборки 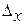с вероятностью ошибки р и зная дисперсию изучаемого признака 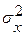определяют число единиц n подлежащих отбору в выборочную совокупность при бесповторном отборе:

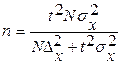
при повторном отборе:

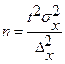
Отбор при выборочном наблюдении — это процесс образования выборочной совокупности. Отбор единиц из генеральной совокупности в выборку может быть осуществлен по-разному. В зависимости от ряда условий (сущности явления, объема совокупности, вариации и распределения наблюдаемых признаков и др.) выбирают наиболее предпочтительную систему организации отбора единиц из генеральной совокупности.

Система организации отбора выборки определяется методом, видом и способом отбора. В зависимости от того, участвуют ли ото­бранные единицы в дальнейшей выборке или нет, различают два ме­тода отбора: повторный и бесповторный.

В зависимости от характера единицы отбора повторный и беспов­торный методы применяются в сочетании с различными видами отбо­ра. В практической деятельности различают следующие виды отбора:

— индивидуальный — отбор отдельных единиц из генеральной совокупност

— групповой — отбор целых групп единиц или серий;

— комбинированный — комбинация группового и индивидуаль­ного видов. При комбинированном отборе отбираются группы единиц совокупности, а затем обследуется только часть единиц из отобран­ных групп.

Достоверность рассчитанных по выборочным данным характери­стик в значительной мере определяется репрезентативностью выбороч­ной совокупности, которая зависит от способа отбора единиц из гене­ральной совокупности. Различные виды отбора могут осуществляться разными способами формирования выборочной совокупности. Все применяемые способы отбора можно разделить на две группы:

1) способы, при которых отбор производится без предваритель­ного деления генеральной совокупности на группы. К данной группе относится собственно-случайный отбор;

2) способы, при которых отбор производится после выделения в генеральной совокупности ее частей. К данной группе относятся сле­дующие способы:

— механический (систематический),

— районированный (стратифицированный), разновидностью которого является типический отбор,

— серийный (гнездовой, кластерный).

В зависимости от того, как изменяется единица отбора, при по­следовательном проведении ряда выборок различают одноступенча­тый и многоступенчатый отбор.

В зависимости от принципа случайности выборки делятся на два класса (случайные и неслучайные), каждый из которых подразделяет­ся на несколько видов (типов):

— к случайным выборкам относят: 1) собственно-случайную; 2) механическую; 3) районированную; 4) серийную;

— неслучайным выборкам относят: 1) стихийную; 2) метод основ­ного массива; 3) квотную.

Собственно-случайный отборпроизводится из всей массы еди­ниц генеральной совокупности. В данном случае отбор осуществляет­ся наугад, при этом каждой единице совокупности обеспечивается оди­наковая вероятность быть отобранной благодаря случайности.

Механический (систематический) отборприменяется в тех слу­чаях, когда имеется объективная последовательность в расположении единиц отбора, т.е. генеральная совокупность каким-либо образом упорядочена. Механическим называется такой отбор единиц, который производится механически через определенный интервал. Например, если выборка должна составлять 50% генеральной совокупности, то отбирается каждый второй элемент генеральной совокупности. Меха­нический отбор еще называют систематическим, а в иностранной ли­тературе — псевдослучайным.

Районированный (стратифицированный) отборпроизводится из предварительно расчлененной на непересекающиеся районы (страты — слой, пласт) или группы генеральной совокупности. Данный способ отбора используется при изучении сложных совокуп­ностей, когда генеральная совокупность велика или неоднородна, а так­же тогда, когда из каких-то содержательных соображений важно обес­печить представительность выборки по конкретным важным для исследовательских целей критериям. В этих случаях генеральную со­вокупность разделяют на более или менее однородные части, а затем осуществляют отбор единиц внутри этих частей.

В качестве групп в зависимости от характера генеральной совокуп­ности могут использоваться области, отрасли предприятий, отдельные предприятия, группы населения и т.д. Если деление происходит по стратам (социальным группам), то выборку именуют стратифицированной, если по экономико-географическим районам, то — районированной.

В отдельных случа­ях целесообразно проводить отбор не отдельных единиц, а целых групп (серий, гнезд) с тем, чтобы в таких группах подвергать наблюдению все без исключения единицы, т.е. осуществляется сплошное наблюде­ние. Проводить такой отбор целесообразно в том случае, если обсле­дуемый признак колеблется в различных сериях незначительно.

Серийный отбор заключается в том, что генеральную совокуп­ность разбивают на некоторое число непересекающихся серий и по схеме случайного отбора с возвратом или без возврата контролируют все элементы лишь отобранных серий. В данном случае серии как бы составляют большую единицу отбора. Например, при изучении про­изводительности труда в качестве единицы отбора может выступать не отдельный рабочий, а вся производственная бригада.

Комбинированная выборка предпола­гает использование нескольких способов выборки. Если способы от­бора применяются в комбинации, то такой отбор называется комбини­рованным. Например, можно комбинировать типическую и серийную выборки, когда серии отбираются в установленном порядке из несколь­ких типических групп.

Отборы могут быть одно- и многоступенчатыми. Отбор называется одноступенчатым, если отобранные каким-6о способом единицы подвергаются наблюдению, и по ним делаются обобщения.

Большинство крупных выборочных обследований производится на основе одного способа отбора, а сочетают два или более способов, образующих ступени отбора.

Многоступенчатый отбор предполагает извлечение из генераль­ной совокупности сначала укрупненных групп единиц, а затем групп, меньших по объему, и так до тех пор, пока не будут отобраны те груп­пы (серии) или отдельные единицы, которые будут подвергнуты на­блюдению. Другими словами, многоступенчатый отбор предполагает подвыборку, которая заключается в отборе более мелких единиц из уже отобранных крупных.

Многоступенчатая выборка может состоять из нескольких сту­пеней, но чаще всего встречается ее двухступенчатая форма. Способы отбора на отдельных ступенях могут изменяться. Схема многоступен­чатого отбора должна выбираться только после предварительного изу­чения структуры генеральной совокупности. Обычно объект и круг обследования определяются уже на первой ступени. Данные, получае­мые относительно первичных более крупных единиц, могут содержать в себе информацию и об элементарных единицах.

Когда выборочные совокупности образуются так, что одни сведения собираются от всех единиц отбора, затем отбираются еще некоторые единицы и обследуются по более широкой программе, то такая выборка называется многофазной (двухфазной трехфазной, четырехфазной и т.д.).

В простейшем случае многофазная выборка состоит из двух фаз случайного отбора. На первой — как при серийном отборе — выбира­ются первичные единицы отбора, например районы, дома, избиратель­ные участки. На второй фазе производится случайный отбор единич­ных членов генеральной совокупности—отдельных респондентов, семей и т.п.

Так как первичные единицы отбора могут существенно отличать­ся по величине (например, отличаются друг от друга дома с разной численностью проживающих), то результатом первой фазы может стать неравная вероятность попадания в выборку для членов генеральной совокупности, относящихся к разным первичным единицам отбора. В этом случае исследователь имеет возможность выравнивания веро­ятностей на последующих фазах, например, из первичной единицы отбора, где проживает 1000 семей, он выберет 10, а из первичной еди­ницы отбора, где живет 500 семей, будет отобрано 20.

Отличие многофазной выборки от многоступенчатого отбора за­ключается в том, что при многофазной выборке на каждой фазе про­изводится обследование отобранных единиц и всегда сохраняется одна и та же единица отбора. В многоступенчатых выборках единица отбо­ра на каждой ступени выборки различна и обследуются только едини­цы, отобранные на последней ступени.

Многофазная выборка может быть связана с многоступенчатой выборкой. На каждой отдельной ступени многоступенчатая выборка может быть многофазной. Например, земские статистики в разное вре­мя обследовали состояние крестьянских хозяйств по различным про­граммам. По узкой программе производилось наблюдение всех хо­зяйств, по расширенной программе — каждого пятого, по более широкой — каждого десятого, по подробной — каждого двадцатого хо­зяйства. В этом случае получаем не многоступенчатую, а многофаз­ную выборку.

Взаимопроникающие выборки применяют тогда, когда необходимо быстро получить предварительные итоги при выборочных обследованиях. Такие выборки можно получить разным обследователям, что позволяет делать сопоставления итогов по всем частям и обеспечить взаимную проверку их работы. Если несколько выборок приводят к сходным результатам, то это свидетельствует о том, что истинные ве­личины и соотношения репрезентативны достаточно точно. Но для того чтобы такая возможность сравнения действительно существовала, не­обходима полная идентичность условий, в которых проводится эта выборка. Все различия в характере объектов отбора или в среде, в ко­торой эти объекты находятся, делают несопоставимыми результаты работы. Необходимо, чтобы выборочные совокупности, образованные как взаимопроникающие выборки, действительно представляли собой извлечения из одной общей совокупности.

К группе неслучайных способов отбора относятся стихийный, метод основного массива, квотный. Сти­хийный отбор внешне похож на вероятностный, случайный. Однако никаких математических процедур при формировании выборки не применяется, и поэтому соблюсти контроль за обеспечением репрезентативности невозможно.

К стихийному отбору тесно примыкает метод основного массива. Процедура его проста: из жителей данного района или работников предприятия опрашивается простое большинство. В результате сред­ние генеральной и выборочной совокупностей сближаются, а выбороч­ная совокупность составляет преимущественную часть генеральной и перекрывает возможное смещение.

Квотный отбор основан на целенаправленном формировании структуры выборочной совокупности. Идея квотной выборки заклю­чается в том, что изучаемая совокупность разбивается на такие соци­ально-демографические группы, которые исследователь по определен­ным причинам считает важными. Обычно критериями разбивки становятся пол, возраст, национальная принадлежность, место житель­ства и т.п.

РЯДЫ ДИНАМИКИ

Общественные явления претерпевают непрерывные изменения во времени. В процессе исторического развития изменяются их объем уровень, состав и др., т.е. общественные явления изменяются как ко­личественно, так и качественно. Это происходит в результате влияния на них многих факторов социального, экономического, технического характера. Особенно подвижна количественная сторона общественной жизни, поэтому, чтобы правильно понять явление, статистика изучает его в развитии, и на основе этого изучения решает вопрос о перспекти­вах развития. Процесс развития, движение общественных явлений во времени называется динамикой.

Для изучения динамики строят ряды динамики (или временные,
хронологические ряды). Ряд динамики представляет собой ряд изме­няющихся во времени значений какого-либо показателя, расположен­ных в хронологическом порядке.

Ряды динамики состоят из двух элементов:

1) время (t). В качестве показателя времени выступают либо оп­ределенные даты (моменты), либо отдельные периоды времени (годы> кварталы, месяцы, недели, сутки);

2) уровень (у). Уровнем называется каждое отдельное числовое значение показателя, характеризующее величину явления за отдельный период либо на момент времени. Уровни рядов динамики дают количественную оценку (меру) развития во времени изучаемого явления.

Каждый динамический ряд состоит из п-го числа варьирующих _{0 в}ремени значений показателя. Обычно первый член ряда называют начальным уровнем и обозначают у₀ или у,, а последний — конечным обозначают уn. В качестве обобщенной характеристики значений по­казателя, изменяющегося во времени, служит средний уровень ряда (у). Уровни ряда динамики обладают следующими особенностями:

1) уровень последующего времени зависит от уровня, достигну­того в предыдущее время;

2) чем больше интервал времени между событиями, тем больше различаются их количественное и качественное состояние.

Ряды динамики, как правило, представляют в виде таблиц или графически. При графическом изображении динамического ряда на оси абсцисс строится шкала времени, а на оси ординат — шкала уров­ней ряда. На одной координатной сетке можно разместить несколько кривых, каждую из которых выделяют цветом или рисунком (сплош­ная, пунктирная и другие линии). Следует иметь в виду, что изобра­жение большого числа кривых приводит к потере наглядности.

Существуют различные виды рядов динамики.

В зависимости от способов выражения уровней ряды динамики подразделяются на ряды абсолютных, относительных и средних вели­чин.

Ряды динамики абсолютных величин являются исходными, пер­вичными, так как лежащие в их основе абсолютные показатели полу­чаются непосредственно при подсчете итогов статистического наблю­дения.

Ряды динамики, выраженные относительными и средними вели чинами, являются вторичными, производными, рассчитанными на ос­нове рядов динамики абсолютных величин. Ряды относительных ве­личин могут характеризовать темпы роста определенного показателя изменение удельного веса показателя в совокупности (например удельного веса городского населения в его общей численности), изме­нение показателей интенсивности (например, ВВП на душу населе­ния, коэффициента рождаемости).

В зависимости от времени,отраженному в рядах динамики, раз­личают интервальные и моментные ряды.

Интервальный (периодический) ряд динамики — это ряд, уровни которого характеризуют размеры общественно-экономических явле­ний за определенные периоды времени.

Уровни интервального ряда динамики, как правило, являются объемными показателями, которые зависят от интервала времени.

Ряды динамики с нарастающими итогами строятся, например, при определении общего объема товарооборота в розничной торговле пу­тем обобщения товарно-денежных отчетов за последние операцион­ные периоды (пятидневки, недели, декады и т.д.).

Моментный ряд динамики — это ряд, уровни которого характе­ризуют величину социально-экономического явления по состоянию на определенные моменты времени, определенные даты.

Уровни моментного ряда динамики не связаны с интервалом вре­мени, а выступают как показатели наличия или численности на мо­мент времени.

Ряды динамики с нарастающими итогами строятся, например, при определении общего объема товарооборота в розничной торговле пу­тем обобщения товарно-денежных отчетов за последние операцион­ные периоды (пятидневки, недели, декады и т.д.).

Моментный ряд динамики — это ряд, уровни которого характе­ризуют величину социально-экономического явления по состоянию на определенные моменты времени, определенные даты.

Уровни моментного ряда динамики не связаны с интервалом вре­мени, а выступают как показатели наличия или численности на мо­мент времени.

По полноте времени, отраженного в рядах динамики, их подразделяют на ряды полные и неполные.

В полных рядах даты или периоды следуют друг за другом с равным интервалом. В неполных рядах — в последовательности времени равный интервал не соблюдается.

По содержанию показателейразличают ряды частных и агре­гированных показателей. Частные показатели характеризуют явление односторонне, изолированно. Например, объем произведенной продук­ции на предприятии за день. Агрегированные основаны на частных по­казателях и характеризуют изучаемый процесс комплексно. Напри­мер, чтобы иметь представление об экономике в целом, рассчитывают агрегированный показатель ВВП.

По числу показателейвыделяют изолированные и комплексные (многомерные) ряды динамики. Если ведется анализ во времени од­ного показателя, то ряд динамики будет называться изолированным.

Комплексный ряд динамики получается в том случае, когда в хро­нологическом порядке дается система показателей, связанных между собой единством процесса или явления.

В зависимости от наличия основной тенденцииизучаемого процесса ряды динамики делятся на стационарные и нестационарные. Если основные характеристики случайного процесса (математическое ожидание значения признака, дисперсия) постоянны, не зависят от времени, то процесс считается стационарным. В противном случае - нестационарным.

При построении динамических рядов следует соблюдать следующие правила их пост­роения.

1. Периодизация развития — разделение ряда по времени на од­нородные этапы, в пределах которых показатель подчиняется одному закону развития. По существу это типологическая группировка во вре­мени.

2. Величины временных интервалов должны соответствовать интенсивностиизучаемых процессов. Чем больше вариация уровней во времени, тем чаще должны быть сделаны замеры значений показа­телей. Соответственно для стабильных процессов интервалы можно увеличить.

3. Численные уровни рядов динамики должны быть упорядочены во времени.Не допускается анализ рядов динамики с пропусками от­дельных уровней, если это неизбежно, то уровни восполняют расчет­ными значениями.

4. Статистические данные рядов динамики должны быть достоверны.

5. Важнейшее требование построения динамических рядов заключается в том, что статистические данные должны быть сопоставимы.

В силу того, что ряды динамики характеризуют явления за длительный промежуток времени, в течение которого могли произойти изменения, необходимо следить за тем, чтобы все уровни ряда были сопоставимы между собой: по территории, полноте охвата, экономи­ческому содержанию, моменту регистрации; исчислены по одной ме­тодике, в одних и тех же единицах измерения и ценах.

Несопоставимость территории возникает вследствие изменений границ стран, областей, районов (присоединение или отделение отдель­ных частей территорий). Для приведения данных к сопоставимому виду производится пересчет прежних данных с учетом новых границ.

Несопоставимость по полноте охвата различных частей явления возникает, например, в результате перехода ряда объектов из одного подчинения в другое. Сопоставимость по кругу объектов не наруша­ется, если появились предприятия, построенные заново, или выбыв­шие предприятия прекратили свою работу. Сопоставимость по кругу объектов достигается смыканием динамических рядов, при котором абсолютные уровни заменяются относительными.

Несопоставимость по экономическому содержанию возникает в том случае, когда изменяется «понимание» единиц наблюдения. На­пример, при изучении «малых предприятий» сначала необходимо оп­ределить, какие предприятия являются малыми.

Несопоставимость по критическому моменту времени возникает, как правило, в моментных рядах динамики с сезонным характером уровней. Например, в течение ряда лет учет скота проводился по со­стоянию на 1 октября, а затем — на 1 января. Ряд динамики нельзя считать сопоставимым, если в нем уровни относятся к разным датам регистрации.

Несопоставимость по методике расчета возникает в случае, если существует разная методика расчета отдельных показателей или она изменяется во времени. Например, в одни годы урожайность считали с засеянной площади, а в другие — с убранной; производительность труда может быть рассчитана на одного рабочего и на одного работни­ка предприятия.

Особенно остро стоит эта проблема при международных сопоставлениях.

Несопоставимость из-за различия единиц измерения может при вести к разному характеру динамики одного и того же явления.Например, разная динамика отмечается при построении динамических рядов в строительстве квартир, если они представлены по количеству, квадратных метрах площади и стоимости. Однако если в этом случае построить параллельно три ряда динамики, то они будут аналитиче­ски дополнять друг друга.

При анализе показателей в стоимостном выражении следует учи­тывать, что с течением времени происходит непрерывное изменение цен, что приводит к несопоставимости рядов динамики по ценам. При­чин для этого множество: инфляция, рост затрат, рыночные условия (спрос и предложение) и др.

Чтобы привести ряды динамики к сопоставимому виду, необхо­димо при характеристике стоимостных показателей объема продукции во времени устранить влияние изменения цен. Это достигается путем переоценки произведенной продукции в цены одного периода, кото­рые называют фиксированными или сопоставимыми ценами.

Для приведения ря­дов динамики к сопоставимому виду существуют различные приемы и методы: прямого пересчета, смыкания рядов динамики, приведения к одному основанию. Рассмотрим каждый из методов.

Наиболее простым методом является метод прямого пересчета. Если динамические ряды несопоставимы в силу изменения круга объектов учета или территориальных границ или изменения методи­ки расчета, то для обеспечения сопоставимости проводится прямой пересчет данных по первичному материалу.

Если в распоряжении экономиста нет сведений, необходимых для прямого пересчета за все годы, а есть лишь уровень за один и тот же год, исчисленный в старых и новых границах или по прежней и по но­вой методологии, то единый динамический ряд может быть получен с помощью особого приема, называемого смыканием рядов динамики.

Под смыканием рядов динамики понимается объединение в один (более длинный) двух или нескольких рядов, уровни которых исчислены по разным методикам, в разных границах. Смыкание рядов динамики дает возможность устранить обрывочность сведений и полу­чить единый ряд за весь промежуток времени.

Сопоставления во времени показателей отдельных стран, областей, районов и т.д. называются сравнительным анализом динамик» В параллельных сравнениях показателей также возникают проблем сопоставимости уровней, но уже нескольких сравнимых между собой рядов. Для этого используют метод приведения к одному основанию т.е. к одному и тому же моменту или периоду времени, уровень кото­рого принимается за базу сравнения.

Сущность данного метода заключается в том, что данные о вели­чине исследуемого показателя за год, принятый за базу сравнения принимают равным 100%, а уровни остальных лет относят к нему, вы­ражая частное в процентах. В относительных величинах происходит нивелирование несопоставимости уровней динамических рядов, и ха­рактер развития становится более наглядным.

Для сравнения роста показателей используют коэффициент опе­режения, который рассчитывается как отношение темпов роста или темпов прироста за сравниваемые отрезки времени.

Коэффициент опережения, рассчитанный через темпы роста, яв­ляется величиной положительной, так как темпы роста не могут быть отрицательными.

Рассчитать коэффициент опережения через темпы прироста не всегда возможно, так как темп прироста может иметь и положитель­ный, и отрицательный знаки. Находить отношение величин с разны­ми знаками бессмысленно, так как отрицательный коэффициент опе­режения лишен логического смысла.

Параллельные сравнения становятся более наглядными, если рас­сматривать среднегодовые темпы прироста показателей.

Расчет большей части показателей основан на сравнении между собой уровней ряда динамики. Сравниваемый уровень называют те­кущим, а уровень, с которым производится сравнение, — базисным. За базисный уровень принимают либо предыдущий уровень, либо началь­ный в исследуемом ряду распределения.

В случае, когда сравнение производится с одним и тем же перио­дом (моментом) времени, начальным в ряду динамики и выступаю­щим в качестве постоянной базы сравнения, получают базисные пока­затели. Если сравнение производится с предыдущим периодом (моментом) времени, то получают цепные показатели, так как они представляют собой как бы отдельные звенья цепи.

Средний уровень интервального ряда определяют по формуле

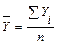
где n - число членов ряда динамики.

Средний уровень моментного ряда определяют по формуле средней хронологической:

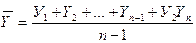
Абсолютный прирост DУi показывает на сколько единиц увеличился (или уменьшился) анализируемый уровень ряда Уi относительно базисного уровня У0 (по базисной схеме) или уровня предшествующего года Уi-1 (по цепной схеме). Соответственно его определяют по формулам:

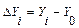(по базисной схеме)

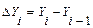(по цепной схеме)

Темп роста Тр показывает во сколько раз анализируемый уровень ряда увеличился (или уменьшился) по сравнению с уровнем принятым за базу сравнения (по базисной схеме) или предшествующим уровнем (по цепной схеме). Темп роста выражают в процентах или отвлеченных числах (коэффициент роста). Его определяют по формулам:

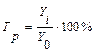(по базисной схеме)

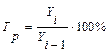(по цепной схеме)

Темп прироста Тпр показывает, на сколько процентов увеличился (или уменьшился) анализируемый уровень ряда по сравнению с базисным (по базисным схеме), или предшествующим уровнем ряд (по цепной схеме). Его определяют как отношение абсолютного прироста к уровню, принятому за базу сравнения по формулам:

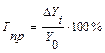(по базисной схеме)

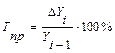(по цепной схеме)

Темпы роста и прироста связаны между собой, что видно из формул их расчета

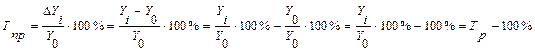
Это дает основание определить темп прироста через темп роста.

Тпр=Тр-100%

Средний темп роста и средний темп прироста характеризуют соответственно темпы роста и прироста за период в целом. Средний темп роста рассчитывается по данным ряда динамики по формуле средней геометрической:

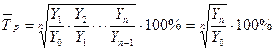
где n - количество цепных коэффициентов роста.

Исходя из соотношения темпов роста и прироста определяется средний темп прироста:

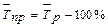
Абсолютное значение одного процента прироста А - это отношение цепного абсолютного прироста к цепному темпу прироста выраженному в процентах. Оно определяется по формуле:

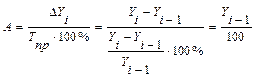
Как видно из расчета абсолютное значение одного процента прироста равно 0,01 предшествующего уровня.

С помощью рядов динамики изучают явления, имеющие сезонный характер. Сезонными колебаниями называются устойчивые внутригодовые колебания в ряду динамики, обусловленные специфическими условиями производства, потребления или продажи продукции или услуг. Например, потребление топлива или электроэнергии для бытовых нужд, перевозки пассажиров, продажи товаров.

Уровень сезонности оценивается с помощью индексов сезонности. Индекс сезонности показывает, во сколько раз фактический уровень ряда в момент или интервал времени больше среднего уровня. Он определяется по формуле:

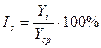
Где: Is- уровень сезонности:

Уi - текущий уровень ряда динамики;

Уср – средний уровень ряда.

Графически индекс сезонности может быть представлен с помощью полигона – основного вида графиков, используемого для графического изображения рядов динамики.

ИНДЕКСНЫЙ МЕТОД

Для характеристики изменений одноименных явлений исполь­зуют относительные показатели динамики, сравнения, выполнения плана и т.д. Однако в статистике часто приходится сопоставлять не только отдельные элементы совокупности, но и многие сложные явле­ния, состоящие из разнообразных, не поддающихся суммированию элементов. Например, продукция промышленности состоит из сово­купности разнообразных явлений (ткань, продукты питания, мебель и т.д.). Встает задача соизмерения этих разнообразных явлений, кото­рая в статистике решается с помощью индексного метода.

С помощью индексов могут решаться следующие задачи:

1) определение изменения сложных, непосредственно несоизмери­мых совокупностей во времени (индексы как показатели динамики);

2) оценка степени выполнения плана по совокупности в целом и ее частям (индексы выполнения плана);

3) установление соотношения сложных явлений в пространстве (территориальные индексы);

4) измерение влияния структуры совокупности на динамику сред­него уровня явления (индексы структурных сдвигов);

5) приведение несоизмеримых явлений к соизмеримому виду (ин­дексы выступают как синтетическое средство);

6) определение степени влияния отдельных факторов в общем изменении сложных явлений (индексы выступают как аналитическое средство).

Среди перечисленных задач в современном анализе доминиру­ющей является последняя. Давая статистическую оценку влияния от­дельных факторов на динамику результативного признака, индексы выступают важным измерителем связи признаков, имея тем самым научное и практическое значение.

Индексный метод — это один из способов перехода от абстракт­ного выражения качеств явления к набору конкретных показателей.

Индекс является относительной величиной, но не все относитель­ные величины являются индексами. Индекс в отличие от относительной величины, которая характеризует изменение какого-либо единич­ного явления или такого массового явления, отдельные элементы которого можно суммировать, характеризует относительное изменение сложного явления, состоящего из качественно однородных, но не под­дающихся суммированию элементов.

Отдельные виды относительных величин могут характеризовать соотношения как одноименных, так и разноименных явлений, а ин­декс характеризует соотношение только одноименных явлений, напри­мер производительности труда, цен, себестоимости и др.

Таким образом, индекс — это особый относительный показатель, характеризующий соотношения массовых общественных явлений, со­стоящих из качественно однородных, но непосредственно не подда­ющихся суммированию элементов, во времени, в пространстве или в сравнении с любым эталоном (планом, нормативом, прогнозом, по­казателями лучших предприятий).

При расчете индекса необходимо сопоставление не менее двух величин. Необходимо различать величину сравнения (числитель индек­сного соотношения) и базу сравнения (знаменатель индексного соот­ношения). Основным элементом индексного отношения является ин­дексируемая величина, изменение которой характеризует индекс. Индексирование — это процедура выражения главного содержания яв­ления с помощью количественных величин.

Базисный период — это период, к которому относится величина, принимаемая за базу сравнения, период, с которым производится срав­нение. Отчетный (текущий) период — это период, к которому отно­сится величина, подвергающаяся сравнению, период, который срав­нивается с базисным.

Индексы группируются по различным направлениям: по охвату элементов; по базе сравнения; по виду весов; по форме построения; по составу явления; по содержанию индексируемых величин; по объек­ту исследования.

Экономические явления, развитие которых должны характеризо­вать индексы, являются, как правило, сложными, состоящими из мно­гих элементов. Индексы рассчитываются как для отдельных элементов сложного явления, так и для всего явления в целом. По охвату элемен­тов индексы делятся на индивидуальные, групповые и общие.

Рассмотрим методику их построения.

Индивидуальные индексы являются относительными величинами, характеризующими изменение только одного элемента сложного яв­ления. Обязательным условием для расчета индивидуального индек­са является максимальная однородность того объекта, для которого он вычисляется.

Индивидуальный индекс характеризует изменения явления, состоящего из однородных элементов, и предоставляет собой обычную относительную величину динамики, выполнения плана, сравнения. Индивидуальный индекс обозначают буквой i с подстрочным указанием индексируемого показателя. Индексируемым называют показатель, изменение которого характеризует индекс. Так, например, для характеристики выполнения планового задания по производству отдельных видов продукции рассчитывают индивидуальные индексы физического объема продукции по формуле.

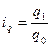
где 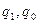- объем производства какого-то вида продукции в натуральном выражении соответственно в отчетном и базисном периодах, который является индексируемой величиной.

Групповые индексы или субиндексы используются при изучении сложных явлений, подвергнутых группировке. Они характеризуют изменение не всего сложного явления, а определенной его части. На­пример, динамику цен по отдельным видам или группам продоволь­ственных товаров.

Общие индексы характеризуют соотношение сложного экономи­ческого явления в целом, состоящего из нескольких качественно од­нородных элементов, которые нельзя непосредственно суммировать. Так, каждое промышленное предприятие, как правило, выпускает раз­личные виды продукции. Невозможность непосредственного сумми­рования видов продукции объясняется не только различием натураль­ных единиц измерения, но и различием потребительных свойств, неодинаковой натурально-вещественной формой продукции.

Индексы, используемые для характеристики динамики объемов со­вокупностей, например объема произведенной продукции, объема про­данных товаров, называются индексами объемных показателей. С помо­щью индексов характеризуют динамику показателей, являющихся сред­ними или относительными величинами: цену или себестоимость едини­цы продукции, производительности труда и т. д. Эти индексы называют ин­дексами качественных показателей.

Чтобы охарактеризовать в виде сводного показателя изменение сово­купностей, состоящих из непосредственно несопоставимых элементов, необходимо эти элементы привести к тому единству, которое делает их соизмеримыми, т. е. найти для них общую меру. Например, для продук­ции как совокупности различных изделий, работ и услуг характерным явля­ется то, что она представляет результат производства, предназначенный для продажи. Следовательно, продукция—потребительная стоимость для ее покупателей, и в процессе ее продажи происходит общественное признание затраченного при ее производстве труда. Затраты труда могут быть выраже­ны непосредственно в единицах времени (например, в часах) и в стоимост­ной форме (например, в рублях). Общепринятой формой выражения обще­ственно необходимых затрат труда является стоимостная форма, именуе­мая ценой единицы продукции.

В результате приведения различных видов продукции к соизмеримо­му виду путем умножения ее количества на цену продажи получаются абсолютные суммарные показатели стоимости продукции, которые за­висят от обоих сомножителей. Изменение любого из них приводит к из­менению стоимости продукции.

Поэтому результат сопоставления абсолютных суммарных показате­лей, полученных вследствие приведения различных единиц совокупнос­ти к соизмеримому виду, будет характеризовать совместное изменение нескольких показателей. Например, сопоставление стоимости продукции произведенной в двух периодах, характеризует одновременно измене­ние количества продукции и цен. Поэтому в тех случаях, когда необходимо измерить изменение одного показателя, необходимо отвлечься от динами­ки остальных показателей, оказывающих влияние на общий результат.

Сводный индекс характеризует изменения явления, состоящего из разнородных непосредственно не суммируемых элементов.

Чтобы охарактеризовать при помощи индексов изменение явлений, состоящих из разнородных элементов, необходимо прежде всего обеспечить возможность суммирования этих элементов для их дальнейшего сопоставления. Для этого следует привести их в соизмеримый вид посредством специального соизмерителя который, являясь общей мерой этих явлений, выражает то общее, что им присуще, Так, для продукции народного хозяйства как совокупности разноименных видов изделий, несмотря на их различные потребительские свойства, общим является то, что все они представляют собой результат труда, затраты которого могут быть выражены как в единицах рабочего времени, например человеко-часах, так и в стоимостной форме, имеющей денежное выражение. Эти показатели: время, стоимость - могут быть использованы как соизмерители и называются весами индекса. Умножив индексируемый показатель на соответствующий вес, мы тем самым выражаем элементы анализируемой совокупности в одних единицах измерения, т.е. проводим их в соизмеримый вид, поэтому их уже можно суммировать и сопоставлять. Так, например, умножив объем различных видов изделий на их себестоимость, мы выражаем их в стоимостной форме, что позволяет их суммировать и сопоставлять. При этом, чтобы индекс отражал изменение только индексируемой величины, веса индексов берут на одном уровне. Если в качестве веса используются объемные показатели (продукция, численность), их берут на уровне текущего периода, если качественные показатели (план, себестоимость, затраты времени на единицу продукции), то их принимают на уровне базисного периода.

В народном хозяйстве широко используются индексы физического объема продукции, индекс себестоимости, индекс затрат, индекс реализованной продукции, индекс цен, индекс товарооборота, индекс производительности труда, индекс удельного расхода материалов и др.

Сводный индекс физического объема продукции Iq в общем виде определяется по формуле

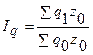
где q1, q0 - объем продукции каждого вида изделий соответствующего периода (индексируемый показатель);

z0 - себестоимость каждого вида изделий базисного периода (вес индекса).

Сводный индекс себестоимости 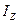определяют по формуле

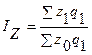
где z1, z0 - себестоимость отдельных видов продукции соответственно в текущем и базисном периодах.

Он характеризует, как в среднем изменяется себестоимость продукции различных видов в целом по анализируемой совокупности.

Сводный индекс затрат Izq определяют по формуле

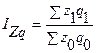
где z1q1, z0q0 - затраты по производству различных видов продукции соответственно в отчетном и базисном периодах.

Он характеризует, как изменились затраты по производству продукции различных видов в целом по анализируемой совокупности.

Сводный индекс цен Ip определяют по формуле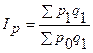

где р1 , р0 - цена отдельных видов продукции соответственно в текущем и базисном периодах.

Он характеризует, как изменились в среднем цены на различные виды продукции по анализируемой совокупности.

Статистические органы определяют различные индексы цен: розничной, оптовой, рыночной торговли и др. Особое значение приобретает расчет индексов розничных цен в условиях инфляции, когда возникает необходимость в ин­дексации денежных доходов различных категорий населения. Для получения точных данных о значениях индексов розничных цен необходимо иметь сведе­ния о цене каждого отдельного товара и количестве реализованных по ней единиц в натуральном выражении. При наличии в России различных видов торговли (государственной, частной, рыночной, с руки, др.), хаотическом росте цен и разнице цен на одинаковую продукцию по стране получить необходимые данные практически невозможно.

В подобных условиях статистические органы обычно прибегают к выборочной регистрации на определенные даты цен определенных групп товаров и использованию стандартной структуры их покупок. Выбороч­ные данные семейных бюджетов о наборе приобретаемых товаров назы­вают потребительской корзиной. Полученные на основе подобной ин­формации индексы цен являются, как правило, приблизительными, они нуждаются в квалифицированной экспертной оценке, а поэтому обычно называются оценочными.

При экспертной оценке индексов цен потребительских товаров необ­ходимо учитывать тот факт, что они в значительной мере зависят от со­поставимого ассортимента, т. е. той их совокупности, стоимость кото­рой может быть определена в ценах сопоставляемого периода и перио­да, принятого за базу сравнения.

При значительном росте цен в течение длительного периода исполь­зование сопоставимого ассортимента текущего и базисного периодов неизбежно приводит к некоторому занижению индекса цен, поскольку с повышением цен уменьшается потребление дорогостоящих товаров. Поэтому в таких условиях целесообразно в качестве сопоставимого ас­сортимента потребительских товаров (стандарта) использовать тот их набор, который покупался населением в течение ряда лет при более или менее стабильных ценах. В условиях, когда рост цен на товары рознич­ной торговли происходит без улучшения их качества, индекс цен может быть принят в качестве индекса инфляции.

Сводный индекс товарооборота Iqp определяют по формуле

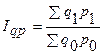
где q1p1, q0p0 - размер товарооборота соответственно в текущем и базисном периодах.

Сводный индекс производительности труда I1/t определяют по формуле

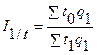
где t1, t0 - затраты времени на производство единицы продукции соответственно в текущем и базисном периодах.

Он характеризует изменение производительности труда, является показателем, обратным индексу трудоемкости It, который определяю по формулам:

;

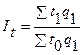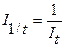
Он характеризует, как в среднем изменились затраты времени на единицу продукции в связи с ростом производительности труда.

Сводный индекс массы отработанного времени Iqt определяют по формуле:

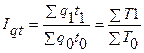
где q1t1(T1), q0t0(T0) - это время, затраченное на производство всей продукции соответственно в текущем и базисном периодах.

При условии создания одним работником (звеном или бригадой) несколь­ких видов продуктов труда возникает необходимость расчета общих индек­сов производительности труда (выработки). Она решается путем соизмере­ния продуктов труда с помощью норм труда и стоимостного показателя зат­рат живого труда на создание единицы продукта труда. Исходя из этого, воз­можен расчет общих индексов производительности труда (выработки) по трудовому и стоимостному методам.

Сводный индекс удельного расхода материалов Im , топлива определяют по формуле

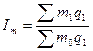
где m1, m0 - удельный расход материалов (топлива), т.е. расход материалов (топлива) на единицу продукции соответственно в текущем и базисном периодах.

Он характеризует, как изменился в среднем расход различных видов материалов, топлива на единицу продукции.

Расчет индексов может быть выполнен в агрегатной форме и форме средних индексов - среднеарифметического взвешенного и среднегармонического. Все вышеприведенные индексы рассчитаны как агрегатные индексы. Выбор формы расчета индексов зависит от наличия исходных данных. Если известны значения индексируемого показателя и веса в текущем и базисном периодах, то пользуются агрегатной формой индексов. Если отсутствуют значения индексируемого показателя или веса в текущем или базисном периодах, но известны изменения индексируемого показателя или веса по отдельным единицам анализируемой совокупности, пользуются формой средних индексов. Например, известны плановый размер затрат по выпуску продукции на предприятии q0z0 и задание по росту выпуска продукции отдельных видов iq. Необходимо определить индекс физического объема продукции Iq. Индекс физического объема продукции определят по формуле

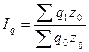
Для решения задачи неизвестен фактический выпуск продукции, но задан рост каждого вида продукции 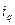, который определяют по формуле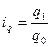

Отсюда определяем q1:

q1=i_qq₀

Подставляем найденную величину в исходную формулу

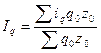
Это есть не что иное, как средняя арифметическая взвешенная индекса физического объема. Соответственно индекс называют среднеарифметическим индексом. Или, например, известны размер товарооборота в отчетном q₁p₁ и плановом периодах q₀p₀, а также изменения цен в отчетном периоде относительно планового по отдельным видам изделий i_p. Необходимо определить, как в среднем изменились цены по всем видам изделий, т.е. индекс цен .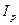

Индекс цен определяют по формуле

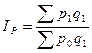
В нашем примере известен товарооборот в отчетном периоде p₁q₁ , а товарооборота в ценах планового периода нет, но заданы индивидуальные индексы цен по каждому виду изделий 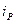, которые определяют по формуле

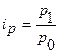
Отсюда можно определить цены планового периода

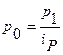
Подставляем их в исходную формулу

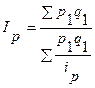
Это есть не что иное, как средняя гармоническая индекса цен. Соответственно его называют среднегармоническим индексом.

Индексы подчиняются той же взаимосвязи, что и характеризуемые ими показатели. Так, например, затраты определяют как произведение себестоимости продукции на объем продукции, соответственно и индекс затрат равен произведению индекса себестоимости и индекса физического объема продукции Iqz=IzIq

Докажем это:

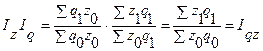
Пользуясь взаимосвязью индексов, можно по величине двух из них определить величину третьего. Например, известно, что по плану на предприятии ожидается рост выпуска физического объема продукции на 18% и снижение себестоимости изделий в среднем на 3%. Необходимо определить изменение затрат на заданный объем работ. Пользуясь взаимосвязью индексов затрат Iqz физического объема Iq и себестоимости Iz определяем изменение затрат

Iqz = Iq Iz= 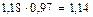или 114%

Таким образом, индекс затрат составляет 114%, т.е. затраты вырастут на 14%.

Индексы широко используются в факторном анализе для выявления меры влияния факторных показателей на средний уровень определяемого или результативного показателя.

Таким образом, существует общее правило построения системы взаи­мосвязанных индексов: необходимо в паре взаимосвязанных индексов факторных показателей фиксировать веса на уровнях разных периодов. Если это правило нарушается, например ве