Вход потока в трубу
Экспериментальными исследованиями установлено, что сопротивления зависят от толщины  передней кромки круглой трубы. Для кромки с относительной толщиной
передней кромки круглой трубы. Для кромки с относительной толщиной 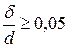 коэффициент местных сопротивлений на входе
коэффициент местных сопротивлений на входе 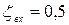 . При бесконечно малой толщине кромки (
. При бесконечно малой толщине кромки (  )
) 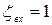 .
.
Для уменьшения сопротивления на входе применяются входные наконечники конической формы или с плавным входом (рис. 4.20). В случае наличия перед входом в трубу экрана потери увеличиваются. В таких наконечниках весьма существенно уменьшается отрыв потока от стенок. Для конусных наконечников с 
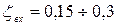 , наконечников с плавным входом -
, наконечников с плавным входом - 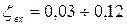 при
при 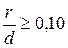 .
.
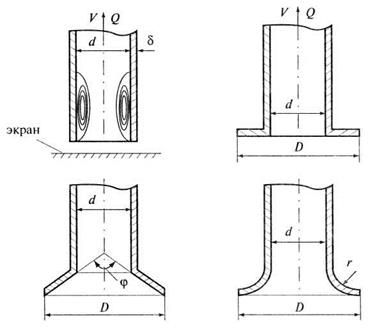
Рис. 4.20. Различные входы в трубу
 Диафрагма на трубопроводе
Диафрагма на трубопроводе
Диафрагма устанавливается на трубопроводе для регулирования расхода воды в определенном месте. Трубопровод в месте установки диафрагмы имеет постоянное живое сечение, d=const (рис. 4.21).
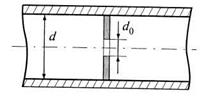
Рис. 4.21. Диафрагма на трубопроводе
Коэффициент местного сопротивления диафрагмы определяется по формуле
 , (4.145)
, (4.145)
где 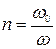 - отношение площади отверстия диафрагмы диаметром
- отношение площади отверстия диафрагмы диаметром 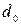 к поперечной площади сечения трубы диаметром
к поперечной площади сечения трубы диаметром 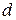 ;
; 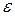 - коэффициент сжатия при прохождении потока через отверстие диафрагмы,
- коэффициент сжатия при прохождении потока через отверстие диафрагмы, 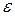 рекомендуется находить по формуле А. Альтшуля (4.143):
рекомендуется находить по формуле А. Альтшуля (4.143):
 .
.
Закругление трубы
Плавно закругленные трубы или поворот трубы называют отводом. Радиус кривизны R влияет на вихреобразование потока жидкости, т.е. на сопротивление движению (рис. 4.22). Известна формула Вейсбаха по определению коэффициента местных сопротивлений при соблюдении следующих условий: 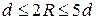 :
:
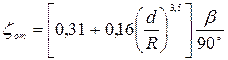 , (4.146)
, (4.146)
где  - угол закругления.
- угол закругления.

Рис. 4.22. Закругления труб: а - плавное закругление (отвод); б - резкое закругление
В случае резкого поворота трубы (рис. 4.22, б) возникают существенно большие потери напора. В результате действия центробежных сил происходит отрыв от стенок потока жидкости с вихреобразованием, приводящий к возникновению водоворотной области.
Для такого круглого колена коэффициент 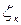 зависит от угла наклона осей колена
зависит от угла наклона осей колена  . При
. При 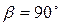
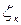 находится в пределах значения 1,0. В случае большой шероховатости стенок
находится в пределах значения 1,0. В случае большой шероховатости стенок 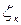 будет больше единицы.
будет больше единицы.
Дата добавления: 2016-02-27; просмотров: 982;
