Примеры решения задач. Пример 3.2.3. Температура поверхностей стены компрессорного цеха высотой 4 м равна tс=10 0С температура воздуха в цехе составляет tв=25 0С
Пример 3.2.3. Температура поверхностей стены компрессорного цеха высотой 4 м равна tс=10 0С температура воздуха в цехе составляет tв=25 0С. Определить коэффициент теплоотдачи от воздуха к стене цеха.
Решение
Теплообмен здесь осуществляется за счет свободной конвекции, следовательно, необходимо воспользоваться уравнением 3.2.11. Критерии 
и Pr определяется уравнениями 3.2.13 и 3.2.15.
.
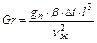В данном случае определяющим размером у критерия Gr будет высота цеха l=4 м,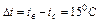 
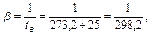К-1.
Кинематическая вязкость воздуха при температуре tв=25 оС составит ν=15,53∙10-6 м2/с. Следовательно,
Физические параметры воздуха при температуре tв=25 оС, составляют: плотность ρ=1,185 кг/м3; теплоёмкость Ср=1,005 кДж/кг∙К=1005 Дж/кг∙К; кинематическая вязкость ν=15,53∙10-6 м2/с; коэффициент теплопроводности λ=2,634∙10-2 вт/м∙К.
Следовательно, критерий Прандтля равен:
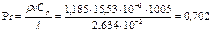
Произведение критериев Gr и Pr составляет
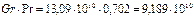
Согласно данным табл. 3.2.1 режим движения воздуха здесь будет турбулентным, следовательно, коэффициенты уравнения 3.2.11 будут в данном случае равны С=0,15, т=0,33.
Критерий Нуссельта:
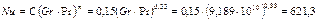
Отсюда по уравнению 3.2.12 коэффициент теплоотдачи
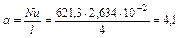Вт/м2∙К.
По уравнению 3.2.10 плотность теплового потока равна
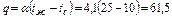Вт/м2.
Пример 3.2.4. Определить коэффициент теплоотдачи от газа к внутренней поверхности газопровода диаметром d=1020 мм, если температура стенки трубы tc=40 0С, а температура газа в трубе tг=60 0С. Линейная скорость газа w=3 м/с. Газ - метан. Давление в трубопроводе 4 МПа.
Решение
При теплообмене в трубах определяющим критерием, характеризующим режим течения, является критерий Рейнольдса
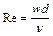
Коэффициент кинематической вязкости входящий в критерий Рейеольдса связан с коэффициентом динамической вязкости уравнением
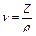, м2/с,
где ρ - плотность газа. Считая газ в первом приближении идеальным, подчиняющимся уравнению Клайперона (РV=RT) плотность метана (СН4) равна:
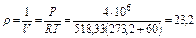кг/м3,
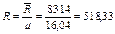Дж/кг∙К.
Коэффициент динамической вязкости при параметрах Р=4 МПа и t=60 0С составляет Z=12,57∙10-6 Н∙с/м2=12,57∙10-6 кг/м∙с.
Следовательно, кинематическая вязкость
м2/сек.
Следовательно, критерий Рейнольдса в данном случае будет равен
.
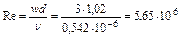Так как режим движения явно турбулентный, то расчет теплообмена производится по формуле:
.
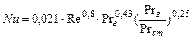При температурах газа tг=60 0С и стенки трубы tс=40 0С численные значения физических величин ν, ρ, Ср, λ, входящих в критерий Прандтля, равны при температуре tг=60 0С:
ν=0,542∙10-6 м2/с; ρ=23,2 кг/м3; Ср=2,507 кДж/кг∙К; l=86,7∙10-3Вт/м∙К.
При температуре tc=40 0C:
ν=0,487∙10-6 м2/с; ρ=24,64 кг/м3; Ср=2,507 кДж/кг∙К; l=86,7∙10-3 Вт/м∙К.
Следовательно, при температуре газа tг=60 0С, критерий Прандтля равен:
.
При температуре tс=40 0C, критерий Прандтля равен:
.
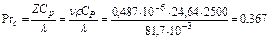Численные значения критерия Прандтля совпадают, следовательно, определение критерия Nu можно вести по уравнению:
,
Так как 
то при l=86,7∙10-3 Вт/м∙К.
кВт/м2∙К.
Следовательно, за единицу длины l=1 м от газа к стенке передается следующее количество тепла:
Ql=a∙f(tг-tс)=138,72∙pd(tг-tс)= 288,04∙3,14∙1,02(60-40)=18450,9 кВт.
Дата добавления: 2016-02-27; просмотров: 2488;