НАПОРНЫЙ ГИДРОТРАНСПОРТ
Перемещение (транспортирование) различных твердых частиц потоком воды по трубам за счет перепада давления называется напорным гидротранспортом.
При турбулентном режиме движения потока гидросмеси в трубе твердые частицы в результате пульсации скоростей и давления участвуют в турбулентном перемешивании. Для поддержания твердых частиц во взвешенном состоянии и на преодоление сопротивления их движению затрачивается дополнительная механическая энергия по сравнению с обычным потоком жидкости.
Дополнительные потери удельной механической энергии ∆hw при движении гидросмеси обычно выражают в виде относительных удельных потерь (гидравлического уклона):
 , (10.12)
, (10.12)
где l— длина трубопровода, на котором дополнительные потери напора равны ∆hw.
Относительные удельные потери механической энергии при гидротранспорте можно выразить следующей функциональной зависимостью:
∆i = f (Vs, ρo, μo, ρт, ds, z, β, D, k, α, Co), (10.13)
где VS — средняя скорость гидросмеси; ρ0, μ0 — плотность и вязкость жидкости; ρт — плотность частичек транспортируемого материала; ds — диаметр частички; β, z — параметры, характеризующие форму частиц и гранулометрический состав транспортируемого материала; D — диаметр трубопровода; k — шероховатость трубопровода; α — угол наклона трубопровода; С0 — объемная концентрация гидросмеси.
Для определения гидравлических потерь при транспортировании гидросмеси получило распространение следующее выражение:
is = io + ∆i, (10.14)
где i0 — гидравлический уклон при движении воды в трубе.
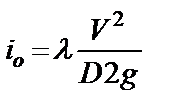 , (10.15)
, (10.15)
где λ — коэффициент гидравлического трения.
При гидротранспорте абразивных материалов, например песка, происходит уменьшение первоначальной шероховатости труб, т.е. имеет место шлифовка их внутренней поверхности. В связи с этим было установлено, что при расчете напорного гидротранспорта при определении коэффициента λ следует использовать формулы для гидравлически гладких труб.
Наиболее подходящей формулой, как было установлено экспериментами, для вычисления λ является формула П. Конакова для гидравлически гладких труб при Re > 105 (4.100).
Потери напора в трубопроводе при движении гидросмесиhk=isl
hls = isl. (10.16)
На рис. 10.3 представлены кривые изменения is от средней скорости в трубе V и плотности гидросмеси. Несущая жидкость — вода.
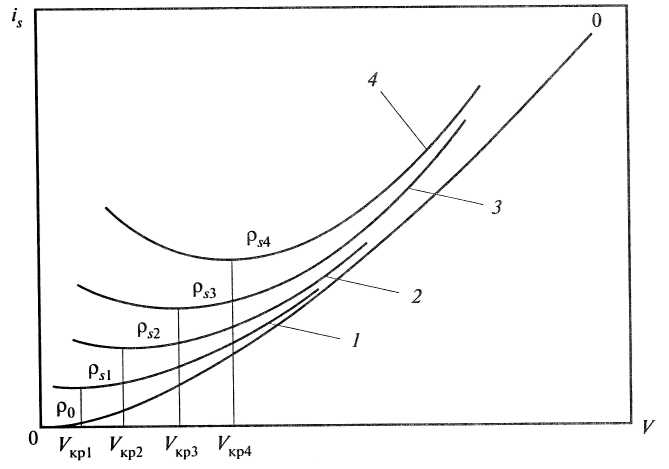
Рис. 10.3. Зависимость гидравлического уклона от плотности потока и скорости
Кривая 0 — изменение гидравлического уклона в зависимости от скорости движения воды в трубе, кривые 1, 2, 3, 4 — при движении потока гидросмеси соответственно плотностью ρs1, ρs2, ρs3, ρs4.
Плотности гидросмеси, показанные на рисунке, представлены в возрастающем порядке: ρs4 > ρs2 > ρs2 > ρs1 > ρ0.
Минимальные гидравлические потери (гидравлический уклон) имеют место при средних скоростях, равных критической скорости Vкр. При повышении плотности гидросмеси (концентрации) увеличиваются гидравлические потери и критическая скорость. Критическая скорость Vкр является одним из основных параметров при определении гидравлических потерь в трубопроводе и оптимального режима перемещения гидросмеси.
В связи с этим наиболее достоверные зависимости по определению hws и Vкр можно найти в результате экспериментальных исследований, в основу которых входят параметры, представленные выражением (10.13).
Получение теоретического решения для определения hws в связи со сложностью физического процесса перемещения частичек в потоке представляет собой весьма большие трудности. Имеющиеся теоретические формулы разных авторов не в полной степени соответствуют данным, полученным на основании экспериментальных исследований, выполненных на гидравлических стендах и в натурных условиях. Достаточно обширные экспериментальные исследования по гидротранспортированию однородных материалов были проведены Р. Дюраном в лаборатории в Гренобле. В качестве транспортируемых частиц использовался в основном однородный песок крупностью d = 0,2; 0,44 и 2,04 мм при диаметрах трубопровода D = 104; 150; 253; 380 и 406 мм. Трубы в опытах имели различную шероховатость k. Кроме песка в опытах применялись корундовый порошок, частички пластмассы и гравий крупностью до d=25 мм. Объемная концентрация гидросмеси изменялась до С0 = 23%. Относительная плотность гидросмеси в экспериментах была в пределах 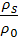 =1,5
=1,5 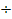 3,95.
3,95.
Используя теорию размерности и результаты опытов, Р. Дюран для определения ∆i предложил следующую зависимость:
 (10.17)
(10.17)
В зависимости (10.17) коэффициент лобового сопротивления Сφ характеризует размеры частиц (крупность) и форму частиц.
Критическая скорость по Дюрану
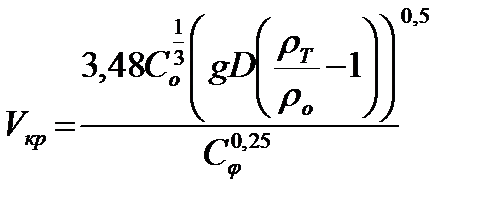 (10.18)
(10.18)
На основании исследований гидротранспорта разнородных песчаных и песчано-гравийных грунтов в трубах разных диаметров с различными концентрациями была предложена следующая формула для определения is:
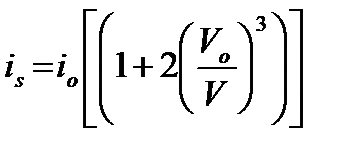 (10.19)
(10.19)
где V0 — средняя оптимальная скорость потока гидросмеси в трубе; V — фактическая средняя скорость гидросмеси в трубе.
Оптимальная скорость вычисляется по зависимости
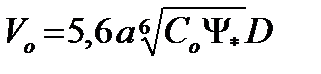 , (10.20)
, (10.20)
где a — поправочный коэффициент, зависящий от крупности частиц. В случае d 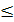 10 мм а=1. При d > 10 мм а = 1,05
10 мм а=1. При d > 10 мм а = 1,05 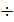 1,9; Ψ*, — коэффициент транспортабельности, параметр, определяющий фракционный состав материала (грунта).
1,9; Ψ*, — коэффициент транспортабельности, параметр, определяющий фракционный состав материала (грунта).
Для разнородного материала средневзвешенное значение коэффициента транспортабельности
 (10.21)
(10.21)
где Ψ*i — коэффициент транспортабельности для определенной фракции грунта (материала) di, Pi — процентное содержание фракции di
Значения Ψ*i определяются в зависимости от фракции грунта по табл. 10.1.
Таблица 10.1 Значение функции Ψ*i от материала
| Фракция грунта материала, | Ψ*i | Фракция грунта материала, мм | Ψ*i |
| 0,05-0,1 | 0,02 | 2-3 | 1,5 |
| 0,1-0,25 | 0,2 | 3-5 | 1,3 |
| 0,25-0,5 | 0,4 | 5-10 | 1,9 |
| 0,5-1 | 0,8 | 10 и более | |
| 1-2 | 1,2 |
Критическую скорость в трубе предлагается находить по формуле
 . (10.22)
. (10.22)
Расчет гидротранспорта сводится к определению критических скоростей и гидравлических потерь. Работа гидротранспортной установки должна осуществляться при скоростях, достаточно близких к критической скорости. Правильное вычисление Vкр , как уже отмечалось ранее, позволяет предотвратить осаждение сравнительно крупных частиц на дно трубы. Однако следует отметить, что при работе гидротранспортной установки расход гидросмеси и крупность материала изменяются со временем, в результате чего на дно трубопровода будет происходить осаждение твердых частичек. Слой осажденного материала — слой заиления, его называют телом заиления. Образовавшийся слой заиления высотой ∆hs уменьшает живое сечение трубопровода.
Для наклонных трубопроводов удельные гидравлические потери и критическая скорость вычисляются по следующим формулам:
isH = io + (is - io) cos α; (10.23)
Vкрн = Vкр cos α (10.24)
где α — угол наклона трубопровода, по которому перемещается гидросмесь.
При расчете гидравлических потерь в местных сопротивлениях учитывается плотность гидросмеси. Опытами установлено, что гидравлические потери в местном сопротивлении увеличиваются на величину 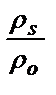 :
:
 . (10.25)
. (10.25)
где 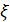 — коэффициент местных сопротивлений.
— коэффициент местных сопротивлений.
Значение i0 при разных скоростях и диаметрах приведены в табл. П1.7 приложения.
Пример 10.1
Гидросмесь плотностью ρs = 1150 кг/м3 транспортируется по стальному трубопроводу длиной l= 2000 м и диаметром D = 0,5м.
Плотность твердого материала ρт = 2,6 • 103 кг/м3. Средний размер частиц транспортируемого материала d = 0,35 мм. Определить расход гидросмеси Q и потери напора при условии, что гидротранспортирование должно производиться в пределах критической скорости.
Объемная концентрация гидросмеси по (10.5)
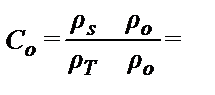
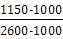 =0,0938
=0,0938
Критическая скорость по (10.22)
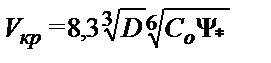
Коэффициент транспортабельности Ψ* находим при dср= 0,35 мм по табл. 10.1, Ψ*= 0,4
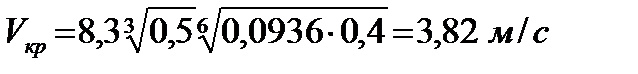 .
.
Расход гидросмеси
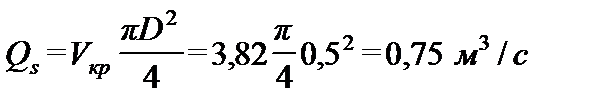 .
.
Оптимальная скорость по (10.20)
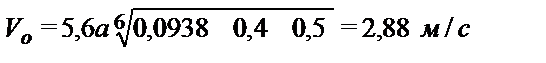 ,
,
а = 1, так как dcр < 10 мм,
is = i0 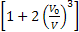
где i0 — гидравлический уклон при движении воды в трубе, вычисляется по формуле 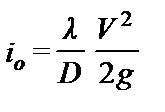 , а λ находим по формуле Конакова (4.100).
, а λ находим по формуле Конакова (4.100).
Число Рейнольдса
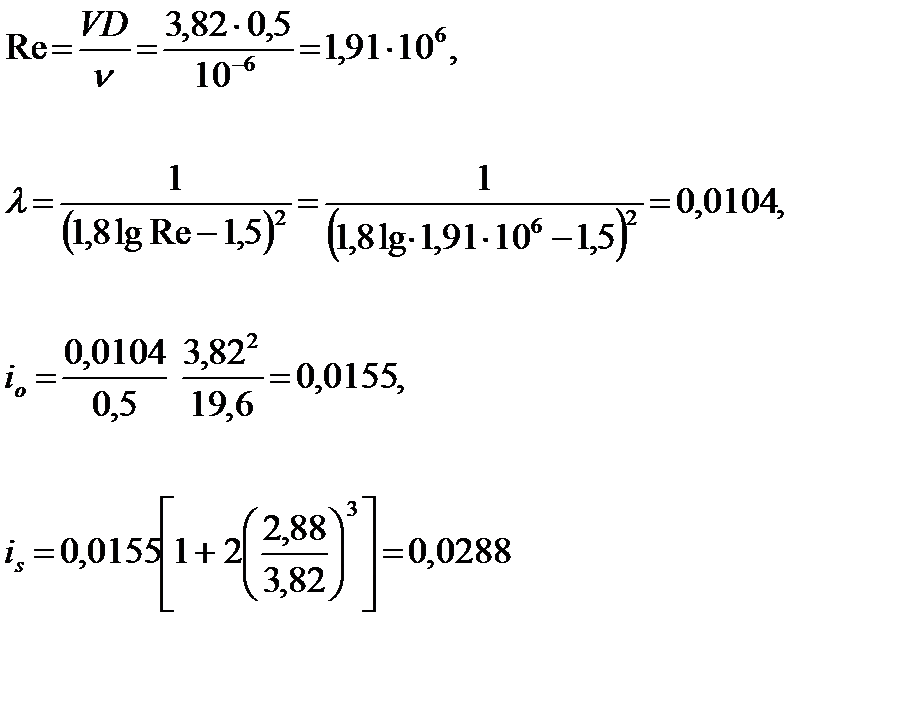 .
.
Гидравлические потери
hls = isl= 0,0288 · 2000 = 57.6 м.
Дата добавления: 2016-02-27; просмотров: 627;
