Основна термінологія та класифікація СПР

Сучасна теорія прийняття рішень розглядає узагальнену процедуру прийняття рішень як інформаційний синтез абстрактної системи, що забезпечує досягнення заданої цілі [12].

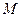Визначення 1.1.1. Абстрактною системою називається множина елементів, на якій реалізовано множину відношень (зв’язків) 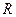, що впорядковують елементи в структуру

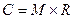.(1.1.1)

Структура (1.1.1) є нецілеспрямованою системою, оскільки вона не враховує множину властивостей 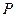, якими наділені елементи системи. Далі будемо розглядати тільки цілеспрямовані системи.

Визначення 1.1.2. Цілеспрямованою називається система 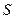, яка має впорядковану структуру:

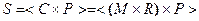. (1.1.2)

Визначення 1.1.3. СПР називається система, яка побудована на основі електронно-обчислювальної техніки і безпосередньо моделює когнітивні процеси, притаманні людині при прийнятті рішень.

СПР є обов’язковою важливою складовою частиною інтелектуальних систем різного призначення. У багатьох автоматизованих системах керування складними об’єктами та процесами СПР застосовується як система підтримки прийняття рішень (СППР). При цьому термін “підтримка” стосується таких систем, де вирішальне слово належить особі, що приймає рішення (ОПР).

Визначення 1.1.4. За існуючими стандартами[4] під функціонуванням СПР розуміється процес виконання системою заданого робочого алгоритму при використанні системи за призначенням, тобто за критерієм цілі створення системи.

Об`єднання широкого класу інтелектуальних систем поняттям СПР, не враховуючи їх відмінність за призначенням, обсягом інформаційних та керуючих функцій і складом комплекса технічних засобів (КТЗ), дозволяє з єдиних методологічних і теоретичних положень розробляти теорію їх проектування у відповідності з принципами системного підходу. За ступенем інтелектуалізації СПР можна поділити так:

· системи перебору варіантів рішень згідно з встановленою пріоритетністю для наперед змодельованих ситуацій;

· СПР, які приймають рішення за детермінованими вирішальними правилами без навчання;

· СПР, що реалізують алгоритми компараторного розпізнавання за еталонами;

· експертні системи, що з метою прийняття ефективних рішень маніпулюють спеціальними знаннями, накопиченими фахівцями-експертами у конкретно-предметній області знань;

· СПР, що навчаються;

· знання-орієнтовані (knowledge-based) СПР, що здатні утворювати базу знань;

Здатні навчатися СПР можна поділити на такі основні класи:

· СПР, що розв’язують задачу розпізнавання образів за апріорно класифікованою навчальною матрицею (навчання з “учителем”);

· СПР, що реалізують алгоритми факторного класифікаційного аналізу ;

· СПР, що реалізують алгоритми кластер-аналізу при незмінному словнику ознак і за апріорно некласифікованими навчальними матрицями, тобто за умови неповної апріорної інформації про функціональний стан системи (навчання без “учителя”);

· СПР, що самонавчаються, які реалізують алгоритми автоматичної класифікації за апріорно некласифікованими навчальними матрицями, але здатні оптимізувати параметри словника ознак розпізнавання ;

· відмовостійкі СПР, що здатні самостійно діагностувати свій функціональний стан і відновлювати свою функціональну спроможність при виникненні відмов;

· адаптивні СПР, що здійснюють класифікаційне самонастроювання та самоорганізацію системи;

· томографічні СПР, що відновлюють щільність перерізу об’єкту за його проекціями;

· СПР, що вирішують проблему шкалювання, яка полягає в побудові для шкал з різними мірами виміру зведеної шкали, координати якої можуть бути обернено відображені на відповідні вихідні шкали;

· сенсорні СПР, що моделюють чуттєві функції людини і комплекс технічних засобів (КТЗ) яких базується на “образному” комп’ютері, наділеному властивостями “технічного зору”, усномовного розпізнавання, розпізнавання пахощів та інше;

· гібридні СПР, які поєднують різні алгоритми та методи автоматичної класифікації.

До знання-орієнтованих СПР за сучасною класифікацією відносяться:

· системи, що ґрунтуються на інструктивних знаннях (rulebased reasoning);

· системи, що ґрунтуються на автоматичному доведенні теорем (automatic theorem-proving techniques);

· системи, що ґрунтуються на автоматичному породженні гіпотез (automatic hypothesizing);

· системи, що ґрунтуються на доведенні за аналогією (analogical reasoning);

· об’єктно-орієнтовані інтелектуальні системи (object-oriented intelligent systems);

· об’єктно-логічні інтелектуальні системи, що поєднують окремі переваги об’єктно-орієнтованих систем з системами автоматичного доведення теорем і використовують об’єктно-логічні мови, фреймові логіки (F-logics), логіки транзакції (transaction logics) та інше.

Зрозуміло, що наведена класифікація не є досить повною, оскільки відбувається неперервне розширення номенклатури СПР як за призначенням, так і за принципами функціонування.

Існують такі основні підходи до аналізу та синтезу СПР:

· алгебраїчний;

· теоретико-статистичний;

· геометричний;

· структурний (лінгвістичний);

· біонічний (нейромережний);

· мережний;

· нечіткий;

· теоретико-ігровий.

Незважаючи на те, що наведені підходи відрізняються один від одного рівнем і видом математичної формалізації слабо формалізованих процесів прийняття рішень, між ними не існує чіткої межі, а самі підходи часто доповнюють один одного. Оскільки всі основні підходи, окрім алгебраїчного, перетинаються з геометричним, то саме в рамках геометричного підходу формування загальної теорії прийняття рішень є найбільш виправданим.

1.2. Структура та функції СПР

На рис. 1.2.1 показано узагальнену функціональну схему здатної навчатися СПР. Тут функціональні блоки, що знаходяться зверху пунктирної лінії, відносяться безпосередньо до СПР. Показана на рис. 1.2.1 структура СПР дозволяє функціонувати системі у режимах як навчання, так і екзамену.

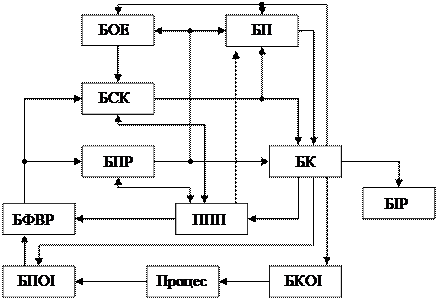
Рисунок 1.2.1 – Узагальнена функціональна схема СПР,

що навчається

Робота системи в режимі навчання регламентується програмно блоком керування (БК), який при кожному випробуванні видає команду на блок кінцевої обробки інформації (БКОІ) для вироблення ініціюючої дії на виконавчі органи. Блок первинної обробки інформації (БПОІ) перетворює інформацію про функціональний стан процесу керування до вигляду, зручного для подальшого оброблення ЕОМ, і передає її у блок формування векторів розпізнавання (БФВР), що є автоматом допускового контролю. Із пристрою постійної пам’яті (ППП) у БФВР за командами БК надходять значення контрольних допусків на ознаки розпізнавання, які порівнюються із виміряними значеннями відповідних ознак. У результаті кожного випробування на виході БФВР формується структурований випадковий двійковий вектор-реалізація образу, координати якого є предикатами, що приймають значення "1", якщо значення відповідної ознаки знаходиться в полі контрольних допусків, і "0", якщо - не знаходиться.

Вектор-реалізація образу надходить у блок прийняття рішень (БПР), де визначається його належність деякому класу розпізнавання, і в блок статистичної корекції (БСК), який визначає оптимальні значення параметрів функціонування СПР шляхом пошуку максимуму КФЕ навчання системи розпізнавати реалізації відповідного образу. КФЕ обчислюється блоком оцінки ефективності (БОЕ).

Режим екзамену виконується безпосередньо в робочому режимі функціонування системи. При цьому БСК і БОЕ не функціонують, але може підключатися блок прогнозування (БП), призначений для прогнозування зміни функціонального стану СПР. Для спостереження і реєстрації інформації служить блок індикації і реєстрації (БІР).

Таким чином, розглянута структура СПР має широкі функціональні можливості, що дозволяє розв’язувати широкий клас задач автоматичної класифікації, включаючи і задачу прогностичної класифікації.

1.3 Види забезпечення СПР

Згідно з існуючим стандартом [4] для СПР, що навчається, доцільним є виділення таких основних видів її забезпечення, як технічне, інформаційне, програмне та організаційне, структуру яких показано на рис. 1.3.1.

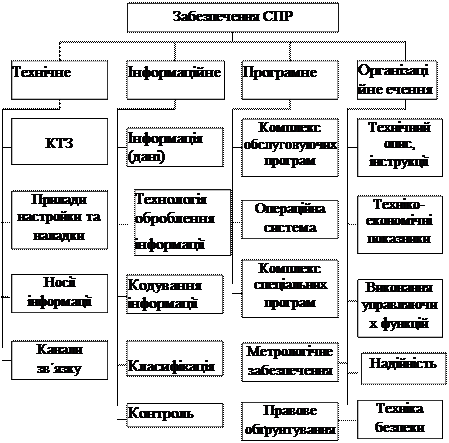
Рисунок 1.3.1 - Види забезпечення СПР, що навчається

Технічне, загальне програмне й організаційне забезпечення, у силу їх інваріантості до функціональних характеристик СПР, що навчаються, суттєво не відрізняються за структурою від відповідних видів забезпечення для автоматизованих систем керування різного призначення. Це обумовлено використанням в СПР типових КТЗ, стандартних програм і операційних систем, які випускаються світовими розробниками засобів автоматизації і комп’ютерних систем, та усталеними нормами їх експлуатації та супроводу.

На ефективність функціонування СПР, що навчаються, вирішальний вплив має інформаційне забезпечення, яке характеризується значним обсягом інформаційних операцій, пов’язаних на етапі навчання із структуруванням і нормалізацією даних, управлінням масивами даних, оцінкою ефективності процесу навчання, формуванням і веденням інформаційного фонду та прийняттям рішень на екзамені. Тому при алгоритмічному підході доцільно вважати математичне забезпечення, яке включає методи і алгоритми виконання інформаційних і обчислювальних процедур, спрямованих на формування та перетворення інформаційних структур даних, складовою частиною інформаційного забезпечення. Таким чином, математичне забезпечення СПР, що навчається, розглядається як технологія оброблення інформації з метою прийняття достовірних рішень про функціональний стан системи. На рис. 1.3.2 подано структуру інформаційного забезпечення СПР, що навчається, основними елементами якого є:

· інформація як атрибут прийняття рішень;

· технологія оброблення інформації як формалізована система обчислювальних і логічних операцій, що виконуються у процесі отримання, передачі, зберігання та оброблення інформації;

· кодування як спосіб інформаційного узгодження елементів КТЗ, стиснення інформації, підвищення її завадозахищеності та безпеки;

· класифікація як процес прийняття рішень;

· контроль як процес установлення відповідності між функціональними станами СПР.

Технологія оброблення інформації включає як інтегруюче середовище, так і систему обчислювальних та логічних операцій, які виконуються ЕОМ в рамках визначеного алгоритму.

Однією із важливих функцій інформаційного забезпечення є класифікаційний аналіз даних, який на рис. 1.3.2 показано як окремий елемент інформаційного забезпечення.

Розробка інформаційного забезпечення СПР, що навчається, складається з послідовного розв’язання таких основних задач:

· організація збору інформації про можливі функціональні стани та режими функціонування СПР;

· формування словника ознак розпізнавання;

· розробка математичної (інформаційної) моделі СПР для режимів її функціонування;

· конструювання КФЕ навчання СПР і розробка процедури його обчислення;

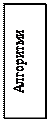· розробка засобів інформаційних технологій прийняття достовірних рішень за умови апріорної невизначеності;

· вибір оптимальних допустимих рішень на екзамені;

· розробка методу та алгоритмів перспективного та нормативного прогнозування функціональної ефективності та надійності СПР, що навчаються.

Розв’язання наведених вище задач інформаційного забезпечення дозволяє отримати відповіді на такі важливі питання, як інформаційне відображення функціональних станів СПР, що навчається, реалізація розвідувального аналізу з метою формування умов і оцінки статистичної стійкості та однорідності навчальної вибірки, визначення мінімального обсягу репрезентативної навчальної вибірки, формування вхідного математичного опису, оцінка функціональної ефективності системи і розробка математичних моделей процесу навчання та алгоритмів оптимізації просторово-часових параметрів функціонування за КФЕ навчання з метою забезпечення на екзамені достовірної класифікації поточного або спрогнозованого функціональних станів системи.

1.4 Проблема синтезу СПР

Залежно від вхідних даних і уявлень про побудову та функціонування системи задачі синтезу поділяються на три класи [3]:

· інформаційний синтез, який передбачає оптимізацію (тут і далі в інформаційному розумінні) функціональної ефективності системи;

· структурний синтез, який спрямований на оптимізацію складу, конфігурації, внутрішніх і зовнішніх зв’язків системи при заданих алгоритмах її функціонування;

· комбінований синтез структури та алгоритмів функціонування, пов’язаний з розподілом функцій за елементами системи та визначенням їх оптимального складу.

Необхідною умовою синтезу системи є наявність вхідного математичного опису.

Визначення 1.4.1. Вхідний математичний опис є адекватною моделлю вхідних даних, що відбивають основні характеристики та властивості функціонального стану системи.

Визначення 1.4.2. Під функціональним станом розуміються основні характеристики системи у визначений момент або інтервал часу її функціонування у заданому режимі, які залежать як від технічного стану системи, так і від середовища, що впливає на неї через контрольовані і неконтрольовані фактори.

Оскільки система повністю визначається шляхом однозначного завдання її елементів, відношень і властивостей, то задача синтезу полягає у цілеспрямованому виборі цих категорій, які забезпечують ефективне функціонування системи.

Визначення 1.4.3. Метою синтезу системи є конкретизація та визначення таких значень і співвідношень її категорій як елементи, відношення та властивості, що дозволяють системі функціонувати із визначеною ефективністю.

Оскільки поняття “ефективність” все ще залишається неформалізованим, тому пропонується таке її визначення.

Визначення 1.4.4. Загальна ефективність системи визначає ступінь відповідності її складових виконанню системою свого призначення згідно з критерієм мети.

Важливою складовою загальної ефективності є функціональна ефективність.

Визначення 1.4.5. Під функціональною ефективністю системи розуміється складова загальної ефективності, яка визначає ступінь відповідності функціонування системи за її робочим алгоритмом виконанню поставленої перед нею задачі згідно з поставленою цілью.

Проблема синтезу СПР містить такі задачі [12]:

· формування цілі;

· визначення властивостей системи;

· визначення множини допустимих рішень;

· формування критеріїв оцінки допустимих рішень;

· вибір оптимального рішення.

Визначення 1.4.6. Ціль – це деякий бажаний стан СПР, досягнення якого вимагає спеціально організованих дій.

Формування цілі є неформалізованим процесом і здійснюється як правило на професійно-мовному рівні шляхом встановлення функціональної залежності узагальненої ефективності системи від множини формалізованих властивостей. Принципові ускладнення при розв’язанні цієї задачі обумовлені необхідністю побудови шкали виміру «ефективність-вартість», де під вартістю мається на увазі зведена вартість всіх показників системи. У праці [9] І.В. Кузьмін запропонував узагальнену ефективність складної системи визначати за двома складовими: інформаційна спроможність системи та зведена вартість створення, експлуатації, зберігання та ліквідації системи. Тоді узагальнений функціонально-статистичний критерій ефективності має такий вигляд:

Е_I,C = К_I / К_I0 , (1.4.1)

де К_I – узагальнена функціонально-статистична характеристика дійсної системи:

К_I =I_max/C.

Тут I_max - максимальна інформаційна спроможність системи; C– зведені витрати на створення, експлуатацію та ліквідацію системи. Узагальнена функціонально-статистична характеристика потенційної (ідеальної) системи тут визначається як

К_I0 = / C_min ,

де - максимальна інформаційна спроможність потенційної системи; C_min - зведені витрати для потенційної системи.

Потенційна система повинна відповідати таким умовам:

· апріорні (безумовні) гіпотези є рівноймовірними, оскільки потенційна система повинна приймати рішення в найгірших у статистичному розумінні умовах;

· умовні ймовірності прийняття гіпотези g_l при появі події m_m, де , розподілені за нормальним законом, при якому інформаційна міра є максимальною.

Використання узагальненого критерію (1.4.1) є доцільним на етапі апріорного моделювання, коли оцінюється ступінь близькості системи, що проектується, до деякої гіпотетичної ідеальної, тобто потенційної системи. Виправданим є застосування критерію (1.4.1) і при структурному синтезі системи, де, як правило, використовуються вартісні показники. При цьому має місце подвійність розв’язання цієї задачі:

1) Задана нижня допустима межа ефективності системи. Потрібно синтезувати систему із заданою ефективністю та мінімальною вартістю.

2) Задана верхня межа вартості системи. Потрібно синтезувати систему із максимальною ефективністю, але не дорожче заданої вартості.

На етапі апостеріорного моделювання найбільшої актуальності набуває оцінка функціональної ефективності системи, тому вартісна складова критерію ефективності може не розглядатися.

Формування критерію мети спрямовано на зняття невизначеності в описі системи. Оскільки мірою невизначеності є кількість інформації, то критерій мети має інформаційну природу, а інформаційний критерій функціональної ефективності (КФЕ) системи є його важливою складовою, яка визначає асимптотичні точнісні характеристики класифікатора.

Завершальним етапом інформаційного синтезу СПР є вибір оптимального рішення із множини допустимих рішень Х шляхом пошуку в робочій (допустимій) області визначення G глобальних екстремумів обраних частинних КФЕ:

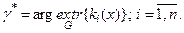(1.4.2)

Якщо 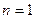, то задача вибору оптимального рішення є однокритеріальною і вона має єдине рішення. Якщо 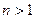, то задача багатокритеріальна і в загальному випадку вона не має єдиного рішення.

1.5. Структура множини допустимих рішень [12]

У загальному випадку множина допустимих рішень 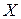є композицією двох підмножин: погоджених рішень (області згоди 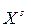) і компромісних рішень (області компромісів ).

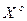Визначення 1.5.1.Областю згоди X^s називається підмножина множини допустимих рі­шень X, в якій один або кілька частинних критеріїв можна поліпшити без погіршення якості інших частинних критеріїв.

Визначення 1.5.2.Областю компромісів X^c називається підмножина X, в якій жодний частинний критерій к_i(х) неможливо поліпшити без погіршення значення хоча б одного іншого частинного критерію. Таку підмножину часто називають областю Парето або множиною Парето-оптимальних рішень.

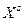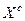Для підмножин і виконуються умови

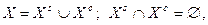(1.5.1)

які означають, що об'єднання підмножин утворює допустиму множину і будь-яке рішення х 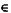X належить тільки одній з підмножин.

Для випадку двох критеріїв 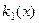і 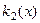, кожний з яких максимізусться, загальну структуру допустимої множини X показано на рис. 1.5.1. В окремих випадках множина X може складатися тільки з області згоди 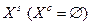(рис. 1.5.2) або компромісу 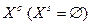(рис. 1.5.3).

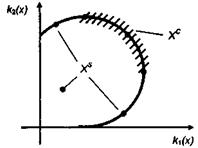
Рисунок 1.5.1– Загальна структура множини X

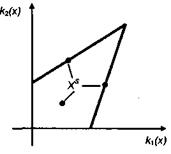
Рисунок 1.5.2 – Приклад множини X, що складається тільки з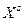

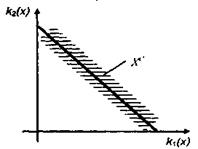
Рисунок 1.5.3 – Приклад множини Х, що

складається тільки з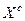

За визначенням 1.5.1 область згоди 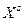взагалі не може містити екстремальних рішень, тому що кожне 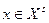можна поліпшити хоча б за одним критерієм. Тому розв'язок задачі (1.4.2) збігається з областю компромісів 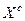, і якщо вона не порожня, тобто 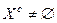, то усі 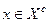є роз­в'язками задачі. Отже, задача багатокритеріальної оптимізації (1.4.2) має єдиний розв'язок тільки тоді, коли 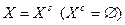. У протилежному випадку розв'язок не єдиний. Це означає, що задача є некоректно поставленою за Адамаром.

Визначення 1.5.3. Коректними за Адамаром називаються задачі, для яких існує єдиний стійкий розв'язок, тобто в заданій метриці малим варіаціям вхідних змінних відповідають малі варіації вихідних змінних.

Невиконання хоча б однієї з перелічених умов робить задачу некоректною. Так, якщо множина Х містить область компромісів 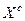, задача (1.4.2) є некоректною за другою ознакою.

У загальному випадку некоректну задачу можна звести до коректної введенням деяких додаткових співвідношень, що називаються регуляризуючими правилами. При розв'язанні задачі багато-критеріальної оптимізації (1.4.2) таким регуляризуючим правилом є схема компромісу, що визначає правило вибору з множини 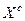єдиного "компромісного" за значенням частинних критеріїв рішення. Саме ця обставина визначила назву множини 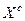. Існують два підходи до вибору єдиного рішення з області компромісів 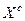: формальний (конструктивний) і евристичний.

У першому випадку визначається формальне регуляризуюче правило – схема компромісів, що гарантує вибір рішення х 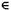X такого, що 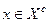. У другому випадку вибір єдиного рішення здійснюється "особою, що приймає рішення" (ОПР) на основі інтуїтивних, евристичних (неформаль­них) міркувань. При цьому ОПР – це людина або група людей (колективний орган), які уповноважені приймати рішення. Як правило, підготовку рішень здійснює експерт-фахівець (фахівці), що аналізує рішення, може давати поради, але не має повноважень приймати рішення. При реалізації евристичного підходу до вибору компромісного рішення обов'язковим етапом підготовки рішень експертом є виділення з допустимої області рішень X області компромісів 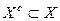, оскільки тільки в ній знаходяться ефективні рішення. Для формальних схем вибору компромісних рішень ця процедура не є обов'язковою, тому що більшість таких схем гарантує вибір рішень 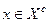, але часто є бажаною з обчислювальних міркувань.

Розглянемо математичні моделі визначення області компромісів 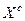на множині допустимих рішень X.

Математична модель визначення точної області компромісів.Існує декілька моделей визначення X^c, але найбільш відомою і строгою є модель Ю. Гермейєра:

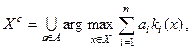(1.5.2)

де а =<а₁, а₂,..., а_n > – безрозмірні вагові коефіцієнти частинних критеріїв k_і (х), які є визначеними на множині

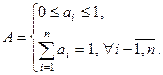(1.5.3)

Задача зводиться до визначення екстремумів лінійного функціонала 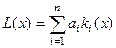при різних а 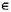А. Об'єднання цих екстремальних рішень утворює область компромісів, показану на рис. 1.5.4. Розглянута модель є правильною тільки тоді, коли множина X є опуклою. У протилежному разі слід використовувати інші, більш складні моделі.

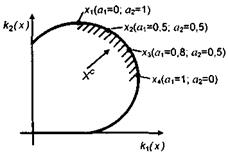
Рисунок 1.5.4 – Формування області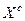

Зазначені недоліки можна подолати, якщо визначати не точну, а наближену область компромісів.

Визначення наближеної області компромісів.Процедура побудови наближеної області компромісів 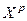полягає у визначенні не всієї множини точок 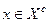, а тільки рішень, які визначають межу області. Умовою коректності такої процедури є

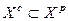, (1.5.4)

тобто повне включення точної області компромісів у наближену. Один із можливих методів розв'язування цієї задачі є таким. На множині допустимих рішень X послідовно розв'язуються п одно-критеріальних оптимізаційних задач за кожним частинним критерієм :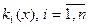

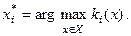(1.5.5)

Для цього в моделі (1.5.2) досить покласти а_i= 1 і тоді відповідно до (1.5.3) всі інші коефіцієнти дорівнюватимуть нулю. Для кожного рішення 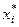обчислюються значення всіх інших частинних критеріїв, які позначимо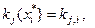 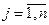. Отримані результати заносяться в таблицю для розрахунків наближеної області компромісів 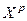. Кожну строку цієї таблиці утворюють значення i-го частинного критерію у точках екстремуму за всіма іншими частинними критеріями. Наприклад, перший рядок містить значення критерію k₁(x) у точ­ках 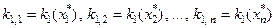, де 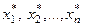– рішення, екстремальні за відповідними критеріями. Зрозуміло, що екстремальне значення кожного частинного критерію досягається на головній діагоналі.

У кожному рядку значення частинного критерію k_i(х) змінюються від екстремального 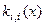(найкращого) до найгіршого. Множини цих значень за всіма 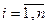є межами відображення наближеної області компромісів 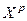на простір критеріїв K = {k_i (х)}, 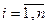. Наближена область компромісів 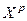у просторі частинних критеріїв задається обмеженнями:

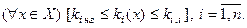(1.5.6)

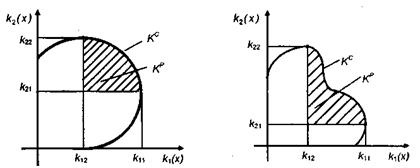
Вигляд відповідної обмеженням (1.5.6) наближеної області компромісів для опуклої і неопуклої множини X відповідно показано на рис. 1.5.5.

а) б)

Рисунок 1.5.5– Наближена область компромісів: а) на опуклій множині Х; б) на неопуклій множині Х

Область 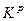містить у собі область 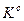, тому що вона утворена екстремальними значеннями всіх частинних критеріїв, що, як випливає з (1.5.2), є достатньою умовою. Водночас наближена область більша за область компромісів, оскільки містить у собі, як видно з рис. 1.5.5, частину області згоди.

1.6 Запитання та завдання для самопідготовки

1. Чим відрізняється цілеспрямована система від нецілеспрямованої?

2. Чим відрізняється експертна система від системи підтримки прийняття рішень?

3. Якими функціональними властивостями відрізняється адаптивна СПР від неадаптивної?

4. Чим відрізняється кластер-аналіз від класифікаційного факторного аналізу?

5. Чим відрізняється самонавчання від кластер-аналізу?

6. У чому полягає проблема шкалювання?

7. Що називається сенсорними СПР?

8. Який із підходів до синтезу СПР, що навчаються, слід розглядати як універсальний?

9. Що називається областю згоди?

10. Що називається областю компромісів?

11. Чим відрізняється однокритеріальна задача прийняття рішень від багатокритеріальної?

12. Покажіть графічно випадок, коли множина допустимих рішень складається тільки з області згоди.

13. Покажіть графічно випадок, коли множина допустимих рішень складається тільки з області компромісів.

14. Які існують підходи до вибору єдиного рішення з області компромісів?

15. Яка процедура дозволяє визначити точну область компромісів?

16. Доведіть, що наближена область компромісів більша за точну область компромісів.