Мультиплексор как многофункциональный узел
Все цифровые комбинационные узлы являются многофункциональными, то есть они могут выполнять функции, специально для них не предусмотренные. В ряде случаев эти узлы обеспечивают некоторые схемные преимущества перед специализированными, предназначенными для реализации этих функций. Мультиплексор является наиболее характерным многофункциональным узлом.
1. Использование мультиплексора по прямому назначению [1]. В качестве примеров можно привести следующие: мультиплексирование многоразрядного адреса микросхем памяти; мультиплексное управление многоразрядными многоэлементными индикаторами [12]; последовательный опрос многих переменных, датчиков и других однобитовых источников информации; временное уплотнение аналоговых сигналов в телефонии; мультиплексирование выходных данных тестопригодных БИС; построение многоканальных коммутаторов, осциллографов.
2. Реализация произвольных функций алгебры логики на мультиплексорах. Пусть требуется реализовать ФАЛ, зависящую от двух переменных и представленную таблицей истинности (табл. 1). Запишем обобщенную форму СДНФ для этой функции и одновременно уравнение для MS 4®1:
Yфал = x1x0 .1+x1x0 .0+x1x0.0+x1x0.1 (1)
YMS = a1a0.D0+a1a0.D1+a1a0.D2+a1a0.D3 (2)
Таблица 1
| N набора | х1 | х0 | y |
Очевидно полное совпадение выражений (1) и (2), из которых следует: если логические переменные x1 и x0 подать на соответствующие адресные входы а1 и а0 MS 4®1, то на его информационные входы D0, D1, D2 и D3 нужно подать соответственно 1, 0, 0 и 1 (рис. 1).
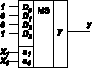
Рис. 1
В общем случае можно сформулировать следующее правило: если количество логических переменных n, от которых зависит реализуемая ФАЛ, совпадает с разрядностью адресной части мультиплексора, то эти переменные подаются на адресные входы мультиплексора (старшая переменная — на старший адресный вход), а на информационные входы мультиплексора MS 2n®1 — константы 0 и 1 в соответствии с таблицей истинности реализуемой ФАЛ.
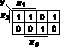
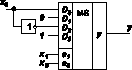
Рис.2 Рис.3
Реализуем на том же MS 4®1 ФАЛ, зависящую от трех переменных (табл. 2). Запишем для нее минимальную дизъюнктивную нормальную форму (МДНФ), воспользовавшись картой Карно, представленной на рис. 2.
Таблица 2
| N набора | x2 | x1 | x0 | y |
y = x2x1x0+x2x0+x2x1 (3)
Преобразуем выражение (3) к виду, аналогичному выражению (1):
y = x2x1.x0+x2x1.0+x2x1 .x0+x2x1.1, (4)
где произведение x2x1.0 введено, чтобы в выражении (4) были представлены все четыре конституенты единицы двух переменных x2 и x1. Сравнивая выражения (4) и (2), опять видим их полное соответствие. Отсюда вывод: на адресные входы а1 и а0 MS 4®1 нужно подать логические переменные x2 и x1, а информационные входы D0, D1, D2 и D3 для произвольной ФАЛ, зависящей от трех переменных, в общем случае являются функциями от третьей переменной x0. Такими функциями являются 0, 1, x0 и x0. Реализация данной ФАЛ представлена на рис. 3. Тот же результат проще получить, если в табл. 2 выделить четыре группы по две строки в каждой и отделить переменную x0 от x2 и x1 (табл. 3).
Таблица 3
| N набора | x2 | x1 | x0 | y |
| 0 1 | 0 0 | 0 0 | 0 1 | 0 1 |
| 2 3 | 0 0 | 1 1 | 0 1 | 0 0 |
| 4 5 | 1 1 | 0 0 | 0 1 | 1 0 |
| 6 7 | 1 1 | 1 1 | 0 1 | 1 1 |
Видно, что переменные x2 и x1 образуют четыре набора, на каждом из которых функция y зависит только от одной переменной x0, причем значения y = f(x0) легко выявляются из этой таблицы.
Для общего случая можно сформулировать следующее правило: если количество логических переменных n, от которых зависит реализуемая ФАЛ, на единицу больше разрядности адресной части мультиплексора, то данную ФАЛ можно реализовать на мультиплексоре MS 2n®1 и одном инверторе.
Если распространить данный метод на реализацию ФАЛ, зависящую от четырех переменных, на том же MS 4®1, то очевидно, что если две старшие переменные x3 и x2 подать соответственно на адресные входы а1 и а0, то информационные входы будут функциями двух младших переменных x1 и x0. Всего таких функций 16, из них 6 — вырожденные (0, 1, x1, x0, x1, x0), а 10 функций зависят от двух переменных, причем для реализации последних требуются 8 различных логических элементов (И, И-НЕ, ИЛИ, ИЛИ-НЕ, аb — элемент запрета, а+b — элемент, реализующий функцию импликации, аb+аb — элемент равнозначности и аb+аb — элемент, реализующий сумму по модулю два [2]. Итак, кроме мультиплексора, данная реализация потребует в худшем случае восемь различных логических элементов, поэтому ее, как правило, не рекомендуется использовать.
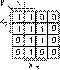
Рис. 4
В некоторых частных случаях ФАЛ, зависящую от четырех переменных, можно реализовать с использованием только одного мультиплексора MS 4®1 без каких либо логических элементов. Рассмотрим эти случаи. Пусть требуется реализовать ФАЛ, представленную картой Карно (рис. 4). Если две старшие переменные x3 и x2 подать на адресные входы а1 и а0 MS 4®1, то информационные входы D0, D1, D2 и D3 можно представить четырьмя картами Карно для двух переменных x1 и x0 (рис. 5). Эти карты являются в данном случае строками карты Карно, представленной на рис. 4. Из рис. 5 следует: D0 = x1x0, D1 = x0, D2 = x1+x0 и D3 = x1. Соответствующая реализация показана на рис. 6.
Подадим теперь на адресные входы а1 и а0 соответственно переменные x1 и x0, тогда информационные входы D0, D1, D2 и D3 можно представить четырьмя картами Карно для двух переменных x3 и x2 (рис. 7), причем эти карты в данном случае — столбцы карты Карно, данной на рис. 4. Из рис. 7 следует: D0 = 0, D1 = x2, D2 = 1 и D3 = x3. Соответствующая реализация — на рис. 8. Сравнивая рис. 6 и 8, делаем очевидный вывод о предпочтительности реализации, представленной на рис. 8, так как здесь не требуется никаких логических элементов.
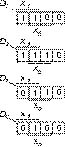
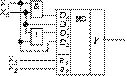
Рис. 5 Рис.6
Поиск рациональной структуры по данной методике в общем случае потребует анализа шести вариантов подачи двух различных переменных из четырех на адресные входы MS 4®1 (здесь шесть — это число различных сочетаний из четырех переменных по две). Проще рациональную структуру выявить, выполняя следующие процедуры:
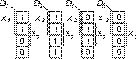
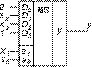
Рис.7 Рис.8
- Записать реализуемую ФАЛ в МДНФ. В нашем случае из рис. 4 следует:
y = x3x1+x1x0+x2x0 (5)
- Определить две переменные, наиболее часто встречающиеся в различных простых импликантах. В нашем случае это x1 и x0, так как они встречаются по два раза, а переменные x3 и x2 только один. Именно переменные x1 и x0 необходимо подать на соответствующие адресные входы а1 и а0 MS 4®1.
- Используя правило развертывания, законы дополнительности, одинарных элементов, поглощения и распределительный закон первого рода [3], преобразовать МДНФ к виду, когда в выражении для реализуемой ФАЛ присутствуют все четыре конституенты единицы двух переменных, выявленных в предыдущей процедуре. В нашем случае имеем:
y = x3x1+x1x0+x2x0 = x3x1.1+x1x0+x2.1.x0 =
x3x1(x0+x0)+x1x0+x2(x1+x1)x0 =
x3x1x0+x3x1x0+x1x0 +x2x1x0+x2x1x0 =
x2x1x0+x3x1x0+x1x0(1+x3+x2) =
x2x1x0+x3x1x0+x1x0 (6)
Представим теперь выражение (6) в виде, аналогичном выражению (1):
y = x1x0 .0+x1x0 .x2+x1x0 .x3+x1x0 .1 (7)
Сравнивая (7) и (2), выявляем: D0 = 0, D1 = x2, D2 = x3 и D3 = 1 (рис. 8). Эту методику можно распространить и на реализацию систем двух или четырех ФАЛ с использованием 2- или 4-разрядных мультиплексоров, имеющих общую адресную часть. Рациональный выбор переменных, подаваемых на адресные входы мультиплексоров, определяются подсчетом общего числа каждой переменной, входящей в две или четыре функции, и в качестве адресных выбираются те, которые встречаются наибольшее число раз во всех простых импликантах всех реализуемых ФАЛ.

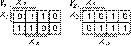
Рис.9 Рис.10
Если использовать стробируемые MS 2n®1, имеющие три состояния выхода, то любую ФАЛ, зависящую от n+2 переменных, легко реализовать на двух стробируемых мультиплексорах и двух инверторах. Один из инверторов используется в цепи стробирования одного из мультиплексоров, другой — на их информационных входах. Рассмотрим пример. Пусть ребуется реализовать ФАЛ, представленную картой Карно на рис. 9, на стробируемых мультиплексорах MS 4®1, имеющих три состояния выхода и активный уровень 0 на стробирующих входах. Представим эту карту в виде двух, зависящих от трех младших переменных (рис. 10). Подавая переменную x3 непосредственно на стробирующий вход одного из мультиплексоров MS 4®1, мы реализуем функцию y1 (карта Карно, рис. 10а) и через дополнительный внешний инвертор на вход другого — y2 (рис. 10б). Очевидно, что y = y1+y2, причем логическая операция ИЛИ здесь — монтажная операция соединения в единую цепь выходов этих двух мультиплексоров. Подавая переменные x2 и x1 на соответствующие адресные входы а1 и а0, а переменную x0 непосредственно или через второй дополнительный внешний инвертор вместе с константами 0 и 1 на информационные входы мультиплексоров, получаем окончательную реализацию ФАЛ (рис. 11). Отметим, что функции y1 и y2 можно реализовать по рациональным структурам, способы получения которых описаны выше, так как на адресные входы двух мультиплексоров не обязательно подавать одни и те же переменные.
Реализацию одной ФАЛ на мультиплексоре можно рассматривать как одноразрядное ПЗУ, а систем n ФАЛ, зависящих от одних и тех же переменных — как n-разрядное ПЗУ.
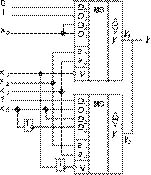
Рис. 11
3. Мультиплексор в режиме сдвигателя. Сдвигателем называется цифровой комбинационный узел, предназначенный для сдвига n-разрядного слова на любое число разрядов в диапазоне от 0 до m за один такт. Имеется в виду, что смена однопозиционного управляющего сигнала вызывает немедленное (через время, определяемое задержками распространения сигналов через логические элементы) выполнение требуемой микрооперации. Рассмотрим уравнения для сдвигателя с параметрами n = 4, m = 3 (разрядность входного слова X n = 4, разрядность выходного слова Y n+m = 7, сдвиг может быть реализован на 0, 1, 2 и максимум на три разряда).
y0 = S0x0
y1 = S0x1+S1x0
y2 = S0x2+S1x1+S2x0
y3 = S0x3+S1x2+S2x1+S3x0 (8)
y4 = S1x3+S2x2+S3x1
y5 = S2x3+S3x2
y6 = S3x3,
где S0 — однопозиционный управляющий сигнал; при его активном состоянии S0 = 1 и S1 = S2 = S3 = 0 обеспечивается передача входного слова на выход без сдвига, при S1 = 1 и S0 = S2 = S3 = 0 осуществляется сдвиг входного слова на один разряд и т. д.
Для реализации этих уравнений требуются двухвходовые элементы И и элементы ИЛИ на 2, 3 и 4 входа. Так как в данном случае выполняется четыре микрооперации (m = 0, 1, 2 или 3), то наиболее просто реализовать такой сдвигатель на семи одноразрядных MS 4®1, используя их адресные входы как управляющий код числа m (табл. 4).
Таблица 4
| N набора | а1 | а0 | m |
Схема такого сдвигателя приведена на рис. 12. На свободные входы мультиплексоров подаются сигналы, характер которых определяется конкретным алгоритмом, реализуемым операционным узлом (логический, арифметический, циклический сдвиг и т. п.)
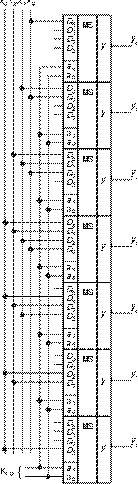
Рис. 12
4. Мультиплексор — преобразователь параллельного кода в последовательный. Схема такого преобразователя приведена на рис. 13. Здесь четырехразрядный параллельный код с выходов регистра подается на информационные входы MS 4®1, адресные входы которого подключены к выходам 2-разрядного счетчика. Если счетчик изменяет свои состояния от тактовых импульсов в последовательности 0, 1, 2, 3, то на выходе мультиплексора появляются разряды слова, начиная с младшего; если как 3, 2, 1, 0, то начиная со старшего. Варианты схем, использующих эту структуру, чрезвычайно разнообразны.
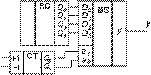
Рис. 13
5. Мультиплексор в составе многоканального селектора. Многоканальным селектором называется цифровой комбинационный узел, имеющий n входов и m выходов, с возможностью передачи данных с любого входа в любой выход при использовании между входами и выходами минимального числа линий связи. Рассмотрим конкретную схему для случая n = m = 8. Общая идея: из 8 входов передадим данные в одну линию с помощью мультиплексора, а затем из этой линии передадим данные на 8 выходов с помощью однобитового селектора. Схема приведена на рис. 14, где обозначено: src (source) — источник, dst (destination) — приемник, А — адрес источника, В — адрес приемника. В качестве однобитового селектора используется двоично-десятичный дешифратор с активным нулем на выходах. При А = В реализуется алгоритм передачи данных scri ® dsti, а при А = В — scri ® dstj, i = 0...7, j = 0...7.
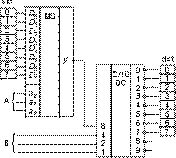
Рис. 14
6. Мультиплексор в составе компаратора двух чисел, вырабатывающего осведомительный сигнал А = В. Если в распоряжении разработчика нет специализированного компаратора, то его можно реализовать, используя совместно дешифратор и мультиплексор. Определение, структура и применение специализированного компаратора будут рассмотрены в следующей статье учебного цикла. На рис. 15 приведена схема компаратора, сравнивающего два 3-разрядных числа. В ней используются дешифратор “1 из 8” с активной единицей выхода и мультиплексор MS8®1 с прямым выходом. При А = В активная единица с выхода дешифратора передается на выход мультиплексора и, следовательно, Fa=b= 1. При А = В на выход будет передаваться сигнал 0 (Fa=b= 0). Рекомендуется самостоятельно реализовать компаратор двух 2-разрядных чисел, используя один MS 8®1 и один инвертор (см. раздел 2 данной статьи).
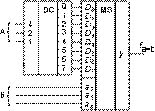
Рис. 15
7. Мультиплексор в составе контроллера состояния сложного объекта. Постановка задачи: пусть сложный цифровой блок разбит на 8 функционально законченных узлов — источник вторичного питания, операционный блок, память, система синхронизации, устройство управления и т. д. Каждый из этих узлов снабжен встроенной системой контроля работоспособности. Если узел исправен, то система контроля выставляет осведомительный сигнал 1, если нет — 0. Требуется быстро определить неработоспособный узел и заменить его. Схема контроллера, выполняющего поставленную задачу, приведена на рис. 16, где обозначено: G — генератор тактовых импульсов, СТ — трехразрядный суммирующий счетчик, DC — дешифратор “1 из 8”, в качестве дисплея используется один 7-сегментный индикатор.
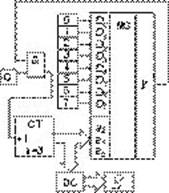
Рис. 16
Если все функциональные узлы 0...7 в порядке, то независимо от адреса мультиплексора y = 1, вентиль И открыт, счетчик циклически изменяет свои состояния, дешифратор их дешифрирует и при частоте генератора более 200 Гц на индикаторе светится с половинной яркостью символ 8, указывающий на полную работоспособность цифрового блока. Пусть в какой-то момент времени узел с номером 6 обнаружил, что он неисправен, и на нем выставляется осведомительный сигнал 0. Как только счетчик примет состояние 6, на выходе мультиплексора появится сигнал 0, который запрет вентиль И. Счетчик останется в том же состоянии, а на 7-сегментном индикаторе высветится 6. После замены узла 6 на индикаторе снова появится символ 8.
8. Мультиплексор MS 2-1 в качестве тактируемого потенциалом D-триггера. Уравнение MS2-1 имеет вид:
y = a0D0 + a0D1 (9)
Характеристическое уравнение тактируемого потенциалом D-триггера с активной единицей на тактовом входе имеет вид:
Qt+1 = Ct+1Qt + Ct+1Dt, (10)
и с активным нулем на тактовом входе:
Qt+1 = Ct+1Dt + Ct+1Qt (11)
где индекс t соответствует текущему состоянию сигналов (до переключения), а t+1 — следующему после переключения. Полагая в уравнении (9) y = Qt+1, D0 = Qt, D1 = Dt и a0 = Ct+1, получаем выражение Qt+1 = Ct+1Qt + Ct+1Dt, полностью совпадающее с уравнением (10).
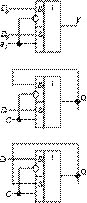
Рис. 17
Полагая в уравнении (9) y = Qt+1, D0 = Dt, D1 = Qt и a0 = Ct+1, получаем выражение Qt+1 = Ct+1Dt + Ct+1Qt, полностью совпадающее с (11). Итак, на одном и том же MS 2®1 можно получить схему потенциально управляемого D-триггера с активными нулем или единицей на тактовом входе. Схема MS 2®1 и соответствующие D-триггеры приведены на рис. 17.
9. Мультиплексоры MS 2®1 в качестве сдвигового регистра. Полученные выше D-триггеры являются прозрачными. Этот термин говорит о том, что при активном сигнале на тактовом входе изменения данных на D-входе немедленно передаются на выход. Известно, что на прозрачных D-триггерах с одним и тем же активным сигналом на тактовых входах нельзя построить сдвиговый регистр. Однако, чередуя триггеры с различными активными сигналами на тактовых входах, это возможно, причем сдвиг данных в нем будет осуществляться как фронтом (переходом 01), так и спадом (переходом 10) на тактовом входе [4]. Хорошим примером может служить схема (рис. 18а) регистра, построенная на интегральной схеме счетверенного мультиплексора типа КР1533КП16 (SN74ALS157A), где DR (data right — данные справа) — последовательный вход в младший разряд при сдвиге в сторону старших разрядов. На рис. 18б приведена временная диаграмма работы данного сдвигового регистра.
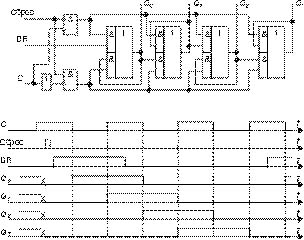
Рис. 18
Примечания к рис. 18а:
1. C = 0 - активный уровень для разрядов Q0 и Q2, C=1 - для Q1 и Q3.
2. Так как отдельно работающие триггеры прозрачны, необходимо помнить: во-первых, обнуление регистра надо осуществлять при С=1, в противном случае при С=0 после снятия сигнала "сброс" (активная единица) разряд Q0 немедленно примет значение сигнала DR; во-вторых, данные на последовательном входе DR надо менять при С=0 (неактивном сигнале для разряда Q0).
3. Как видно из временных диаграмм, данные сдвигаются таким регистром с перекрытием.
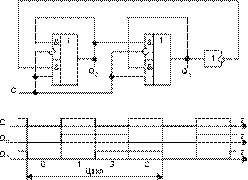
Рис. 19
10. Мультиплексоры в режиме кольцевого счетчика. Кольцевым счетчиком называется сдвиговый регистр, замкнутый в кольцо. Рассмотрим кольцевой 2-разрядный счетчик с одной перекрестной связью (такие структуры называются счетчиками Джонсона). Его схема приведена на рис 19а, а временные диаграммы работы — на рис. 19б. Как видно из временных диаграмм, счетчик имеет четыре состояния в течение двух тактов синхронизации.
Если рассматривать только один выход Q1, то данную схему можно считать счетным триггером, срабатывающим по переходу 10 на входе С, а если только один выход Q0, то ее же можно считать счетным триггером, срабатывающим по переходу 01.
Ограничившись рассмотренными выше простыми схемами применения мультиплексора, перечислим более сложные варианты использования, опубликованные в литературе. В работе [1] рассмотрена структура и возможные режимы работы универсального селектора — мультиплексора типа К561КП2, способного обрабатывать не только цифровые, но и аналоговые сигналы. В [5] показан способ уменьшения емкости памяти с помощью входного мультиплексора. В [6] предложена мажоритарная схема с приоритетом. В [7] рассмотрена схема двоичного шифратора клавиатуры, нечувствительного к “дребезгу” контактов. В [8] предлагается использование мультиплексора для повышения производительности микропроцессора за счет рациональной обработки сигналов запроса на прерывание. В [9] описаны типичные варианты применения программируемого мультиплексора: управление прохождением информации, расшифровка команд микропрограммируемой машины, реализация цифрового хронирующего генератора. В [10] рассматриваются “статистические” или “разумные” мультиплексоры, дающие возможность реализовать в сетях передачи данных многие функции, свойственные более дорогим сетевым процессорам с микропрограммным управлением и концентратором. Другое достоинство статистических мультиплексоров в том, что их распределенная логика позволяет им также работать в качестве модемов и устройств коммутации. В [11] описывается структура цифрового логарифмического преобразователя, который сжимает 8-разрядный двоичный код в 5-разрядный в соответствии с законом 2n® 4n. В [12] подробно рассматривается эффективная адресация жидкокристаллических индикаторов.
Сумматоры: определения, классификация, уравнения, структуры и применение
Основной элементарной операцией, выполняемой над кодами чисел в цифровых устройствах, является арифметическое сложение.
Сумматор — логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. При арифметическом сложении выполняются и другие дополнительные операции: учёт знаков чисел, выравнивание порядков слагаемых и тому подобное. Указанные операции выполняются в арифметическо-логических устройствах (АЛУ) или процессорных элементах, ядром которых являются сумматоры.
Сумматоры классифицируют по различным признакам.
В зависимости от системы счисления различают:
 двоичные;
двоичные;
 двоично-десятичные (в общем случае двоично-кодированные);
двоично-десятичные (в общем случае двоично-кодированные);
 десятичные;
десятичные;
 прочие (например, амплитудные).
прочие (например, амплитудные).
По количеству одновременно обрабатываемых разрядов складываемых чисел:
 одноразрядные,
одноразрядные,
 многоразрядные.
многоразрядные.
По числу входов и выходов одноразрядных двоичных сумматоров:
 четвертьсумматоры (элементы “сумма по модулю 2”; элементы “исключающее ИЛИ”), характеризующиеся наличием двух входов, на которые подаются два одноразрядных числа, и одним выходом, на котором реализуется их арифметическая сумма;
четвертьсумматоры (элементы “сумма по модулю 2”; элементы “исключающее ИЛИ”), характеризующиеся наличием двух входов, на которые подаются два одноразрядных числа, и одним выходом, на котором реализуется их арифметическая сумма;
 полусумматоры, характеризующиеся наличием двух входов, на которые подаются одноимённые разряды двух чисел, и двух выходов: на одном реализуется арифметическая сумма в данном разряде, а на другом — перенос в следующий (более старший разряд);
полусумматоры, характеризующиеся наличием двух входов, на которые подаются одноимённые разряды двух чисел, и двух выходов: на одном реализуется арифметическая сумма в данном разряде, а на другом — перенос в следующий (более старший разряд);
 полные одноразрядные двоичные сумматоры, характеризующиеся наличием трёх входов, на которые подаются одноимённые разряды двух складываемых чисел и перенос из предыдущего (более младшего) разряда, и двумя выходами: на одном реализуется арифметическая сумма в данном разряде, а на другом — перенос в следующий (более старший разряд).
полные одноразрядные двоичные сумматоры, характеризующиеся наличием трёх входов, на которые подаются одноимённые разряды двух складываемых чисел и перенос из предыдущего (более младшего) разряда, и двумя выходами: на одном реализуется арифметическая сумма в данном разряде, а на другом — перенос в следующий (более старший разряд).
По способу представления и обработки складываемых чисел многоразрядные сумматоры подразделяются на:
 последовательные, в которых обработка чисел ведётся поочерёдно, разряд за разрядом на одном и том же оборудовании;
последовательные, в которых обработка чисел ведётся поочерёдно, разряд за разрядом на одном и том же оборудовании;
 параллельные, в которых слагаемые складываются одновременно по всем разрядам, и для каждого разряда имеется своё оборудование.
параллельные, в которых слагаемые складываются одновременно по всем разрядам, и для каждого разряда имеется своё оборудование.
Параллельный сумматор в простейшем случае представляет собой n одноразрядных сумматоров, последовательно (от младших разрядов к старшим) соединённых цепями переноса. Однако такая схема сумматора характеризуется сравнительно невысоким быстродействием, так как формирование сигналов суммы и переноса в каждом i-ом разряде производится лишь после того, как поступит сигнал переноса с (i-1)-го разряда.Таким образом, быстродействие сумматора определяется временем распространения сигнала по цепи переноса. Уменьшение этого времени — основная задача при построении параллельных сумматоров.
Для уменьшения времени распространения сигнала переноса применяют: конструктивные решения, когда используют в цепи переноса наиболее быстродействующие элементы; тщательно выполняют монтаж без длинных проводников и паразитных ёмкостных составляющих нагрузки и (наиболее часто) структурные методы ускорения прохождения сигнала переноса.
По способу организации межразрядных переносов параллельные сумматоры, реализующие структурные методы, делят на сумматоры:
 с последовательным переносом;
с последовательным переносом;
 с параллельным переносом;
с параллельным переносом;
 с групповой структурой;
с групповой структурой;
 со специальной организацией цепей переноса.
со специальной организацией цепей переноса.
Три первых структуры будут подробно рассмотрены в последующих статьях. Среди сумматоров со специальной организацией цепей переноса можно указать:
 сумматоры со сквозным переносом, в которых между входом и выходом переноса одноразрядного сумматора оказывается наименьшее число логических уровней [1];
сумматоры со сквозным переносом, в которых между входом и выходом переноса одноразрядного сумматора оказывается наименьшее число логических уровней [1];
 сумматоры с двухпроводной передачей сигналов переноса [1, 2];
сумматоры с двухпроводной передачей сигналов переноса [1, 2];
 сумматоры с условным переносом (вариант сумматора с групповой структурой, позволяющий уменьшить время суммирования в 2 раза при увеличении оборудования в 1,5 раза) [3];
сумматоры с условным переносом (вариант сумматора с групповой структурой, позволяющий уменьшить время суммирования в 2 раза при увеличении оборудования в 1,5 раза) [3];
 асинхронные сумматоры, вырабатывающие признак завершения операции суммирования, при этом среднее время суммирования уменьшается, поскольку оно существенно меньше максимального.
асинхронные сумматоры, вырабатывающие признак завершения операции суммирования, при этом среднее время суммирования уменьшается, поскольку оно существенно меньше максимального.
Сумматоры, которые имеют постоянное время, отводимое для суммирования, независимое от значений слагаемых, называют синхронными.
По способу выполнения операции сложения и возможности сохранения результата сложения можно выделить три основных вида сумматоров:
 комбинационный, выполняющий микрооперацию “S = A плюс B”, в котором результат выдаётся по мере его образования (это комбинационная схема в общепринятом смысле слова);
комбинационный, выполняющий микрооперацию “S = A плюс B”, в котором результат выдаётся по мере его образования (это комбинационная схема в общепринятом смысле слова);
 сумматор с сохранением результата “S = A плюс B”;
сумматор с сохранением результата “S = A плюс B”;
 накапливающий, выполняющий микрооперацию “S = S плюс B”.
накапливающий, выполняющий микрооперацию “S = S плюс B”.
Последние две структуры строятся либо на счётных триггерах (сейчас практически не используются), либо по структуре “комбинационный сумматор – регистр хранения” (сейчас наиболее употребляемая схема).
Важнейшими параметрами сумматоров являются:
 разрядность;
разрядность;
 статические параметры: Uвх, Uвх, Iвх и так далее, то есть обычные параметры интегральных схем;
статические параметры: Uвх, Uвх, Iвх и так далее, то есть обычные параметры интегральных схем;
 динамические параметры. Сумматоры характеризуются четырьмя задержками распространения:
динамические параметры. Сумматоры характеризуются четырьмя задержками распространения:
 от подачи входного переноса до установления всех выходов суммы при постоянном уровне на всех входах слагаемых;
от подачи входного переноса до установления всех выходов суммы при постоянном уровне на всех входах слагаемых;
 от одновременной подачи всех слагаемых до установления всех выходов суммы при постоянном уровне на входе переноса;
от одновременной подачи всех слагаемых до установления всех выходов суммы при постоянном уровне на входе переноса;
 от подачи входного переноса до установления выходного переноса при постоянном уровне на входах слагаемых;
от подачи входного переноса до установления выходного переноса при постоянном уровне на входах слагаемых;
 от подачи всех слагаемых до установления выходного переноса при постоянном уровне на входах слагаемых.
от подачи всех слагаемых до установления выходного переноса при постоянном уровне на входах слагаемых.
Четвертьсумматор
Простейшим двоичным суммирующим элементом является четвертьсумматор. Происхождение названия этого элемента следует из того, что он имеет в два раза меньше выходов и в два раза меньше строк в таблице истинности по сравнению с полным двоичным одноразрядным сумматором. Наиболее известны для данной схемы названия: элемент “сумма по модулю 2” и элемент “исключающее ИЛИ”. Схема (рис. 1) имеет два входа а и b для двух слагаемых и один выход S для суммы. Работу её отражает таблица истинности 1 (табл. 1), а соответствующее уравнение имеет вид
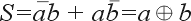
| (1) |
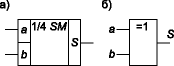 Рис. 1
Рис. 1
|
Таблица 1
| a | b | S |
Данный элемент выпускается в виде интегральных схем (ИС) типа ЛП5 (серии 133, 155, 530, 531, 533, 555, 1531, 1533); ЛП12 (555); ЛП107 (100, 500, 1500); ЛП2 (561, 564); ЛП14 (1561) и т. п.
Реализуем четвертьсумматор в базисах И-НЕ, ИЛИ-НЕ и с использованием только одного инвертора, для чего преобразуем уравнение (1):
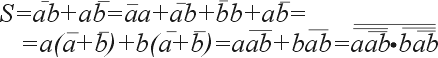
| (2) |
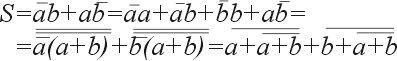
| (3) |
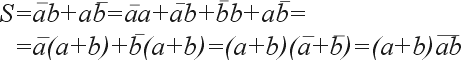
| (4) |
Схемы, полученные по уравнениям (2)–(4), приведены на рис. 2.
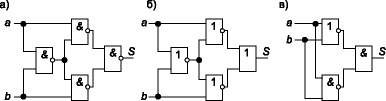
Рис. 2
Полусумматор
Полусумматор (рис. 3) имеет два входа a и b для двух слагаемых и два выхода: S — сумма, P — перенос. Обозначением полусумматора служат буквы HS (half sum — полусумма). Работу его отражает таблица истинности 2 (табл. 2), а соответствующие уравнения имеют вид:
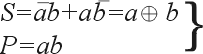
| (5) |
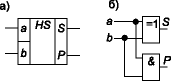 Рис. 3
Рис. 3
|
Таблица 2
| a | b | P | S |
Из уравнений (5) следует, что для реализации полусумматора требуется один элемент “исключающее ИЛИ” и один двухвходовый вентиль И (рис. 3б).
Дата добавления: 2016-02-20; просмотров: 2266;
