Определение отметки свободной поверхности воды в сборном колодце
 Колодец соединен с источником водоснабжения (рекой, водоприемным ковшом, шахтным колодцем – в зависимости от варианта задания) водозаборной линией (самотечной линией, дюкером или сифоном) так, что они представляют собой два сообщающихся резервуара. По водозаборной линии вода движется самотеком в результате понижения уровня воды в колодце при работе насоса.
Колодец соединен с источником водоснабжения (рекой, водоприемным ковшом, шахтным колодцем – в зависимости от варианта задания) водозаборной линией (самотечной линией, дюкером или сифоном) так, что они представляют собой два сообщающихся резервуара. По водозаборной линии вода движется самотеком в результате понижения уровня воды в колодце при работе насоса.



 А p0 Б
А p0 Б
 p2
p2

 1 2
1 2
 Z0 Z1
Z0 Z1
 плоскость сравнения Z2
плоскость сравнения Z2
Рис.4.1. Самотечная линия
Рассмотрим последовательно схемы водозаборных линий для каждого варианта задания.
Для варианта А – это самотечная линия, рис.4.1.
Для определения отметки поверхности воды в гидравлических системах используют уравнение Д. Бернулли. В данном случае это уравнение удобно записать применительно к двум сечениям потока, совпадающим с уровнями воды в источнике водоснабжения «А» и в колодце «Б». Плоскость сравнения удобно совместить с плоскостью, от которой ведется отсчет всех отметок в задании [3].
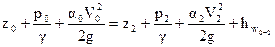 , (4.3)
, (4.3)
где в общем случае z - геометрическая высота расположения центра тяжести рассматриваемого сечения над плоскостью сравнения;
p - давление в рассматриваемом сечении потока;
g - удельный вес жидкости;
g – ускорение свободного падения;
V - средняя по сечению скорость потока;
a - коэффициент Кориолиса;
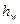 - потеря напора (удельной энергии жидкости) между рассматриваемыми сечениями.
- потеря напора (удельной энергии жидкости) между рассматриваемыми сечениями.
Искомая отметка свободной поверхности воды в колодце «Б» – z2. Находят ее, выразив из уравнения Д. Бернулли
 , (4.4)
, (4.4)
здесь z0 - отметка уровня воды в реке «А» – известна (см. исходные данные, прил.6);
p0 - давление на свободную поверхность воды в реке «А» равно атмосферному (p0=pа);
p2 - давление на свободную поверхность воды в колодце «Б» равно атмосферному (p2=pа);
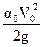 и
и 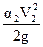 - скоростные напоры в рассматриваемых сечениях потока. Поскольку скорости движения в источнике водоснабжения и колодце обычно бывают невелики, величинами скоростных напоров в данном случае можно пренебречь
- скоростные напоры в рассматриваемых сечениях потока. Поскольку скорости движения в источнике водоснабжения и колодце обычно бывают невелики, величинами скоростных напоров в данном случае можно пренебречь 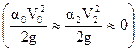 .
.
С учетом вышесказанного 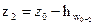 . (4.5)
. (4.5)
Таким образом, задача сводится собственно к определению 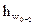 - суммарных потерь напора в трубопроводе, соединяющем источник водоснабжения с колодцем, т.е. в самотечной линии для варианта А.
- суммарных потерь напора в трубопроводе, соединяющем источник водоснабжения с колодцем, т.е. в самотечной линии для варианта А.
Так как самотечную линию (дюкер, сифон) относят обычно к гидравлически коротким трубопроводам, то суммарную (общую) потерю напора в них определяют с использованием принципа наложения потерь, см. (2.1), (2.2), (2.3) и (3.1)
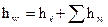 . (4.6)
. (4.6)
Потери напора по длине трубопровода 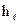 могут быть найдены по формуле
могут быть найдены по формуле
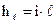 , (4.7)
, (4.7)
где i - гидравлический уклон, значение которого в соответствии с выбранным диаметром трубы и скоростью течения воды в ней определяют для водозаборной линии в п. 4.1.;
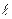 - длина трубы (самотечной линии, дюкера, сифона).
- длина трубы (самотечной линии, дюкера, сифона).
Суммарные местные потери напора 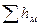 определяют с учетом всех видов местных сопротивлений, указанных в задании для данного трубопровода. Так для самотечной линии – это предохранительная сетка и сопротивление на выходе из трубы.
определяют с учетом всех видов местных сопротивлений, указанных в задании для данного трубопровода. Так для самотечной линии – это предохранительная сетка и сопротивление на выходе из трубы.
Таким образом 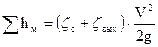 , (4.8)
, (4.8)
где  и
и 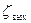 - коэффициенты местных сопротивлений сетки и на выходе из трубы (указаны в задании, прил.6);
- коэффициенты местных сопротивлений сетки и на выходе из трубы (указаны в задании, прил.6);
V – скорость течения воды в трубе, подсчитывают по формуле (4.2), п.4.1.
Подставляя найденное с помощью формул (4.6), (4.7), (4.8) значение потерь напора в уравнение (4.5) и решая его, определяют искомую отметку поверхности воды в колодце с точностью до 0,01 м.
В варианте Б водозаборная линия – это дюкер, рис.4.2.
 |




 А p0 Б
А p0 Б

 P7
P7

 1 2 5
1 2 5


 6
6

 3 4
3 4
Z0 Z1 Z3 Z6 Z7
 |
плоскость сравнения
Рис. 4.2. Дюкер
Для определения отметки свободной поверхности воды в колодце «Б» Z7 составляют уравнение Д. Бернулли для двух сечений потока, совпадающих с уровнями воды в источнике водоснабжения – водоприемном ковше «А» и в колодце «Б»
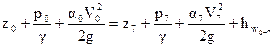 . (4.9)
. (4.9)
Так как p0=p7=pа; 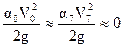 в связи с малостью скоростей течения в ковше и колодце, то
в связи с малостью скоростей течения в ковше и колодце, то
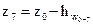 , (4.10)
, (4.10)
где z0 – отметка поверхности воды в ковше «А» (см. исходные данные, прил.6);
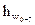 - суммарные потери напора в дюкере.
- суммарные потери напора в дюкере.
Суммарные потери напора в дюкере находят с помощью выражения (4.6). Потери напора по длине дюкера – с помощью (4.7).
Суммарные местные потери напора для дюкера
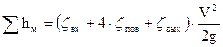 , (4.11)
, (4.11)
где 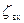 ,
, 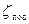 ,
, 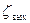 - коэффициенты местных сопротивлений на входе, повороте и выходе из дюкера (см. исходные данные, прил.6);
- коэффициенты местных сопротивлений на входе, повороте и выходе из дюкера (см. исходные данные, прил.6);
V – скорость течения воды в дюкере, определяют по формуле (4.2), п.4.1.
Подставляя найденные таким образом значения потерь напора в (4.10) определяют искомую отметку воды в колодце z7.
Вариант В. Водозаборная линия – сифон, рис. 4.3.
 Б
Б







 А p0
А p0


 p3
p3
 |
 Z
Z 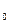
1 2 Z  Z
Z 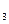
 | |||
 | |||
Z  плоскость сравнения
плоскость сравнения
 |
Рис. 4.3. Сифон для варианта В
Необходимо определить отметку свободной поверхности воды в колодце «Б» - Z3.
Составляют уравнение Д. Бернулли для двух сечений потока, совпадающих со свободной поверхностью воды в реке «А» и в колодце «Б».
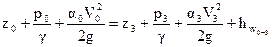 . (4.12)
. (4.12)
Так как p0=p3=pа ; 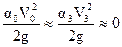 в связи с малостью скоростей течения в реке и колодце, то
в связи с малостью скоростей течения в реке и колодце, то
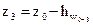 , (4.13)
, (4.13)
где z0 – отметка поверхности воды в реке «А», дана в задании, прил.6;
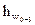 - суммарные потери напора в сифоне, определяют по (4.6).
- суммарные потери напора в сифоне, определяют по (4.6).
Потери напора по длине сифона находят с помощью (4.7).
Суммарные местные потери напора в сифоне
 , (4.14)
, (4.14)
где 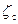 ,
, 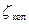 ,
, 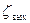 - коэффициенты местных сопротивлений сетки, колена и на выходе из сифона, указаны в задании;
- коэффициенты местных сопротивлений сетки, колена и на выходе из сифона, указаны в задании;
V – скорость течения воды в сифоне по формуле (4.2), п.4.1.
В варианте Г водозаборная линия состоит из двух одинаковых сифонов. Для определения отметки свободной поверхности воды Z3 в сборном колодце «В» достаточно рассмотреть работу одного из этих сифонов, рис. 4.4.


















 А В
А В
р1 р3
1 2
 Z3
Z3
Z1 Z2
 | |||
 |
плоскость сравнения
Рис. 4.4. Сифон для варианта Г
Составляют уравнение Д. Бернулли для двух сечений потока, совпадающих со свободной поверхностью воды в шахтном колодце «А» и сборном колодце «В»
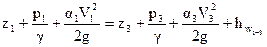 . (4.15)
. (4.15)
В связи с тем, что p1=p3=pа ; 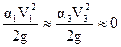 , так как скорости течения в обоих колодцах очень малы, то
, так как скорости течения в обоих колодцах очень малы, то
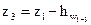 , (4.16)
, (4.16)
где z1 – отметка поверхности воды в колодце «А», см. исходные данные, прил.6;
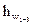 - суммарные потери напора в сифоне, определяют по (4.6).
- суммарные потери напора в сифоне, определяют по (4.6).
Потери напора по длине сифона находят с помощью (4.7).
Суммарные местные потери напора в сифоне
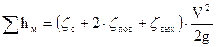 , (4.17)
, (4.17)
где 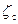 ,
, 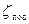 ,
, 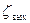 - коэффициенты местных сопротивлений сетки, поворота и на выходе из трубы, указаны в задании;
- коэффициенты местных сопротивлений сетки, поворота и на выходе из трубы, указаны в задании;
V – скорость течения воды в сифоне по формуле (4.2), п.4.1.
Дата добавления: 2016-02-16; просмотров: 934;
